数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学两个半径分别为 5 厘米和 3 厘米的圆相交于两点，且它们的圆心距为 4 厘米。求公共弦的长度。
已知
两个圆的半径分别为 5 厘米和 3 厘米。
两圆圆心之间的距离为 4 厘米。
求解
我们需要求出公共弦的长度。
解：
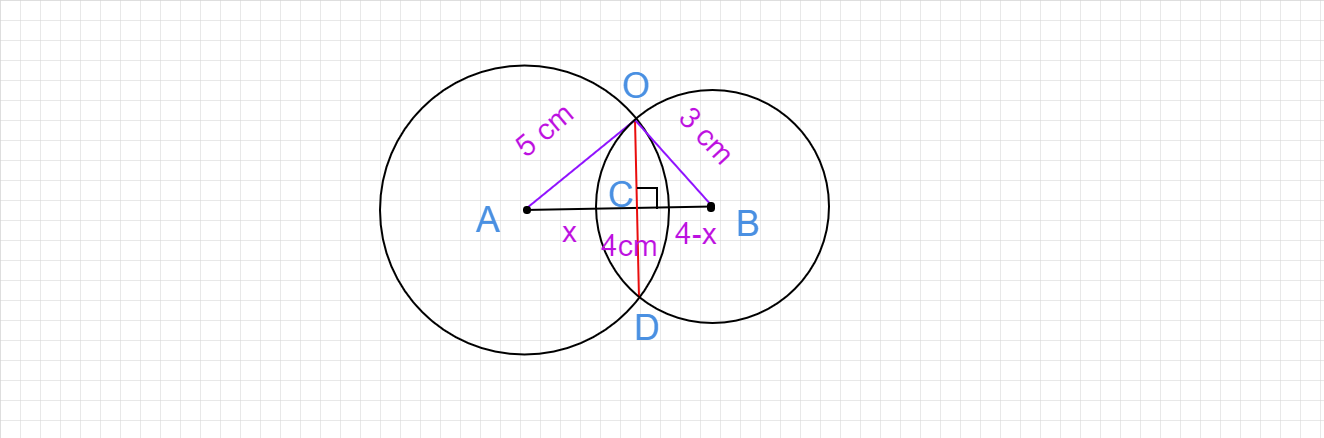
在上图中，$AO=5 cm, BO=3 cm$
$AB = 4 cm, AC = x, BC = 4-x$。
$OD$ 是两个圆的公共弦。
我们需要求出公共弦 $OD$ 的长度。
我们知道：
弦的垂直平分线经过圆心。
所以，$OC = CD$ 且 $\angle ACO =\angle BCO = 90°$。
在 $\triangle ACO$ 中，$AO^2 = AC^2+CO^2$
$5^2 =x^2+CO^2$
$CO^2 = 5^2-x^2$
$CO^2=25-x^2$.............(i)
在 $\triangle BCO$ 中，$BO^2 = BC^2+CO^2$
$3^2=(4-x)^2+CO^2$
$CO^2=3^2-(4-x)^2$
$CO^2 = 9-16+8x-x^2$.........(ii)
联立 (i) 和 (ii)，得到：
$25-x^2= 9-16+8x-x^2$
$25 = -7+8x$
$8x = 25+7$
$8x=32$
$x = \frac{32}{8}=4$
将 $x=4$ 代入 (i)，
$CO^2=25-4^2$
$CO^2=25-16$
$CO^2=9$
$CO=3$
我们知道，$CO=CD=3$。
$OD=OC+CD=3+3=6$
$OD=6 cm$。
因此，公共弦的长度为 6 厘米。
251 次浏览
