使用Excel Solver进行优化

求解器 (Solver) 是一个Microsoft Excel加载项程序，可用于假设分析中的优化。

根据O'Brien和Marakas的说法，优化分析是目标求解分析的一个更复杂的扩展。它不是为变量设置特定的目标值，而是要在某些约束条件下找到一个或多个目标变量的最佳值。然后，在满足指定约束条件的情况下，重复更改一个或多个其他变量，直到找到目标变量的最佳值。

在Excel中，您可以使用求解器 (Solver) 为一个称为目标单元格的单元格中的公式找到最优值（最大值或最小值，或某个特定值），该单元格受工作表上其他公式单元格的值的某些约束或限制。

这意味着求解器与一组称为决策变量的单元格一起工作，这些单元格用于计算目标单元格和约束单元格中的公式。求解器调整决策变量单元格中的值以满足约束单元格的限制并产生目标单元格所需的计算结果。

您可以使用求解器来找到各种问题的最优解，例如：

确定制药厂的每月产品组合，以最大化盈利能力。
安排组织中的员工。
解决运输问题。
财务计划和预算。

激活求解器加载项

在使用求解器解决问题之前，请确保已在Excel中激活求解器加载项，方法如下：

单击功能区上的“数据”选项卡。求解器命令应显示在“分析”组中，如下所示。

如果您找不到求解器命令，请按以下步骤激活它：

单击“文件”选项卡。
在左侧窗格中单击“选项”。将出现“Excel选项”对话框。
在左侧窗格中单击“加载项”。
在“管理”框中选择“Excel加载项”，然后单击“转到”。

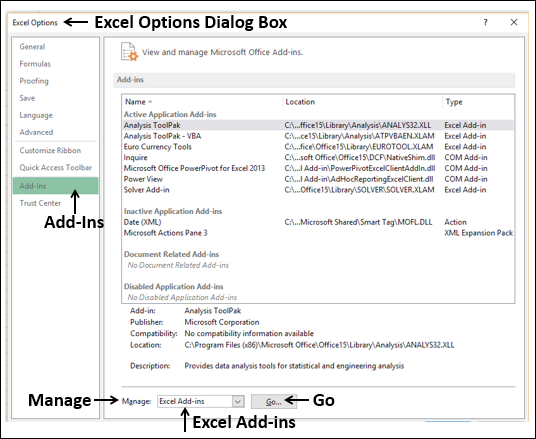
将出现“加载项”对话框。选中求解器加载项，然后单击“确定”。现在，您应该能够在功能区上的“数据”选项卡下找到求解器命令。

求解器使用的求解方法

根据问题的类型，您可以从Excel求解器支持的以下三种求解方法中选择一种：

线性规划单纯形法 (LP Simplex)

用于线性问题。在以下情况下，求解器模型是线性的：

目标单元格是通过将（可更改单元格）*（常数）形式的项加在一起计算的。
每个约束都满足线性模型要求。这意味着每个约束都是通过将（可更改单元格）*（常数）形式的项加在一起并将其与常数进行比较来计算的。

广义约简梯度 (GRG) 非线性

用于平滑的非线性问题。如果目标单元格、任何约束或两者都包含对不是（可更改单元格）*（常数）形式的可更改单元格的引用，则您具有非线性模型。

进化算法 (Evolutionary)

了解求解器评估

求解器需要以下参数：

决策变量单元格
约束单元格
目标单元格
求解方法

求解器评估基于以下内容：

决策变量单元格中的值受约束单元格中的值限制。
目标单元格中值的计算包括决策变量单元格中的值。
求解器使用所选的求解方法得出目标单元格中的最优值。

定义问题

假设您正在分析一家生产和销售某产品的公司的利润。您需要确定未来两个季度在广告上可以花费的金额，前提是最高为20,000。每个季度的广告水平会影响以下方面：

销售数量，间接决定销售收入。
相关费用，以及
利润。

您可以继续将问题定义为：

找到单位成本。
找到每单位广告成本。
找到单位价格。

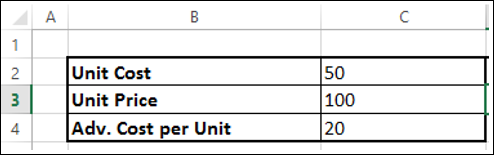
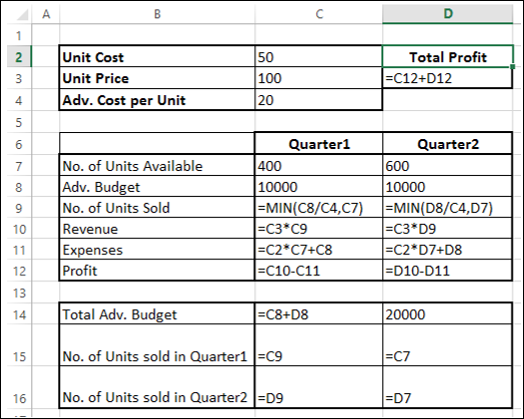
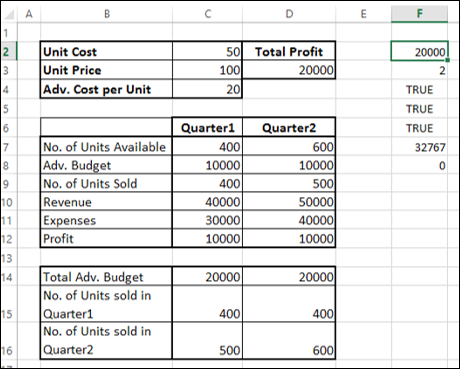
接下来，设置如下所示的所需计算的单元格。

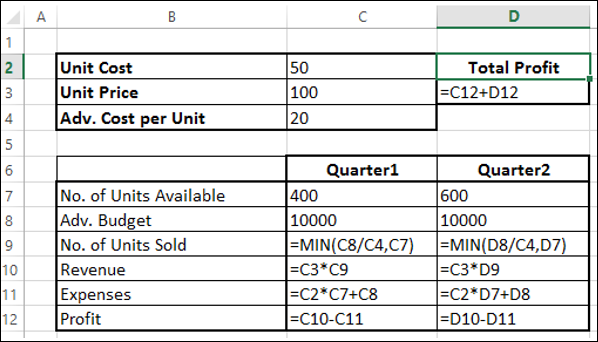
如您所见，计算结果针对的是正在考虑的第1季度和第2季度，包括：

第1季度的可售单位数为400，第2季度的可售单位数为600（单元格 - C7和D7）。
广告预算的初始值为每个季度10000（单元格 - C8和D8）。
销售数量取决于每单位广告成本，因此等于该季度的预算/每单位广告成本。请注意，我们使用了MIN函数来确保销售数量<=可售单位数。（单元格 - C9和D9）。
收入计算为单位价格*销售数量（单元格 - C10和D10）。
费用计算为单位成本*可售单位数+该季度的广告成本（单元格 - C11和D12）。
利润等于收入-费用（单元格C12和D12）。
总利润等于第1季度的利润+第2季度的利润（单元格 - D3）。

接下来，您可以如下设置求解器的参数：

如您所见，求解器的参数为：

目标单元格是D3，其中包含您要最大化的总利润。
决策变量单元格是C8和D8，其中包含两个季度（第1季度和第2季度）的预算。
有三个约束单元格 - C14、C15和C16。
- 包含总预算的单元格C14设置为20000的约束（单元格D14）。
- 包含第1季度销售数量的单元格C15设置为<=第1季度可售单位数的约束（单元格D15）。
- 包含第2季度销售数量的单元格C16设置为<=第2季度可售单位数的约束（单元格D16）。

解决问题

下一步是使用求解器找到解决方案，方法如下：

步骤1 - 转到功能区上的“数据”>“分析”>“求解器”。将出现“求解参数”对话框。

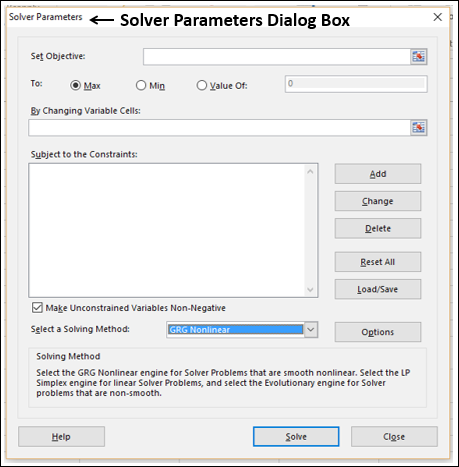
步骤2 - 在“设置目标单元格”框中，选择单元格D3。

步骤3 - 选择“最大化”。

步骤4 - 在“通过更改可变单元格”框中选择范围C8:D8。

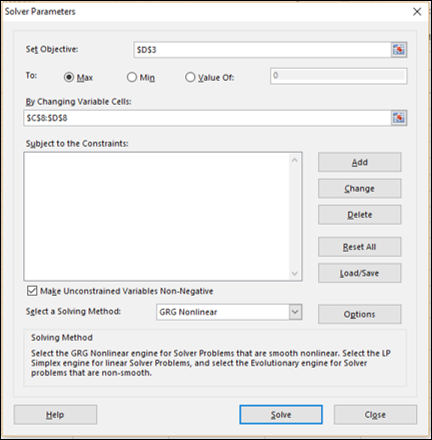
步骤5 - 接下来，单击“添加”按钮以添加您已识别的三个约束。

步骤6 - 将出现“添加约束”对话框。如下设置总预算的约束，然后单击“添加”。

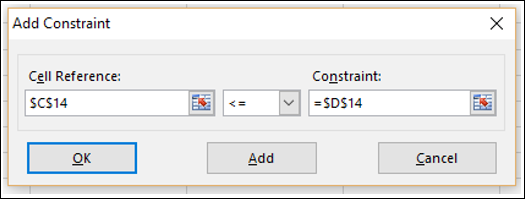
步骤7 - 如下设置第1季度总销售数量的约束，然后单击“添加”。

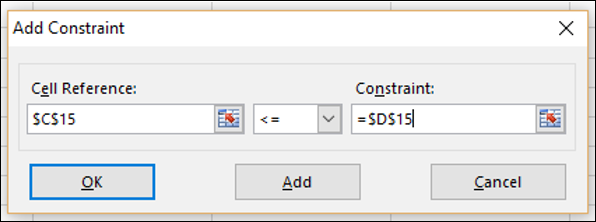
步骤8 - 如下设置第2季度总销售数量的约束，然后单击“确定”。

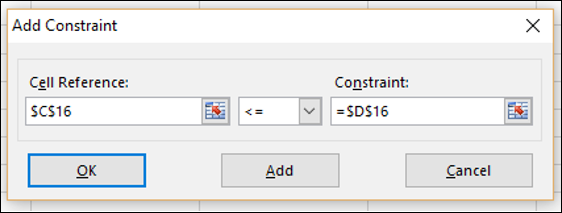
“求解参数”对话框出现，其中在“受约束条件”框中添加了三个约束。

步骤9 - 在“选择求解方法”框中，选择“线性规划单纯形法”。

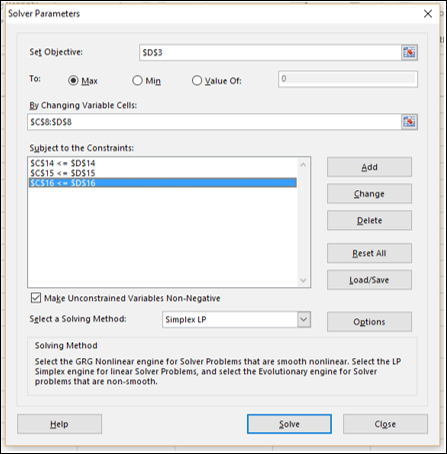
步骤10 - 单击“求解”按钮。将出现“求解结果”对话框。选择“保持求解器解”，然后单击“确定”。

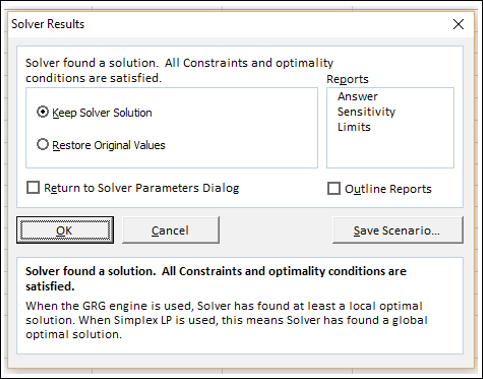
结果将显示在您的工作表中。

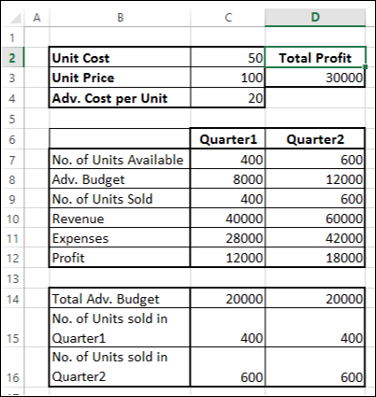
如您所见，在给定约束条件下产生最大总利润的最优解如下：

总利润 - 30000。
第1季度广告预算 - 8000。
第2季度广告预算 - 12000。

逐步浏览求解器试用解

您可以逐步浏览求解器试用解，查看迭代结果。

步骤1 - 在“求解参数”对话框中单击“选项”按钮。

将出现“选项”对话框。

步骤2 - 选中“显示迭代结果”框，然后单击“确定”。

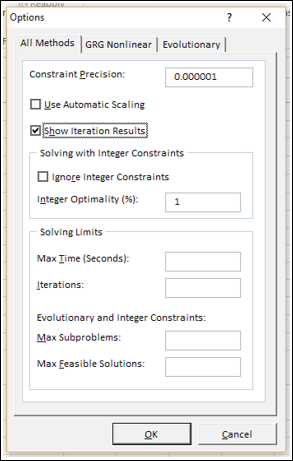
步骤3 - 将出现“求解参数”对话框。单击“求解”。

步骤4 - 将出现“显示试用解”对话框，显示消息 - “求解器已暂停，当前解值显示在工作表上”。

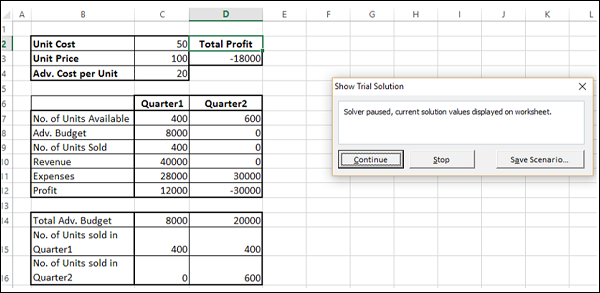
如您所见，当前迭代值显示在您的工作单元格中。您可以停止求解器接受当前结果，也可以继续使用求解器在后续步骤中查找解。

步骤5 - 单击“继续”。

在每个步骤中都会出现“显示试用解”对话框，最后在找到最优解后，将出现“求解结果”对话框。您的工作表在每个步骤中都会更新，最后显示结果值。

保存求解器选择

对于使用求解器解决的问题，您有以下保存选项：

您可以通过保存工作簿将“求解参数”对话框中的上次选择与工作表一起保存。
工作簿中的每个工作表都可以有自己的求解器选择，并且在保存工作簿时，所有这些选择都将被保存。
您还可以在一个工作表中定义多个问题，每个问题都有自己的求解器选择。在这种情况下，您可以使用“求解参数”对话框中的“加载/保存”分别加载和保存问题。
- 单击“加载/保存”按钮。将出现“加载/保存”对话框。
- 要保存问题模型，请输入要放置问题模型的垂直空单元格范围的第一个单元格的引用。单击“保存”。

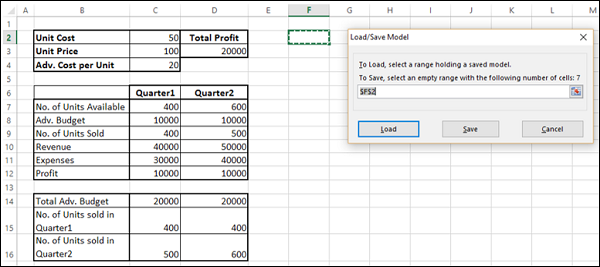
问题模型（求解器参数集）从您指定为参考的单元格开始显示。

要加载问题模型，请输入包含问题模型的整个单元格范围的引用。然后，单击“加载”按钮。

打印页面