数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律对于下列问题，建立二元一次方程组，并用任意代数方法求解
(i) 某寄宿学校的月住宿费包含固定部分和根据就餐天数计算的部分。学生A就餐20天，需支付1000卢比的住宿费；学生B就餐26天，需支付1180卢比的住宿费。求固定费用和每天的就餐费用。
(ii) 一个分数，如果分子减去1，则分数变为$\frac{1}{3}$；如果分母加上8，则分数变为$\frac{1}{4}$。求这个分数。
(iii) 亚什在一项测试中得了40分，每答对一题得3分，每答错一题扣1分。如果每答对一题得4分，每答错一题扣2分，那么亚什将得到50分。测试中共有多少道题？
(iv) A地和B地相距100公里，在同一条公路上。一辆汽车从A地出发，另一辆汽车从B地同时出发。如果两车沿相同方向行驶，速度不同，则5小时后相遇；如果两车相向行驶，则1小时后相遇。求这两辆汽车的速度。
(v) 如果一个矩形的长减少5个单位，宽增加3个单位，则面积减少9平方单位。如果长增加3个单位，宽增加2个单位，则面积增加67平方单位。求矩形的长和宽。
待办事项
我们需要建立二元一次方程组，并用任意代数方法求解。
解答：(i) 设固定费用和每天的就餐费用分别为$x$和$y$。
当学生A就餐20天时，需支付1000卢比的住宿费。
这意味着，
$x + 20y = 1000$.....(i)
当学生B就餐26天时，需支付1180卢比的住宿费。
这意味着，
$x + 26y = 1180$.....(ii)
用方程(ii)减去方程(i)，得到：
$(x+26y)-(x+20y)=1180-1000$
$x-x+26y-20y=180$
$6y=180$
$y=\frac{180}{6}$
$y=30$
将$y=30$代入方程(i)，得到：
$x+20(30)=1000$
$x+600=1000$
$x=1000-600$
$x=400$
固定费用为400卢比，每天的就餐费用为30卢比。
(ii) 设原分数的分子和分母分别为$x$和$y$。
原分数$=\frac{x}{y}$
如果分子减去1，则分数变为$\frac{1}{3}$。
这意味着，
新分数$=\frac{x-1}{y}$
根据题意，
$\frac{x-1}{y}=\frac{1}{3}$
$3(x-1)=1(y)$ (交叉相乘)
$3x-3=y$
$y=3x-3$.....(i)
如果分母加上8，则分数变为$\frac{1}{4}$。
这意味着，
$\frac{x}{y+8}=\frac{1}{4}$
$4(x)=1(y+8)$ (交叉相乘)
$4x=y+8$
$4x-y-8=0$
$4x-(3x-3)-8=0$ (由(i)得)
$4x-3x+3-8=0$
$x-5=0$
$x=5$
$\Rightarrow y=3(5)-3$
$y=15-3$
$y=12$
因此，原分数为$\frac{5}{12}$。
(iii) 设答对的题数为$x$，答错的题数为$y$。
这意味着，
总题数$=x+y$。
在第一种情况下，每答对一题得3分，每答错一题扣1分。
根据题意，
$40=3x+(-1)y$
$y=3x-40$.....(i)
在第二种情况下，每答对一题得4分，每答错一题扣2分。
根据题意，
$50=4x+(-2)y$
$2y=4x-50$
$2y=2(2x-25)$
$y=2x-25$.....(ii)
由(i)和(ii)得，
$3x-40=2x-25$
$3x-2x=40-25$
$x=15$
这意味着，
$y=2(15)-25$
$y=30-25$
$y=5$
$\Rightarrow x+y=15+5=20$
测试中共有20道题。
(iv) 我们知道，
距离$=$ 速度 $\times$ 时间。
A地和B地之间的距离$= 100\ 公里$。
设从A地出发的第一辆汽车的速度为$x\ 公里/小时$，从B地出发的第二辆汽车的速度为$y\ 公里/小时$。
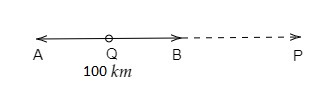
设当两车沿相同方向行驶时在P点相遇，当两车相向行驶时在Q点相遇。
当两车沿相同方向行驶时，5小时后相遇。
第一辆汽车在5小时内行驶的距离$AP= 5\times x\ 公里=5x\ 公里$。
第二辆汽车在5小时内行驶的距离$BP= 5\times y\ 公里=5y\ 公里$。
$AP-BP=100$
$5x-5y=100$
$5(x-y)=5\times20$
$x-y=20$.....(i)
当两车相向行驶时，1小时后相遇。
第一辆汽车在1小时内行驶的距离$AQ= 1\times x\ 公里=x\ 公里$。
第二辆汽车在1小时内行驶的距离$BQ= 1\times y\ 公里=y\ 公里$。
$AQ+BQ=AB$
$x + y = 100$….(ii)
将方程(i)和(ii)相加，得到：
$x-y+x+y=20+100$
$2x = 120$
$x = \frac{120}{2}$
$x=60$
将$x=60$代入方程(ii)，得到：
$60+y=100$
$y = 100-60$
$y = 40$
因此，第一辆汽车的速度为$60\ 公里/小时$，第二辆汽车的速度为$40\ 公里/小时$。
(v) 设矩形的原长为$l$，原宽为$b$。
原矩形的面积$=lb$。
在第一种情况下，长减少5个单位，宽增加3个单位，矩形的面积减少9平方单位。
新的长$=l-5$
新的宽$=b+3$
新矩形的面积$=(l-5)(b+3)$平方单位
根据题意，
$(l-5)(b+3)=lb-9$
$lb-5b+3l-15=lb-9$
$3l-5b=15-9$
$3l-5b=6$.....(i)
在第二种情况下，长增加3个单位，宽增加2个单位，面积增加67平方单位。
新的长$=l+3$
新的宽$=b+2$
新矩形的面积$=(l+3)(b+2)$平方单位
根据题意，
$(l+3)(b+2)=lb+67$
$lb+2l+3b+6=lb+67$
$2l+3b=67-6$
$2l+3b=61$.....(ii)
用$3\times(ii)$减去$2\times(i)$，得到：
$3(2l+3b)-2(3l-5b)=3(61)-2(6)$
$6l-6l+9b+10b=183-12$
$19b=171$
$b=\frac{171}{19}$
$b=9$
$2l+3(9)=61$ (由(ii)得)
$2l=61-27$
$2l=34$
$l=\frac{34}{2}$
$l=17$
矩形的长为17个单位，宽为9个单位。
浏览量：53
