Loading [MathJax]/jax/output/HTML-CSS/jax.js

构造一个与已知三角形 AB'C' 相似的三角形 ABC，其边长等于三角形 AB'C' 对应边长的 $\frac{5}{3}$ （即比例因子为 $\frac{5}{3}$ ）。

学术数学 NCERT 10 年级

待办事项：

构造一个与已知三角形 AB'C' 相似的三角形 ABC，其边长等于三角形 AB'C' 对应边长的

$\frac{5}{3}$ 。

解答

让我们构造一个

$\vartriangle AB'C'$ ，其中

$C'A= 6\ cm$ ，

$AB'= 3\ cm$ 且

$\angle B'AC'= 45^{o}$ 。

我们需要构造一个三角形 ABC，其边长等于三角形 AB'C' 对应边长的

$\frac{5}{3}$ 。

作图步骤

1. 画

$AB'=3\ cm$ 。以 A 为圆心，画

$\angle B'AC'= 45^{o}$ 。连接 B'C'。这样就形成了 AB'C'。

2. 画 AX 使得

$\angle B'AX$ 为锐角。

3. 截取 5 个相等的弧，使得

$AA_{1}=A_{1}A_{2}=A_{2}A_{3}=A_{3}A_{4}=A_{4}A_{5}$

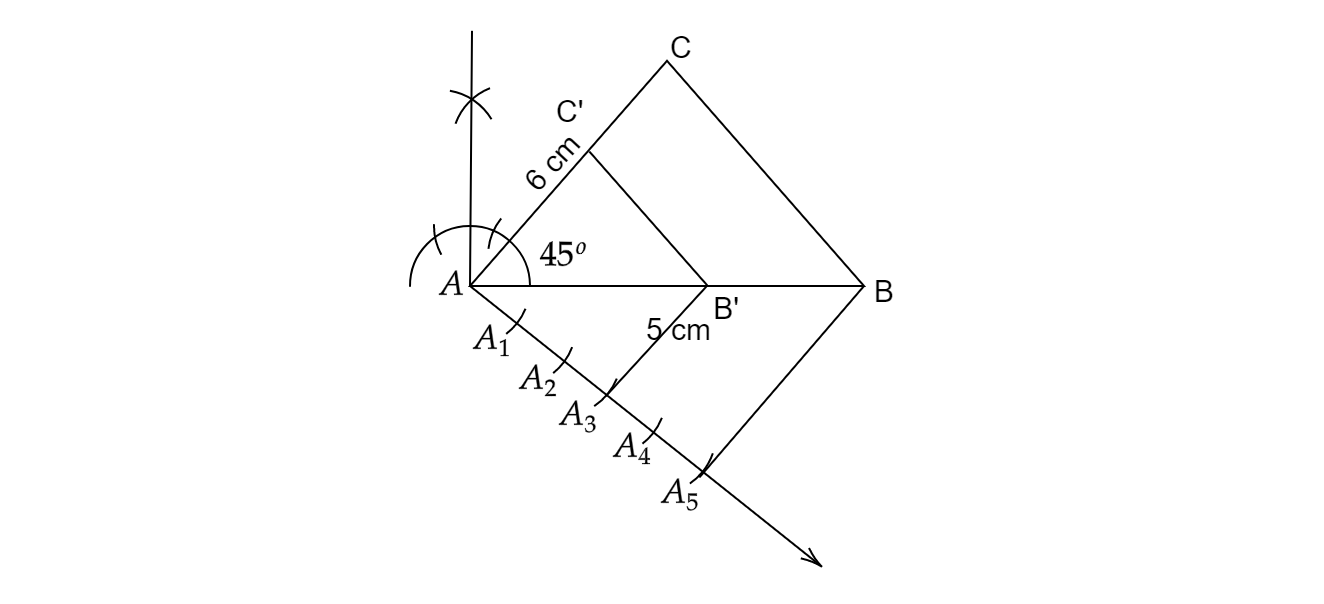
4. 连接

$A_{5}$ 到

$B'$ ，并过

$A_{5}$ 画一条平行于

$A_{3}B'$ 的直线，该直线交 AB' 于 B。

这里，

$AB=\frac{5}{3}AB'$ 。

现在，过

$B$ 画一条平行于

$B'C'$ 的直线，该直线交 AC' 的延长线于

$C$ 。

这里，

$BC=\frac{5}{3}B'C'$ 且

$AC=\frac{5}{3}AC'$

因此，

$\vartriangle ABC$ 是所需的三角形。

教程点

更新于: 2022-10-10

45 次浏览

开启你的职业生涯

通过完成课程获得认证

广告