在下图中，$ABCD、DCFE$ 和 $ABFE$ 是平行四边形。证明 \( \operatorname{ar}(\mathrm{ADE})=\operatorname{ar}(\mathrm{BCF}) \)。

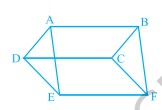
已知

$ABCD、DCFE$ 和 $ABFE$ 是平行四边形。

需要证明

我们需要证明 $ar(\triangle ADE) = ar(\triangle BCF)$。

解答

$ABCD$ 是平行四边形。

这意味着：

$AD = BC$

同样地：

在平行四边形 $ABEF$ 中：

$AE = BF$

在平行四边形 $CDEF$ 中：

$DE = CF$

在 $\triangle ADE$ 和 $\triangle BCF$ 中：

$AD = BC$

$DE = CF$

$AE = BF$

因此，根据SSS公理：

$\triangle ADE \cong \triangle BCF$

这意味着：

$ar(\triangle ADE) = ar(\triangle BCF)$ (全等三角形的面积相等)

证毕。

Tutorialspoint

更新于：2022年10月10日

浏览量：32

开启您的职业生涯

完成课程获得认证

开始学习