
模拟通信 - AM 调制器
本章我们将讨论产生调幅波的调制器。以下两种调制器可以产生AM波。
- 平方律调制器
- 开关调制器
平方律调制器
以下是平方律调制器的框图
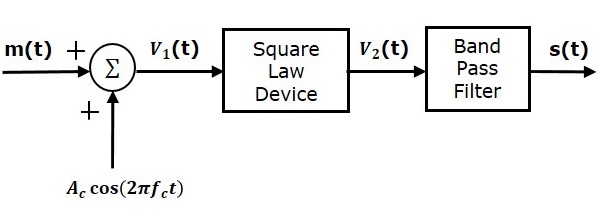
设调制信号和载波信号分别表示为$m\left ( t \right )$和$A\cos\left ( 2\pi f_ct\right )$。这两个信号作为输入信号施加到加法器模块。该加法器模块产生一个输出,它是调制信号和载波信号的和。数学上,我们可以写成
$$V_1(t)=m\left ( t \right )+A_c\cos\left ( 2 \pi f_ct \right )$$
该信号$V_1(t)$作为输入信号施加到非线性器件(如二极管)。二极管的特性与平方律密切相关。
$V_2(t)=k_1V_1\left ( t \right )+k_2V_1^2\left ( t \right )$(公式 1)
其中,$k_1$和$k_2$是常数。
将$V_1\left(t \right)$代入公式 1
$$V_2\left (t\right ) = k_1\left [ m\left ( t \right ) + A_c \cos \left ( 2 \pi f_ct \right ) \right ] + k_2\left [ m\left ( t \right ) + A_c \cos\left ( 2 \pi f_ct \right ) \right ]^2$$
$\Rightarrow V_2\left (t\right ) = k_1 m\left ( t \right ) +k_1 A_c \cos \left ( 2 \pi f_ct \right ) +k_2 m^2\left ( t \right ) +$
$ k_2A_c^2 \cos^2\left ( 2 \pi f_ct \right )+2k_2m\left ( t \right )A_c \cos\left ( 2 \pi f_ct \right )$
$\Rightarrow V_2\left (t\right ) = k_1 m\left ( t \right ) +k_2 m^2\left ( t \right ) +k_2 A^2_c \cos^2 \left ( 2 \pi f_ct \right ) +$
$k_1A_c\left [ 1+\left ( \frac{2k_2}{k_1} \right )m\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$
上式最后一项表示所需的AM波,前三项是不需要的。因此,借助带通滤波器,我们可以只让AM波通过并消除前三项。
因此,平方律调制器的输出为
$$s\left ( t \right )=k_1A_c\left [1+\left ( \frac{2k_2}{k_1} \right ) m\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
AM波的标准方程为
$$s\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos \left (2 \pi f_ct \right )$$
其中,$K_a$是幅度灵敏度
通过将平方律调制器的输出与AM波的标准方程进行比较,我们可以得到比例因子为$k_1$,幅度灵敏度$k_a$为$\frac{2k_2}{k1}$。
开关调制器
以下是开关调制器的框图。
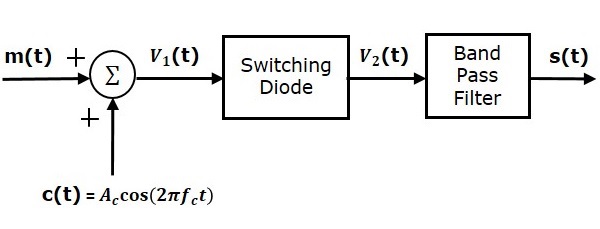
开关调制器类似于平方律调制器。唯一的区别在于,在平方律调制器中,二极管工作在非线性模式,而在开关调制器中,二极管必须作为理想开关工作。
设调制信号和载波信号分别表示为$m\left ( t \right )$和$c\left ( t \right )= A_c \cos\left ( 2\pi f_ct \right )$。这两个信号作为输入信号施加到加法器模块。加法器模块产生一个输出,它是调制信号和载波信号的和。数学上,我们可以写成
$$V_1\left ( t \right )=m\left ( t \right )+c\left ( t \right )= m\left ( t \right )+A_c \cos\left ( 2 \pi f_ct \right )$$
该信号$V_1\left ( t \right )$作为二极管的输入信号。假设调制信号的幅度与载波信号$A_c$的幅度相比非常小。因此,二极管的导通和截止动作由载波信号$c\left ( t \right )$控制。这意味着,当$c\left ( t \right )> 0$时,二极管将正向偏置;当$c\left ( t \right )< 0$时,二极管将反向偏置。
因此,二极管的输出为
$$V_2 \left ( t \right )=\left\{\begin{matrix} V_1\left ( t \right )& if &c\left ( t \right )>0 \\ 0& if & c\left ( t \right )<0 \end{matrix}\right.$$
我们可以将其近似为
$V_2\left ( t \right ) = V_1\left ( t \right )x\left ( t \right )$(公式 2)
其中,$x\left ( t \right )$是周期为$T=\frac{1}{f_c}$的周期脉冲序列。

该周期脉冲序列的傅里叶级数表示为
$$x\left ( t \right )=\frac{1}{2}+\frac{2}{\pi }\sum_{n=1}^{\infty}\frac{\left ( -1 \right )^n-1}{2n-1} \cos\left (2 \pi \left ( 2n-1 \right ) f_ct \right )$$
$$\Rightarrow x\left ( t \right )=\frac{1}{2}+\frac{2}{\pi} \cos\left ( 2 \pi f_ct \right )-\frac{2}{3\pi } \cos\left ( 6 \pi f_ct \right ) +....$$
将$V_1\left ( t \right )$和$x\left ( t \right )$的值代入公式 2。
$V_2\left ( t \right )=\left [ m\left ( t \right )+A_c \cos\left ( 2 \pi f_ct \right ) \right ] \left [ \frac{1}{2} + \frac{2}{\pi} \cos \left ( 2 \pi f_ct \right )-\frac{2}{3\pi} \cos\left ( 6 \pi f_ct \right )+.....\right ]$
$V_2\left ( t \right )=\frac{m\left ( t \right )}{2}+\frac{A_c}{2} \cos\left ( 2 \pi f_ct \right )+\frac{2m\left ( t \right )}{\pi} \cos\left ( 2 \pi f_ct \right ) +\frac{2A_c}{\pi} \cos^2\left ( 2 \pi f_ct \right )-$
$\frac{2m\left ( t \right )}{3\pi} \cos\left ( 6 \pi f_ct \right )-\frac{2A_c}{3\pi}\cos \left ( 2 \pi f_ct \right ) \cos\left ( 6 \pi f_ct \right )+..... $
$V_2\left ( t \right )=\frac{A_c}{2}\left ( 1+\left ( \frac{4}{\pi A_c} \right )m\left ( t \right ) \right ) \cos\left ( 2 \pi f_ct \right ) + \frac{m\left ( t \right )}{2}+\frac{2A_c}{\pi} \cos^2\left ( 2 \pi f_ct \right )-$
$\frac{2m\left ( t \right )}{3 \pi} \cos\left ( 6 \pi f_ct \right )-\frac{2A_c}{3\pi} \cos\left ( 2 \pi f_ct \right ) \cos\left ( 6 \pi f_ct \right )+.....$
上式第一项表示所需的AM波,其余项是不需要的项。因此,借助带通滤波器,我们可以只让AM波通过并消除其余项。
因此,开关调制器的输出为
$$s\left ( t \right )=\frac{A_c}{2}\left ( 1+\left ( \frac{4}{\pi A_c} \right ) m\left ( t \right )\right ) \cos\left ( 2 \pi f_ct \right )$$
我们知道AM波的标准方程为
$$s\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
其中,$k_a$是幅度灵敏度。
通过将开关调制器的输出与AM波的标准方程进行比较,我们可以得到比例因子为0.5,幅度灵敏度$k_a$为$\frac{4}{\pi A_c}$。