
DSBSC解调器
从DSBSC波中提取原始消息信号的过程称为DSBSC的检测或解调。以下解调器(检测器)用于解调DSBSC波。
- 相干检测器
- 科斯塔斯环路
相干检测器
这里,使用相同的载波信号(用于产生DSBSC信号)来检测消息信号。因此,这个检测过程称为相干或同步检测。以下是相干检测器的框图。
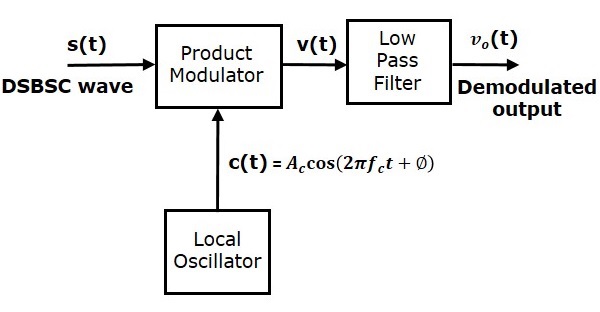
在这个过程中,可以通过将DSBSC波与具有与DSBSC调制中使用的载波相同频率和相位的载波相乘来提取消息信号。然后将得到的信号通过低通滤波器。该滤波器的输出是所需的消息信号。
设DSBSC波为
$$s\left ( t \right )= A_c \cos\left ( 2 \pi f_ct \right )m \left ( t \right )$$
局部振荡器的输出为
$$c\left ( t \right )= A_c \cos\left ( 2 \pi f_ct+ \phi \right )$$
其中,$\phi$是局部振荡器信号与用于DSBSC调制的载波信号之间的相位差。
从图中,我们可以将乘法器的输出写为
$$v\left ( t \right )=s\left ( t \right )c\left ( t \right )$$
将$s\left ( t \right )$和$c\left ( t \right )$的值代入上述方程。
$$\Rightarrow v\left ( t \right )=A_c \cos \left ( 2 \pi f_ct \right )m\left ( t \right )A_c \cos \left ( 2 \pi f_ct + \phi \right )$$
$={A_{c}}^{2} \cos \left ( 2 \pi f_ct \right ) \cos \left ( 2 \pi f_ct + \phi \right )m\left ( t \right )$$
$=\frac{{A_{c}}^{2}}{2}\left [ \cos\left ( 4 \pi f_ct+ \phi \right )+ \cos \phi \right ]m\left ( t \right )$$
$$v\left ( t \right )=\frac{{A_{c}}^{2}}{2} \cos\phi m\left ( t \right )+\frac{{A_{c}}^{2}}{2} \cos \left ( 4 \pi f_ct+ \phi \right )m\left ( t \right )$$
在上式中,第一项是消息信号的缩放版本。可以通过将上述信号通过低通滤波器来提取它。
因此,低通滤波器的输出为
$$v_0(t)=\frac{{A_{c}}^{2}}{2} \cos \phi m \left ( t \right )$$
当$\phi=0^0$时,解调信号幅度最大。这就是为什么局部振荡器信号和载波信号应该同相,即这两个信号之间不应该有任何相位差。
当$\phi=\pm 90^0$时,解调信号幅度为零。这种效应称为正交零效应。
科斯塔斯环路
科斯塔斯环路用于使载波信号(用于DSBSC调制)和局部产生的信号同相。以下是科斯塔斯环路的框图。
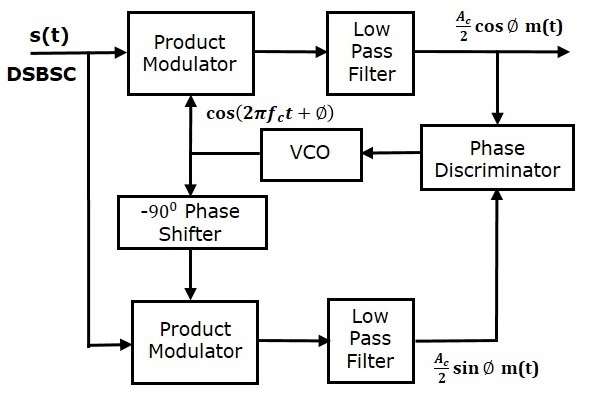
科斯塔斯环路由两个乘法器组成,它们具有公共输入$s\left ( t \right )$,它是DSBSC波。两个乘法器的另一个输入来自压控振荡器(VCO),其中一个乘法器具有$-90^0$的相移,如图所示。
我们知道DSBSC波的方程是
$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )m\left ( t \right )$$
设VCO的输出为
$$c_1\left ( t \right )=\cos\left ( 2 \pi f_ct + \phi\right )$$
VCO的这个输出作为上乘法器的载波输入。
因此,上乘法器的输出为
$$v_1\left ( t \right )=s\left ( t \right )c_1\left ( t \right )$$
将$s\left ( t \right )$和$c_1\left ( t \right )$的值代入上述方程。
$$\Rightarrow v_1\left ( t \right )=A_c \cos \left ( 2 \pi f_ct \right )m\left ( t \right ) \cos\left ( 2 \pi f_ct + \phi \right )$$
简化后,我们将得到$v_1\left ( t \right )$为
$$v_1\left ( t \right )=\frac{A_c}{2} \cos \phi m\left ( t \right )+\frac{A_c}{2} \cos\left ( 4 \pi f_ct + \phi \right )m\left ( t \right )$$
此信号作为上低通滤波器的输入。此低通滤波器的输出为
$$v_{01}\left ( t \right )=\frac{A_c}{2} \cos \phi m\left ( t \right )$$
因此,此低通滤波器的输出是调制信号的缩放版本。
$-90^0$移相器的输出为
$$c_2\left ( t \right )=cos\left ( 2 \pi f_ct + \phi-90^0 \right )= \sin\left ( 2 \pi f_ct + \phi \right )$$
此信号作为下乘法器的载波输入。
下乘法器的输出为
$$v_2\left ( t \right )=s\left ( t \right )c_2\left ( t \right )$$
将$s\left ( t \right )$和$c_2\left ( t \right )$的值代入上述方程。
$$\Rightarrow v_2\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )m\left ( t \right ) \sin \left ( 2 \pi f_ct + \phi \right )$$
简化后,我们将得到$v_2\left ( t \right )$为
$$v_2\left ( t \right )=\frac{A_c}{2} \sin \phi m\left ( t \right )+\frac{A_c}{2} \sin \left ( 4 \pi f_ct+ \phi \right )m\left ( t \right )$$
此信号作为下低通滤波器的输入。此低通滤波器的输出为
$$v_{02}\left ( t \right )=\frac{A_c}{2} \sin \phi m\left ( t \right )$$
此低通滤波器的输出与上低通滤波器的输出具有$-90^0$的相位差。
这两个低通滤波器的输出作为相位鉴别器的输入。根据这两个信号之间的相位差,相位鉴别器产生一个直流控制信号。
此信号作为VCO的输入,以校正VCO输出中的相位误差。因此,载波信号(用于DSBSC调制)和局部产生的信号(VCO输出)是同相的。