模拟通信 - DSBSC调制

---

---

在调幅过程中，调制波由载波和两个边带组成。调制波的信息只存在于边带中。边带只不过是一段包含功率的频率带，它们是载波频率的上下频率。

传输包含载波和两个边带的信号的过程，可以称为双边带全载波系统，简称为DSBFC。其波形图如下所示。

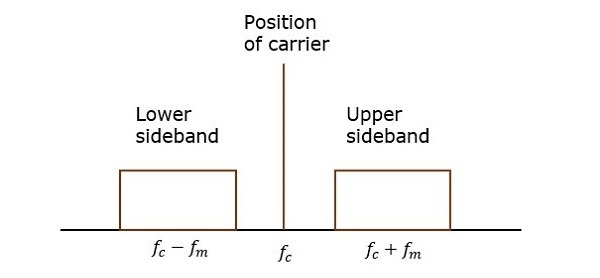
然而，这种传输效率低下。因为载波本身不携带信息，三分之二的功率被浪费在载波上。

如果抑制这个载波，并将节省的功率分配给两个边带，则此过程称为双边带抑制载波系统，简称为DSBSC。其波形图如下所示。

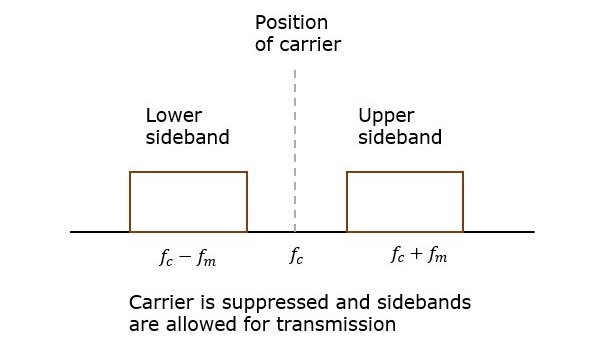
数学表达式

让我们考虑与前面章节中相同的调制信号和载波信号的数学表达式。

即，调制信号

$$m\left ( t \right )=A_m \cos \left ( 2 \pi f_mt\right )$$

载波信号

$$c\left ( t \right )=A_c \cos \left ( 2 \pi f_ct\right )$$

数学上，我们可以将DSBSC波的方程表示为调制信号和载波信号的乘积。

$$s\left ( t \right )=m\left ( t \right )c\left ( t \right )$$

$$\Rightarrow s\left ( t \right )=A_mA_c \cos \left ( 2 \pi f_mt \right )\cos \left ( 2 \pi f_ct \right )$$

DSBSC波的带宽

我们知道带宽(BW)的公式是

$$BW=f_{max}-f_{min}$$

考虑DSBSC调制波的方程。

$$s\left ( t \right )=A_mA_c \cos\left ( 2 \pi f_mt \right ) \cos(2 \pi f_ct)$$

$$\Rightarrow s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right ) t\right ]+\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c-f_m \right ) t\right ]$$

DSBSC调制波只有两个频率。因此，最大和最小频率分别为$f_c+f_m$和$f_c-f_m$。

即，

$f_{max}=f_c+f_m$ 和 $f_{min}=f_c-f_m$

将$f_{max}$和$f_{min}$的值代入带宽公式。

$$BW=f_c+f_m-\left ( f_c-f_m \right )$$

$$\Rightarrow BW=2f_m$$

因此，DSBSC波的带宽与AM波的带宽相同，等于调制信号频率的两倍。

DSBSC波的功率计算

考虑DSBSC调制波的以下方程。

$$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c+f_m \right ) t\right ]+\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c-f_m \right ) t\right ]$$

DSBSC波的功率等于上下边带频率分量的功率之和。

$$P_t=P_{USB}+P_{LSB}$$

我们知道余弦信号功率的标准公式是

$$P=\frac{{v_{rms}}^{2}}{R}=\frac{\left ( v_m\sqrt{2}\right )^2}{R}$$

首先，让我们分别求出上下边带的功率。

上边带功率

$$P_{USB}=\frac{\left ( A_mA_c / 2\sqrt{2}\right )^2}{R}=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$

同样，我们将得到下边带功率与上边带功率相同。

$$P_{LSB}=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$

现在，让我们将这两个边带功率相加，以得到DSBSC波的功率。

$$P_t=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}+\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$

$$\Rightarrow P_t=\frac{{A_{m}}^{2}{A_{c}}^{2}}{4R}$$

因此，传输DSBSC波所需的功率等于两个边带的功率之和。