
模拟通信 - DSBSC 调制器
在本章中,让我们讨论一下产生 DSBSC 波形的调制器。以下两种调制器可以产生 DSBSC 波形。
- 平衡调制器
- 环形调制器
平衡调制器
以下是平衡调制器的框图。
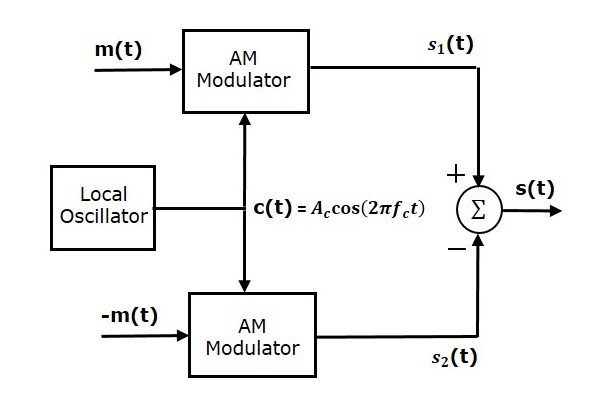
平衡调制器由两个相同的 AM 调制器组成。这两个调制器以平衡的配置排列,以抑制载波信号。因此,它被称为平衡调制器。
相同的载波信号 $c\left ( t \right )= A_c \cos \left ( 2 \pi f_ct \right )$ 作为输入信号之一应用于这两个 AM 调制器。调制信号 $m\left ( t \right )$ 作为另一个输入信号应用于上部 AM 调制器。而极性相反的调制信号 $m\left ( t \right )$,即 $-m\left ( t \right )$,则作为另一个输入信号应用于下部 AM 调制器。
上部 AM 调制器的输出为
$$s_1\left ( t \right )=A_c\left [1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
下部 AM 调制器的输出为
$$s_2\left ( t \right )=A_c\left [1-k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
我们通过从 $s_1\left ( t \right )$ 中减去 $s_2\left ( t \right )$ 来获得 DSBSC 波形 $s\left ( t \right )$。加法器块用于执行此操作。带有正号的 $s_1\left ( t \right )$ 和带有负号的 $s_2\left ( t \right )$ 作为输入信号应用于加法器块。因此,加法器块产生一个输出 $s\left ( t \right )$,它是 $s_1\left ( t \right )$ 和 $s_2\left ( t \right )$ 的差值。
$$\Rightarrow s\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )-A_c\left [ 1-k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
$$\Rightarrow s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )+A_ck_am\left ( t \right ) \cos\left ( 2 \pi f_ct \right )- A_c \cos\left ( 2 \pi f_ct \right )+$$
$A_ck_am\left ( t \right ) \cos\left ( 2 \pi f_ct \right )$
$\Rightarrow s\left ( t \right )=2A_ck_am\left ( t \right ) \cos\left ( 2 \pi f_ct \right )$
我们知道 DSBSC 波形的标准方程为
$$s\left ( t \right )=A_cm \left ( t \right ) \cos\left ( 2 \pi f_ct \right )$$
通过将加法器块的输出与 DSBSC 波形的标准方程进行比较,我们将得到比例因子为 $2k_a$。
环形调制器
以下是环形调制器的框图。
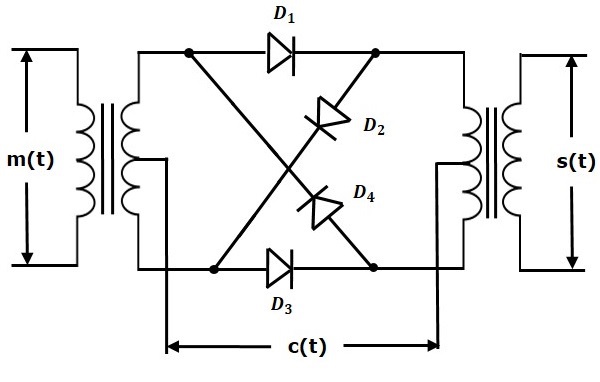
在此图中,四个二极管 $D_1$、$D_2$、$D_3$ 和 $D_4$ 以环形结构连接。因此,此调制器被称为环形调制器。在此图中使用了两个中心抽头的变压器。消息信号 $m\left ( t \right )$ 应用于输入变压器。而载波信号 $c\left ( t \right )$ 则应用于两个中心抽头的变压器之间。
对于载波信号的正半周期,二极管 $D_1$ 和 $D_3$ 导通,而另外两个二极管 $D_2$ 和 $D_4$ 则截止。在这种情况下,消息信号乘以 +1。
对于载波信号的负半周期,二极管 $D_2$ 和 $D_4$ 导通,而另外两个二极管 $D_1$ 和 $D_3$ 则截止。在这种情况下,消息信号乘以 -1。这会导致生成的 DSBSC 波形发生 $180^0$ 相移。
从以上分析可以看出,四个二极管 $D_1$、$D_2$、$D_3$ 和 $D_4$ 受载波信号控制。如果载波是方波,则 $c\left ( t \right )$ 的傅里叶级数表示为
$$c\left ( t \right )=\frac{4}{\pi}\sum_{n=1}^{\infty }\frac{\left ( -1 \right )^{n-1}}{2n-1} \cos\left [2 \pi f_ct\left ( 2n-1 \right ) \right ]$$
我们将得到 DSBSC 波形 $s\left ( t \right )$,它只是载波信号 $c\left ( t \right )$ 和消息信号 $m\left ( t \right )$ 的乘积,即
$$s\left ( t \right )=\frac{4}{\pi}\sum_{n=1}^{\infty }\frac{\left ( -1 \right )^{n-1}}{2n-1} \cos\left [2 \pi f_ct\left ( 2n-1 \right ) \right ]m\left ( t \right )$$
上述方程表示在环形调制器的输出变压器处获得的 DSBSC 波形。
DSBSC 调制器也称为乘积调制器,因为它们产生的输出是两个输入信号的乘积。