模拟通信 - 调频调制器

---

---

在本节中，让我们讨论一下产生窄带调频和宽带调频波的调制器。首先，让我们讨论窄带调频的产生。

窄带调频的产生

我们知道调频波的标准方程是

$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct+2 \pi k_f\int m\left ( t \right ) dt\right )$$

$\Rightarrow s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right ) \cos\left ( 2 \pi k_f\int m\left ( t \right )dt \right )-$

$A_c \sin\left ( 2 \pi f_ct \right ) \sin\left ( 2 \pi k_f\int m\left ( t \right )dt \right )$

对于窄带调频，

$$\left | 2 \pi k_f\int m\left ( t \right )dt \right | < < 1$$

我们知道当 $\theta$ 很小时，$\cos \theta \approx 1$ 且 $\sin \theta \approx 1$。

利用上述关系，我们将得到**窄带调频方程**为

$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )-A_c \sin\left ( 2 \pi f_ct \right )2 \pi k_f\int m\left ( t \right )dt$$

窄带调频调制器的框图如下所示。

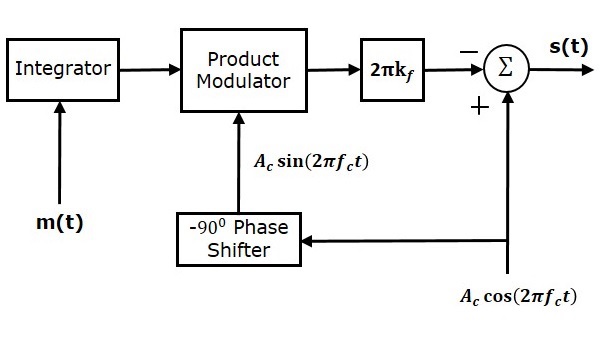
这里，积分器用于对调制信号 $m\left (t \right )$ 进行积分。载波信号 $A_c \cos \left ( 2 \pi f_ct \right )$ 通过 $-90^0$ 移相器进行 $-90^0$ 移相得到 $A_c \sin \left ( 2 \pi f_ct \right )$。乘法调制器有两个输入 $\int m\left ( t \right )dt$ 和 $A_c \sin \left ( 2 \pi f_ct \right )$。它产生一个输出，该输出是这两个输入的乘积。

通过在正向路径中放置一个 $2 \pi k_f$ 模块，将其进一步乘以 $2 \pi k_f$。加法器模块有两个输入，它们正是窄带调频方程的两个项。在加法器模块的输入端，为载波信号和其他项分配正负号。最后，加法器模块产生窄带调频波。

宽带调频的产生

以下两种方法可以产生宽带调频波。

• 直接法
• 间接法

直接法

这种方法被称为直接法，因为我们直接产生宽带调频波。在这种方法中，电压控制振荡器 (VCO) 用于产生宽带调频。VCO 产生一个输出信号，其频率与输入信号电压成正比。这类似于调频波的定义。宽带调频波产生的框图如下所示。

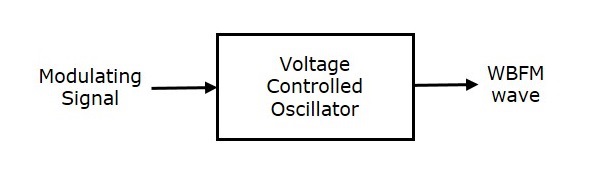
这里，调制信号 $m\left (t \right )$ 作为电压控制振荡器 (VCO) 的输入。VCO 产生一个输出，该输出正是宽带调频。

$$f_i \: \alpha \: m\left ( t \right )$$

$$\Rightarrow f_i=f_c+k_fm\left ( t \right )$$

其中，

$f_i$ 是宽带调频波的瞬时频率。

间接法

这种方法被称为间接法，因为我们间接产生宽带调频波。这意味着，我们首先产生窄带调频波，然后借助倍频器获得宽带调频波。宽带调频波产生的框图如下所示。

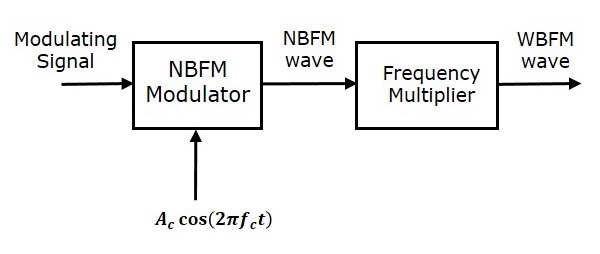
该框图主要包含两个阶段。在第一阶段，将使用窄带调频调制器产生窄带调频波。我们在本章开头已经看到了窄带调频调制器的框图。我们知道窄带调频波的调制指数小于 1。因此，为了获得调频波所需的调制指数（大于 1），请正确选择倍频器的值。

**倍频器**是一种非线性器件，它产生的输出信号的频率是输入信号频率的 'n' 倍。其中，'n' 是倍频因子。

如果将调制指数 $\beta$ 小于 1 的窄带调频波作为倍频器的输入，则倍频器会产生一个输出信号，其调制指数是 $\beta$ 的 'n' 倍，频率也是宽带调频波频率的 'n' 倍。

有时，我们可能需要多个阶段的倍频器和混频器才能增加调频波的频率偏移和调制指数。