
模拟通信 - 单边带抑制载波调制器
本章我们将讨论产生SSB(单边带抑制载波)波的调制器。我们可以使用以下两种方法产生SSB波。
- 频率鉴别法
- 相位鉴别法
频率鉴别法
下图显示了使用频率鉴别法的SSB调制器的框图。
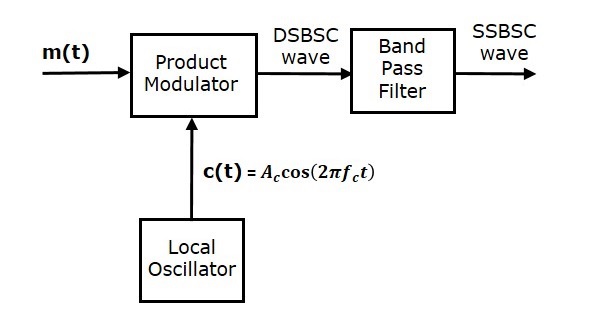
在这种方法中,我们首先使用乘法调制器产生DSB-SC(双边带抑制载波)波。然后,将此DSB-SC波作为带通滤波器的输入。该带通滤波器产生一个输出,即SSB波。
选择带通滤波器的频率范围作为所需SSB波的频谱。这意味着带通滤波器可以调谐到上边带或下边带频率,以获得具有上边带或下边带的相应SSB波。
相位鉴别法
下图显示了使用相位鉴别法的SSB调制器的框图。
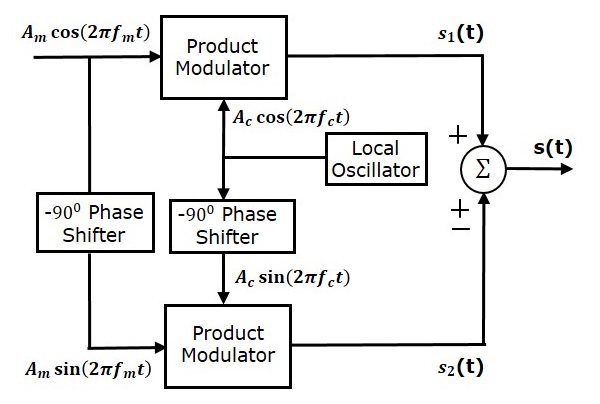
该框图由两个乘法调制器、两个-90°相移器、一个本地振荡器和一个求和器组成。乘法调制器产生一个输出,它是两个输入的乘积。-90°相移器产生一个输出,该输出相对于输入滞后-90°。
本地振荡器用于产生载波信号。求和器产生一个输出,该输出根据输入的极性,是两个输入的和或差。
调制信号$A_m \cos\left ( 2 \pi f_mt \right )$和载波信号$A_c \cos\left ( 2 \pi f_ct \right )$直接作为输入应用于上乘法调制器。因此,上乘法调制器产生一个输出,它是这两个输入的乘积。
上乘法调制器的输出为
$$s_1\left ( t \right )=A_mA_c \cos \left ( 2 \pi f_mt \right ) \cos\left ( 2 \pi f_ct \right )$$
$$ \Rightarrow s_1\left ( t \right )=\frac{A_mA_c}{2} \left \{ \cos \left [ 2 \pi\left ( f_c+f_m \right )t \right ]+ \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ] \right \}$$
调制信号$A_m \cos\left ( 2 \pi f_mt \right )$和载波信号$A_c \cos\left ( 2 \pi f_ct \right )$在作为下乘法调制器的输入之前,先进行-90°相移。因此,下乘法调制器产生一个输出,它是这两个输入的乘积。
下乘法调制器的输出为
$$s_2\left ( t \right )=A_mA_c \cos\left ( 2 \pi f_mt-90^0 \right ) \cos\left (2 \pi f_ct-90^0 \right )$$
$\Rightarrow s_2\left ( t \right )=A_mA_c \sin \left ( 2 \pi f_mt \right )\sin \left ( 2 \pi f_ct \right )$
$\Rightarrow s_2\left ( t \right )=\frac{A_mA_c}{2} \left \{ \cos \left [ 2 \pi\left ( f_c-f_m \right )t \right ]- \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \right \}$
将$s_1\left ( t \right )$和$s_2\left ( t \right )$相加,即可得到具有下边带的SSB调制波$s\left ( t \right )$。
$s\left ( t \right )=\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ]+\cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ] \right \}+$
$\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ]-\cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \right \}$
$\Rightarrow s\left ( t \right )=A_mA_c \cos \left [ 2 \pi\left ( f_c-f_m \right )t \right ]$
从$s_1\left ( t \right )$中减去$s_2\left ( t \right )$,即可得到具有上边带的SSB调制波$s\left ( t \right )$。
$s\left ( t \right )=\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ]+\cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ] \right \}-$
$\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ]-\cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \right \}$
$\Rightarrow s\left ( t \right )=A_mA_c \cos \left [ 2 \pi\left ( f_c+f_m \right )t \right ]$
因此,通过正确选择求和器输入的极性,我们将得到具有上边带或下边带的SSB波。