
模拟通信 - 残留边带抑制载波调制
在之前的章节中,我们讨论了SSBSC调制和解调。SSBSC调制信号只有一个边带频率。理论上,我们可以使用理想的带通滤波器完全获得一个边带频率分量。然而,实际上我们可能无法获得整个边带频率分量。由于这个原因,一些信息会丢失。
为了避免这种损失,选择了一种介于DSBSC和SSBSC之间的技术。这种技术被称为**残留边带抑制载波(VSBSC)**技术。“残留”一词意为“一部分”,名称由此而来。
**VSBSC调制**是一种过程,其中一部分信号(称为残留)与一个边带一起被调制。VSBSC波的频谱如下图所示。
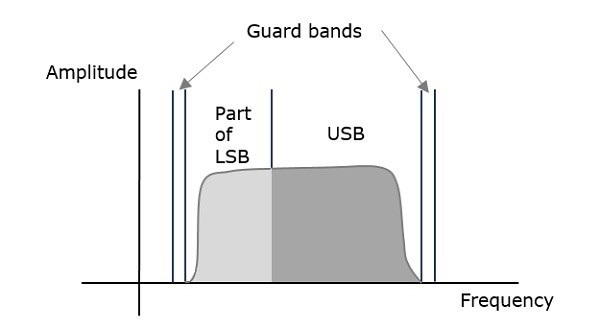
除了上边带,这种技术还会传输一部分下边带。类似地,我们可以传输下边带以及一部分上边带。为了避免干扰,在VSB的两侧都设置了一个非常小的保护带。VSB调制主要用于电视传输。
VSBSC调制的带宽
我们知道SSBSC调制波的带宽为$f_m$。由于VSBSC调制波包含一个边带的频率分量以及另一个边带的残留分量,因此其带宽将是SSBSC调制波带宽和残留频率$f_v$之和。
即,VSBSC调制波的带宽 = $f_m + f_v$
优点
以下是VSBSC调制的优点。
效率高。
与AM和DSBSC波相比,带宽减小。
滤波器设计简单,不需要高精度。
可以轻松传输低频分量。
具有良好的相位特性。
缺点
以下是VSBSC调制的缺点。
与SSBSC波相比,带宽更大。
解调复杂。
应用
VSBSC最突出和标准的应用是电视信号的传输。此外,在考虑带宽使用率时,这也是最方便和最有效率的技术。
现在,让我们分别讨论一下产生VSBSC波的调制器和解调VSBSC波的解调器。
VSBSC的产生
VSBSC波的产生类似于SSBSC波的产生。VSBSC调制器如下图所示。
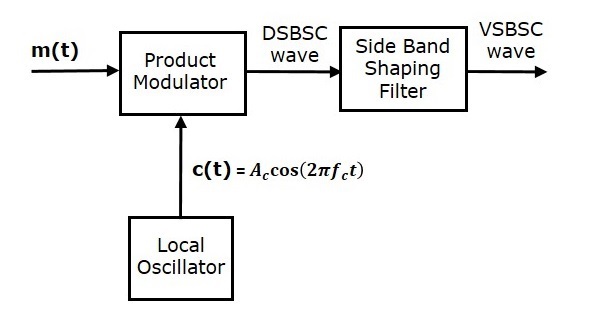
在这种方法中,我们首先将使用乘法调制器产生DSBSC波。然后,将此DSBSC波作为边带整形滤波器的输入。该滤波器产生一个输出,即VSBSC波。
调制信号$m\left ( t \right )$和载波信号$A_c \cos \left ( 2 \pi f_ct \right )$作为输入应用于乘法调制器。因此,乘法调制器产生的输出是这两个输入的乘积。
因此,乘法调制器的输出为
$$p\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )m\left ( t \right )$$
对两边应用傅里叶变换
$$P\left ( f \right )=\frac{A_c}{2}\left [ M\left ( f-f_c \right )+M\left ( f+f_c \right ) \right ]$$
上述方程表示DSBSC频谱方程。
设边带整形滤波器的传递函数为$H\left ( f \right )$。该滤波器的输入为$p\left ( t \right )$,输出为VSBSC调制波$s\left ( t \right )$。$p\left ( t \right )$和$s\left ( t \right )$的傅里叶变换分别为$P\left ( t \right )$和$S\left ( t \right )$。
数学上,我们可以将$S\left ( f \right )$写成
$$S\left ( t \right )=P\left ( f \right )H\left ( f \right )$$
将$P\left ( f \right )$的值代入上式。
$$S\left ( f \right )=\frac{A_c}{2}\left [ M\left ( f-f_c \right )+M\left ( f+f_c \right ) \right ]H\left ( f \right )$$
上述方程表示VSBSC频谱方程。
VSBSC的解调
VSBSC波的解调类似于SSBSC波的解调。这里,使用相同的载波信号(用于产生VSBSC波)来检测消息信号。因此,这个检测过程被称为**相干**或**同步检测**。VSBSC解调器如下图所示。
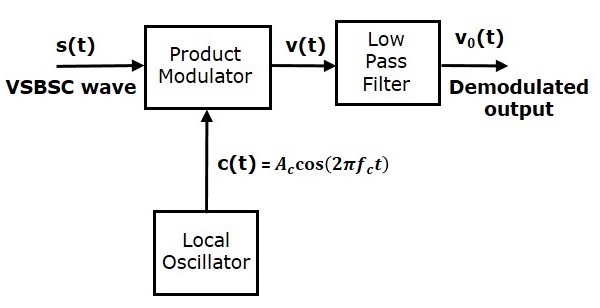
在这个过程中,可以通过将VSBSC波与具有与VSBSC调制中使用的载波相同频率和相位的载波相乘来提取消息信号。然后将所得信号通过低通滤波器。该滤波器的输出是所需的消息信号。
设VSBSC波为$s\left ( t \right )$,载波信号为$A_c \cos \left ( 2 \pi f_ct \right )。
从图中,我们可以将乘法调制器的输出写成
$$v\left ( t \right )= A_c \cos\left ( 2 \pi f_ct \right )s\left ( t \right )$$
对两边应用傅里叶变换
$$V\left ( f \right )= \frac{A_c}{2}\left [ S\left ( f-f_c \right )+S\left ( f+f_c \right ) \right ]$$
我们知道$S\left ( f \right )=\frac{A_c}{2}\left [ M\left ( f-f_c \right ) + M\left ( f+f_c \right )\right ]H\left ( f \right )$
从上式,让我们求出$S\left ( f-f_c \right )$和$S\left ( f+f_c \right )。
$$S\left ( f-f_c \right )=\frac{A_c}{2}\left [ M\left ( f-f_c-f_c \right ) + M\left ( f-f_c+f_c \right )\right ]H\left ( f-f_c \right )$$
$\Rightarrow S\left ( f-f_c \right )=\frac{A_c}{2}\left [ M\left ( f-2f_c \right )+M\left ( f \right ) \right ] H\left ( f-f_c \right )$
$$S\left ( f+f_c \right )=\frac{A_c}{2}\left [ M\left ( f+f_c-f_c \right ) +M\left ( f+f_c+f_c \right )\right ] H\left ( f+f_c \right )$$
$\Rightarrow S\left ( f+f_c \right )=\frac{A_c}{2}\left [ M \left ( f \right )+M \left (f+2f_c \right ) \right ] H \left ( f+f_c \right )$
将$S\left ( f-f_c \right )$和$S\left ( f+f_c \right )$的值代入$V\left ( f \right )。
$V(f) = \frac{A_c}{2}[\frac{A_c}{2}[M(f-2f_c)+M(f)]H(f-f_c)+$
$\frac{A_c}{2}[M(f)+M(f+2f_c)]H(f+f_c)]$
$\Rightarrow V\left ( f \right )=\frac{{A_{c}}^{2}}{4} M\left ( f \right )\left [ H\left ( f-f_c \right )+H \left ( f+f_c \right ) \right ]$
$+ \frac{{A_{c}}^{2}}{4}\left [ M\left ( f-2f_c \right )H\left ( f-f_c \right )+M\left ( f+2f_c \right )H\left ( f+f_c \right ) \right ]$
在上式中,第一项表示所需消息信号频谱的缩放版本。可以通过将上述信号通过低通滤波器来提取它。
$$V_0\left ( f \right )=\frac{{A_{c}}^{2}}{4} M\left ( f \right )\left [ H\left ( f-f_c \right )+H\left ( f+f_c \right ) \right ]$$