模拟通信 - 调频解调器

本章我们将讨论解调FM波的解调器。以下两种方法可以解调FM波。

• 频率鉴别法
• 相位鉴别法

频率鉴别法

我们知道FM波的方程为

$$s\left ( t \right ) =A_c \cos \left ( 2 \pi f_ct+2 \pi k_f \int m\left ( t \right )dt \right )$$

对上述方程关于't'求导。

$$\frac{ds\left ( t \right )}{dt}= -A_c\left ( 2 \pi f_c+2 \pi k_fm\left ( t \right ) \right ) \sin\left ( 2 \pi f_ct+2 \pi k_f\int m\left ( t \right )dt \right )$$

我们可以将$-\sin \theta$ 写作 $\sin \left ( \theta -180^0 \right )$.

$$\Rightarrow \frac{ds(t)}{dt}=A_c\left ( 2 \pi f_c+2 \pi k_fm\left ( t \right ) \right )\sin\left ( 2 \pi f_ct+2 \pi k_f \int m\left ( t \right )dt-180^0 \right )$$

$$\Rightarrow \frac{ds(t)}{dt}=A_c\left ( 2 \pi f_c \right )\left [ 1+\left ( \frac{k_f}{k_c} \right )m\left ( t \right ) \right ] \sin\left ( 2 \pi f_ct+2 \pi k_f\int m\left ( t \right )dt-180^0 \right )$$

在上述方程中，幅度项类似于AM波的包络，角度项类似于FM波的角度。这里，我们需要的是调制信号$m\left ( t \right )$。因此，我们可以从AM波的包络中恢复它。

下图显示了使用频率鉴别法的FM解调器的框图。

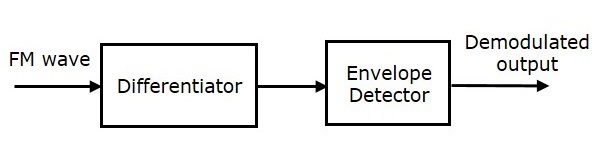
该框图由微分器和包络检波器组成。微分器用于将FM波转换为AM波和FM波的组合。这意味着它将FM波的频率变化转换为AM波相应的电压（幅度）变化。我们知道包络检波器的操作。它产生AM波的解调输出，这也就是调制信号。

相位鉴别法

下图显示了使用相位鉴别法的FM解调器的框图。

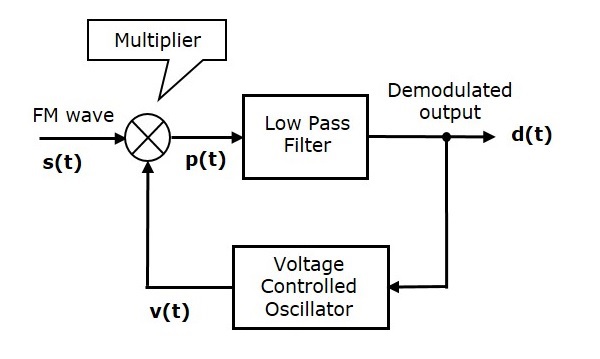
该框图由乘法器、低通滤波器和压控振荡器(VCO)组成。VCO产生一个输出信号$v \left ( t \right )$，其频率与输入信号电压$d \left ( t \right )$成比例。最初，当信号$d \left ( t \right )$为零时，调整VCO以产生输出信号$v \left ( t \right )$，其具有载波频率，并且相对于载波信号具有$-90^0$的相移。

将FM波$s \left ( t \right )$和VCO输出$v \left ( t \right )$作为乘法器的输入。乘法器产生一个输出，该输出具有高频分量和低频分量。低通滤波器消除高频分量，只产生低频分量作为其输出。

这个低频分量只包含与相位差相关的项。因此，我们从低通滤波器的这个输出得到调制信号$m \left ( t \right )$。