
单边带抑制载波解调器
从SSBSC波中提取原始消息信号的过程称为SSBSC的检测或解调。相干检测器用于解调SSBSC波。
相干检测器
在这里,相同的载波信号(用于生成SSBSC波)用于检测消息信号。因此,此检测过程称为**相干**或**同步检测**。以下是相干检测器的框图。
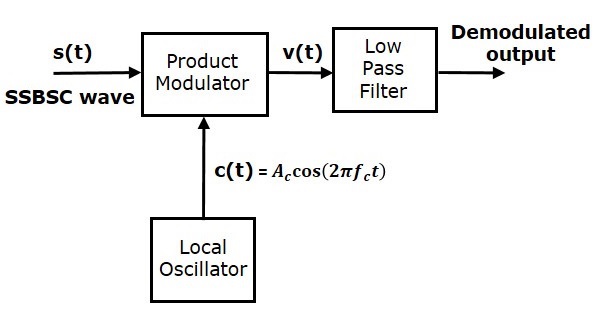
在此过程中,可以通过将消息信号与具有与SSBSC调制中使用的载波相同频率和相位的载波相乘来从SSBSC波中提取消息信号。然后将得到的信号通过低通滤波器。该滤波器的输出是所需的消息信号。
考虑以下具有**下边带**的SSBSC波。
$$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ]$$
本地振荡器的输出为
$$c\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )$$
从图中,我们可以将乘积调制器的输出写成
$$v\left ( t \right )=s\left ( t \right )c\left ( t \right )$$
将$s\left ( t \right )$和$c\left ( t \right )$的值代入上述方程。
$$v\left ( t \right )=\frac{A_mA_c}{2} \cos \left [ 2 \pi \left ( f_c-f_m \right )t \right ] A_c \cos \left ( 2 \pi f_ct \right )$$
$=\frac{A_m{A_{c}}^{2}}{2} \cos\left [ 2 \pi\left ( f_c -f_m \right )t \right ] \cos\left ( 2 \pi f_ct \right )$
$=\frac{A_m{A_{c}}^{2}}{4}\left \{ \cos\left [ 2 \pi\left ( 2f_c-fm \right ) \right ]+ \cos\left ( 2 \pi f_m \right )t \right \}$
$v\left ( t \right )=\frac{A_m{A_{c}}^{2}}{4} \cos\left ( 2 \pi f_mt \right )+\frac{A_m{A_{c}}^{2}}{4} \cos\left [ 2 \pi \left ( 2f_c-f_m \right )t \right ]$
在上式中,第一项是消息信号的缩放版本。可以通过将上述信号通过低通滤波器来提取它。
因此,低通滤波器的输出为
$$v_0\left ( t \right )=\frac{A_m{A_{c}}^{2}}{4} \cos\left ( 2 \pi f_mt \right )$$
这里,缩放因子为$\frac{{A_{c}}^{2}}{4}$。
我们可以使用相同的框图来解调具有上边带的SSBSC波。考虑以下具有**上边带**的SSBSC波。
$$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c+f_m \right )t \right ]$$
本地振荡器的输出为
$$c\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )$$
我们可以将乘积调制器的输出写成
$$v\left ( t \right )=s\left ( t \right )c\left ( t \right )$$
将$s\left ( t \right )$和$c\left ( t \right )$的值代入上述方程。
$$\Rightarrow v\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ]A_c \cos\left ( 2 \pi f_ct \right )$$
$=\frac{A_m{A_{c}}^{2}}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \cos\left ( 2 \pi f_ct \right )$
$=\frac{A_m{A_{c}}^{2}}{4} \left \{ \cos\left [ 2 \pi\left ( 2f_c+f_m \right )t \right ]+ \cos\left ( 2 \pi f_mt \right ) \right \}$
$v\left ( t \right )=\frac{A_m{A_{c}}^{2}}{4} \cos\left ( 2 \pi f_mt \right )+\frac{A_m{A_{c}}^{2}}{4} \cos \left [ 2 \pi\left ( 2f_c+f_m \right )t \right ]$
在上式中,第一项是消息信号的缩放版本。可以通过将上述信号通过低通滤波器来提取它。
因此,低通滤波器的输出为
$$v_0\left ( t \right )=\frac{A_m{A_{c}}^{2}}{4} \cos\left ( 2 \pi f_mt \right )$$
这里,缩放因子也是$\frac{{A_{c}}^{2}}{4}$。
因此,在两种情况下,使用相干检测器都可以得到相同的解调输出。