灰度级分辨率

---

---

图像分辨率

分辨率可以定义为图像中像素的总数。这在图像分辨率中已经讨论过。我们还讨论过，图像的清晰度并不取决于像素的数量，而是取决于图像的空间分辨率。这在空间分辨率中已经讨论过。在这里，我们将讨论另一种类型的分辨率，称为灰度级分辨率。

灰度级分辨率

灰度级分辨率是指图像中阴影或灰度水平的可预测或确定性变化。

简而言之，灰度级分辨率等于每像素的比特数。

我们已经在每像素比特数和图像存储需求的教程中讨论了每像素比特数。我们将在本文中简要定义 bpp。

BPP

图像中不同颜色的数量取决于颜色深度或每像素的比特数。

数学上

可以在灰度级分辨率和每像素比特数之间建立的数学关系可以表示为。

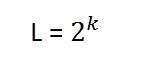
在这个等式中，L 指的是灰度级的数量。它也可以定义为灰度的阴影。而 k 指的是 bpp 或每像素的比特数。因此，2 的每像素比特数次幂等于灰度级分辨率。

例如

上面爱因斯坦的图像是灰度图像。意味着它是一张每像素 8 位或 8bpp 的图像。

现在如果要计算灰度级分辨率，我们将这样操作。

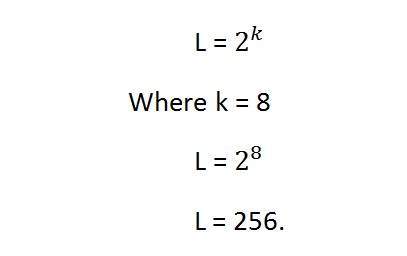
这意味着它的灰度级分辨率为 256。或者换句话说，这张图像有 256 种不同的灰度阴影。

图像的每像素比特数越高，其灰度级分辨率越高。

根据 BPP 定义灰度级分辨率

灰度级分辨率不一定要仅根据级别来定义。我们也可以根据每像素的比特数来定义它。

示例

如果您得到一张 4 bpp 的图像，并被要求计算其灰度级分辨率。这个问题有两个答案。

第一个答案是 16 个级别。

第二个答案是 4 位。

从灰度级分辨率中查找 bpp

您还可以从给定的灰度级分辨率中找到每像素的比特数。为此，我们只需要稍微修改一下公式。

公式 1。

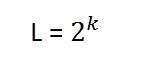
此公式查找级别。现在如果我们要查找每像素的比特数，在本例中为 k，我们将简单地将其更改为如下所示。

K = log 以 2 为底 (L) 公式 (2)

因为在第一个公式中，级别 (L) 和每像素比特数 (k) 之间的关系是指数关系。现在我们必须将其反转，因此指数的反函数是 log。

让我们举一个例子，从灰度级分辨率中查找每像素的比特数。

例如

如果您得到一张 256 个级别的图像。它需要多少每像素的比特数。

将 256 代入公式，我们得到。

K = log 以 2 为底 (256)

K = 8。

所以答案是每像素 8 位。

灰度级分辨率和量化

量化将在下一个教程中正式介绍，但在这里我们只是要解释灰度级分辨率和量化之间的关系。

灰度级分辨率在信号的 y 轴上找到。在信号与系统导论教程中，我们学习过对模拟信号进行数字化需要两个步骤。采样和量化。

采样在 x 轴上进行。量化在 Y 轴上进行。

因此，这意味着图像的灰度级分辨率的数字化是在量化中完成的。