透视变换

---

---

当人眼看近处物体时，相比远处物体看起来更大。这通常被称为透视。而变换是指物体等从一种状态转换到另一种状态。

总的来说，透视变换处理的是将三维世界转换为二维图像的过程。这与人眼的视觉原理相同，也与相机的工作原理相同。

我们将详细探讨为什么近处的物体看起来更大，而远处的物体看起来更小，即使当你靠近它们时，它们看起来会更大。

我们将从参考系的概念开始讨论。

参考系

参考系基本上是一组参考值，我们根据这些值来测量某事物。

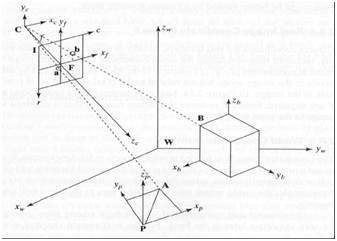
五个参考系

为了分析三维世界/图像/场景，需要五个不同的参考系。

• 物体
• 世界
• 相机
• 图像
• 像素

1. 物体坐标系

物体坐标系用于对物体建模。例如，检查特定物体相对于其他物体是否处于正确位置。它是一个三维坐标系。

2. 世界坐标系

世界坐标系用于关联三维世界中的物体。它是一个三维坐标系。

3. 相机坐标系

相机坐标系用于关联相对于相机的物体。它是一个三维坐标系。

4. 图像坐标系

它不是三维坐标系，而是一个二维系统。它用于描述如何将三维点映射到二维图像平面。

5. 像素坐标系

它也是一个二维坐标系。每个像素都有一个像素坐标值。

这五个参考系之间的变换

这就是三维场景如何转换为具有像素图像的二维图像。

现在我们将用数学方法解释这个概念。

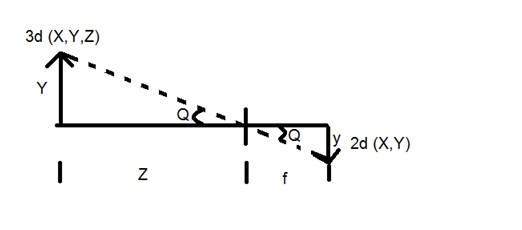
其中

Y = 三维物体

y = 二维图像

f = 相机的焦距

Z = 物体与相机之间的距离

现在，在这个变换中形成了两个不同的角度，用Q表示。

第一个角度是

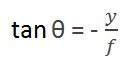
其中负号表示图像倒置。形成的第二个角度是

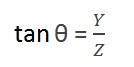
比较这两个方程，我们得到

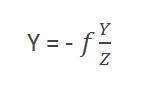
从这个方程可以看出，当光线从物体反射后经过相机时，会形成一个倒立的图像。

我们可以通过这个例子更好地理解这一点。

例如

计算所成图像的大小

假设拍摄了一个身高5米的人的图像，此人距离相机50米，我们必须说明，如果相机的焦距为50毫米，则该人的图像大小是多少。

解答

由于焦距以毫米为单位，因此为了计算，我们必须将所有内容都转换为毫米。

所以，

Y = 5000 毫米。

f = 50 毫米。

Z = 50000 毫米。

将这些值代入公式，我们得到

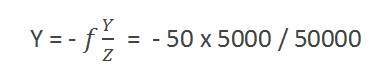
= -5 毫米。

再次，负号表示图像倒置。