卷积与相关

卷积

卷积是一种数学运算，用于表达线性时不变 (LTI) 系统的输入和输出之间的关系。它将 LTI 系统的输入、输出和冲激响应关联起来，如下所示：

$$ y (t) = x(t) * h(t) $$

其中 y (t) = LTI 的输出

x (t) = LTI 的输入

h (t) = LTI 的冲激响应

卷积有两种类型：

连续卷积
离散卷积

连续卷积

$ y(t) \,\,= x (t) * h (t) $

$= \int_{-\infty}^{\infty} x(\tau) h (t-\tau)d\tau$

(或)

$= \int_{-\infty}^{\infty} x(t - \tau) h (\tau)d\tau $

离散卷积

$y(n)\,\,= x (n) * h (n)$

$= \Sigma_{k = - \infty}^{\infty} x(k) h (n-k) $

(或)

$= \Sigma_{k = - \infty}^{\infty} x(n-k) h (k) $

通过使用卷积，我们可以找到系统的零状态响应。

反卷积

反卷积是卷积的逆过程，广泛应用于信号和图像处理。

卷积的性质

交换律

$ x_1 (t) * x_2 (t) = x_2 (t) * x_1 (t) $

分配律

$ x_1 (t) * [x_2 (t) + x_3 (t) ] = [x_1 (t) * x_2 (t)] + [x_1 (t) * x_3 (t)]$

结合律

$x_1 (t) * [x_2 (t) * x_3 (t) ] = [x_1 (t) * x_2 (t)] * x_3 (t) $

移位性质

$ x_1 (t) * x_2 (t) = y (t) $

$ x_1 (t) * x_2 (t-t_0) = y (t-t_0) $

$ x_1 (t-t_0) * x_2 (t) = y (t-t_0) $

$ x_1 (t-t_0) * x_2 (t-t_1) = y (t-t_0-t_1) $

与冲激的卷积

$ x_1 (t) * \delta (t) = x(t) $

$ x_1 (t) * \delta (t- t_0) = x(t-t_0) $

单位阶跃函数的卷积

$ u (t) * u (t) = r(t) $

$ u (t-T_1) * u (t-T_2) = r(t-T_1-T_2) $

$ u (n) * u (n) = [n+1] u(n) $

缩放性质

如果 $x (t) * h (t) = y (t) $

则 $x (a t) * h (a t) = {1 \over |a|} y (a t)$

输出的微分

如果 $y (t) = x (t) * h (t)$

则 $ {dy (t) \over dt} = {dx(t) \over dt} * h (t) $

或

$ {dy (t) \over dt} = x (t) * {dh(t) \over dt}$

注意

两个因果序列的卷积是因果的。
两个反因果序列的卷积是反因果的。
两个不等长矩形的卷积结果为梯形。
两个等长矩形的卷积结果为三角形。
一个函数与其自身的卷积等于该函数的积分。

示例：您知道 $u(t) * u(t) = r(t)$

根据以上说明，$u(t) * u(t) = \int u(t)dt = \int 1dt = t = r(t)$

在这里，您只需对 $u(t)$ 进行积分即可得到结果。

卷积信号的范围

如果两个信号进行卷积，则得到的卷积信号具有以下范围：

下限之和 < t < 上限之和

例如：求下面给出的信号卷积的范围

这里，我们有两个不等长的矩形进行卷积，结果为梯形。

卷积信号的范围是

下限之和 < t < 上限之和

$-1+-2 < t < 2+2 $

$-3 < t < 4 $

因此，结果是周期为 7 的梯形。

卷积信号的面积

卷积信号下的面积由 $A_y = A_x A_h$ 给出

其中 A_x = 输入信号下的面积

A_h = 冲激响应下的面积

A_y = 输出信号下的面积

证明： $y(t) = \int_{-\infty}^{\infty} x(\tau) h (t-\tau)d\tau$

两边取积分

$ \int y(t)dt \,\,\, =\int \int_{-\infty}^{\infty}\, x (\tau) h (t-\tau)d\tau dt $

$ =\int x (\tau) d\tau \int_{-\infty}^{\infty}\, h (t-\tau) dt $

我们知道任何信号的面积就是该信号本身的积分。

$\therefore A_y = A_x\,A_h$

直流分量

任何信号的直流分量由下式给出：

$\text{直流分量}={\text{信号的面积} \over \text{信号的周期}}$

例如：下面给出的卷积信号的直流分量是多少？

dc component of the resultant convoluted signal

这里 x₁(t) 的面积 = 长度 × 宽度 = 1 × 3 = 3

x₂(t) 的面积 = 长度 × 宽度 = 1 × 4 = 4

卷积信号的面积 = x₁(t) 的面积 × x₂(t) 的面积

= 3 × 4 = 12

卷积信号的持续时间 = 下限之和 < t < 上限之和

= -1 + -2 < t < 2+2

= -3 < t < 4

周期=7

$\therefore$ 卷积信号的直流分量 = $\text{信号的面积} \over \text{信号的周期}$

直流分量 = ${12 \over 7}$

离散卷积

让我们看看如何计算离散卷积

i. 计算离散线性卷积

对两个序列 x[n] = {a,b,c} 和 h[n] = [e,f,g] 进行卷积

卷积输出 = [ ea, eb+fa, ec+fb+ga, fc+gb, gc]

注意：如果两个序列分别有 m、n 个样本，则得到的卷积序列将有 [m+n-1] 个样本。

示例：对两个序列 x[n] = {1,2,3} 和 h[n] = {-1,2,2} 进行卷积

卷积输出 y[n] = [ -1, -2+2, -3+4+2, 6+4, 6]

= [-1, 0, 3, 10, 6]

这里 x[n] 包含 3 个样本，h[n] 也包含 3 个样本，因此得到的序列有 3+3-1 = 5 个样本。

ii. 计算周期性或循环卷积

周期性卷积对离散傅里叶变换有效。要计算周期性卷积，所有样本必须是实数。周期性或循环卷积也称为快速卷积。

如果分别长度为 m、n 的两个序列使用循环卷积进行卷积，则得到的序列将具有 max [m,n] 个样本。

例如：使用循环卷积对两个序列 x[n] = {1,2,3} 和 h[n] = {-1,2,2} 进行卷积

正常的卷积输出 y[n] = [ -1, -2+2, -3+4+2, 6+4, 6]。

= [-1, 0, 3, 10, 6]

这里 x[n] 包含 3 个样本，h[n] 也包含 3 个样本。因此，通过循环卷积得到的序列必须具有 max[3,3]= 3 个样本。

现在要获得周期性卷积结果，正常卷积的前 3 个样本（因为周期为 3）相同，接下来的两个样本添加到第一个样本中，如下所示

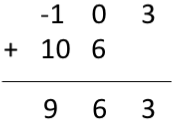
$\therefore$ 循环卷积结果 $y[n] = [9\quad 6\quad 3 ]$

自相关函数

它定义为信号与其自身的相关性。自相关函数是衡量信号与其延迟版本之间相似度的一种方法。它用 R($\tau$) 表示。

考虑一个信号 x(t)。x(t) 与其延迟版本的自相关函数由下式给出：

$$ R_{11} (\tau) = R (\tau) = \int_{-\infty}^{\infty} x(t)x(t-\tau) dt \quad \quad \text{[+ve shift]} $$

$$\quad \quad \quad \quad \quad = \int_{-\infty}^{\infty} x(t)x(t + \tau) dt \quad \quad \text{[-ve shift]} $$

其中 $\tau$ = 搜索或扫描或延迟参数。

如果信号是复数，则自相关函数由下式给出：

$$ R_{11} (\tau) = R (\tau) = \int_{-\infty}^{\infty} x(t)x * (t-\tau) dt \quad \quad \text{[+ve shift]} $$

$$\quad \quad \quad \quad \quad = \int_{-\infty}^{\infty} x(t + \tau)x * (t) dt \quad \quad \text{[-ve shift]} $$

能量信号的自相关函数的性质

自相关表现出共轭对称性，即 R ($\tau$) = R*(-$\tau$)
能量信号在原点（即 $\tau$=0 处）的自相关函数等于该信号的总能量，表示为：

R (0) = E = $ \int_{-\infty}^{\infty}\,|\,x(t)\,|^2\,dt $
自相关函数 $\infty {1 \over \tau} $，
自相关函数在 $\tau$=0 处最大，即 |R ($\tau$) | ≤ R (0) ∀ $\tau$
自相关函数和能量谱密度是傅里叶变换对。即

$F.T\,[ R (\tau) ] = \Psi(\omega)$

$\Psi(\omega) = \int_{-\infty}^{\infty} R (\tau) e^{-j\omega \tau} d \tau$
$ R (\tau) = x (\tau)* x(-\tau) $

功率信号的自相关函数

周期为 T 的周期性功率信号的自相关函数由下式给出：

$$ R (\tau) = \lim_{T \to \infty} {1\over T} \int_{{-T \over 2}}^{{T \over 2}}\, x(t) x* (t-\tau) dt $$

性质

功率信号的自相关表现出共轭对称性，即 $ R (\tau) = R*(-\tau)$
功率信号在 $\tau = 0$（在原点）处自相关函数等于该信号的总功率。即

$R (0)= \rho $
功率信号的自相关函数 $\infty {1 \over \tau}$，
功率信号的自相关函数在 $\tau$ = 0 处最大，即

$ | R (\tau) | \leq R (0)\, \forall \,\tau$
自相关函数和功率谱密度是傅里叶变换对。即

$F.T[ R (\tau) ] = s(\omega)$

$s(\omega) = \int_{-\infty}^{\infty} R (\tau) e^{-j\omega \tau} d\tau$
$R (\tau) = x (\tau)* x(-\tau) $

密度谱

让我们看看密度谱

能量密度谱

能量密度谱可以使用以下公式计算：

$$ E = \int_{-\infty}^{\infty} |\,x(f)\,|^2 df $$

功率密度谱

功率密度谱可以使用以下公式计算：

$$P = \Sigma_{n = -\infty}^{\infty}\, |\,C_n |^2 $$

互相关函数

互相关是衡量两个不同信号之间相似度的一种方法。

考虑两个信号 x₁(t) 和 x₂(t)。这两个信号的互相关 $R_{12}(\tau)$ 由下式给出：

$$R_{12} (\tau) = \int_{-\infty}^{\infty} x_1 (t)x_2 (t-\tau)\, dt \quad \quad \text{[+ve shift]} $$

$$\quad \quad = \int_{-\infty}^{\infty} x_1 (t+\tau)x_2 (t)\, dt \quad \quad \text{[-ve shift]}$$

如果信号是复数，则

$$R_{12} (\tau) = \int_{-\infty}^{\infty} x_1 (t)x_2^{*}(t-\tau)\, dt \quad \quad \text{[+ve shift]} $$

$$\quad \quad = \int_{-\infty}^{\infty} x_1 (t+\tau)x_2^{*} (t)\, dt \quad \quad \text{[-ve shift]}$$

$$R_{21} (\tau) = \int_{-\infty}^{\infty} x_2 (t)x_1^{*}(t-\tau)\, dt \quad \quad \text{[+ve shift]} $$

$$\quad \quad = \int_{-\infty}^{\infty} x_2 (t+\tau)x_1^{*} (t)\, dt \quad \quad \text{[-ve shift]}$$

能量和功率信号的互相关函数的性质

自相关表现出共轭对称性，即 $R_{12} (\tau) = R^*_{21} (-\tau)$。
互相关不像卷积那样满足交换律，即

$$ R_{12} (\tau) \neq R_{21} (-\tau) $$
如果 R₁₂(0) = 0，这意味着如果 $ \int_{-\infty}^{\infty} x_1 (t) x_2^* (t) dt = 0$，则这两个信号被称为正交的。

对于功率信号，如果 $ \lim_{T \to \infty} {1\over T} \int_{{-T \over 2}}^{{T \over 2}}\, x(t) x^* (t)\,dt $，则这两个信号被称为正交的。
互相关函数对应于一个信号的频谱与另一个信号的频谱的复共轭的乘积。即

$$ R_{12} (\tau) \leftarrow \rightarrow X_1(\omega) X_2^*(\omega)$$

这也被称为相关定理。

帕塞瓦尔定理

帕塞瓦尔定理对于能量信号指出，信号的总能量可以通过信号的频谱获得，如下所示：

$ E = {1\over 2 \pi} \int_{-\infty}^{\infty} |X(\omega)|^2 d\omega $

注意：如果一个信号的能量为E，那么该信号的时间尺度版本x(at)的能量为E/a。

打印页面