信号采样技术

---

---

有三种类型的采样技术

• 脉冲采样。

• 自然采样。

• 平顶采样。

脉冲采样

脉冲采样可以通过将输入信号 x(t) 与周期为 'T' 的脉冲序列 $\Sigma_{n=-\infty}^{\infty}\delta(t-nT)$ 相乘来实现。这里，脉冲的幅度随输入信号 x(t) 的幅度变化。采样器的输出由下式给出

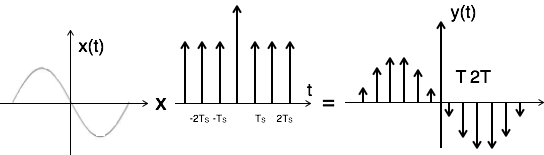
$y(t) = x(t) ×$ 脉冲序列

$= x(t) × \Sigma_{n=-\infty}^{\infty} \delta(t-nT)$

$ y(t) = y_{\delta} (t) = \Sigma_{n=-\infty}^{\infty}x(nt) \delta(t-nT)\,...\,... 1 $

为了得到采样信号的频谱，考虑对等式 1 两边进行傅里叶变换

$Y(\omega) = {1 \over T} \Sigma_{n=-\infty}^{\infty} X(\omega - n \omega_s ) $

这称为理想采样或脉冲采样。在实践中你无法使用它，因为脉冲宽度不可能为零，并且在实践中不可能产生脉冲序列。

自然采样

自然采样类似于脉冲采样，只是脉冲序列被周期为 T 的脉冲序列所取代。即你将输入信号 x(t) 乘以脉冲序列 $\Sigma_{n=-\infty}^{\infty} P(t-nT)$，如下所示

采样器的输出为

$y(t) = x(t) \times \text{脉冲序列}$

$= x(t) \times p(t) $

$= x(t) \times \Sigma_{n=-\infty}^{\infty} P(t-nT)\,...\,...(1) $

p(t) 的指数傅里叶级数表示可以表示为

$p(t) = \Sigma_{n=-\infty}^{\infty} F_n e^{j n\omega_s t}\,...\,...(2) $

$= \Sigma_{n=-\infty}^{\infty} F_n e^{j 2 \pi nf_s t} $

其中 $F_n= {1 \over T} \int_{-T \over 2}^{T \over 2} p(t) e^{-j n \omega_s t} dt$

$= {1 \over TP}(n \omega_s)$

将 F_n 值代入等式 2

$ \therefore p(t) = \Sigma_{n=-\infty}^{\infty} {1 \over T} P(n \omega_s)e^{j n \omega_s t}$

$ = {1 \over T} \Sigma_{n=-\infty}^{\infty} P(n \omega_s)e^{j n \omega_s t}$

将 p(t) 代入等式 1

$y(t) = x(t) \times p(t)$

$= x(t) \times {1 \over T} \Sigma_{n=-\infty}^{\infty} P(n \omega_s)\,e^{j n \omega_s t} $

$y(t) = {1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\, x(t)\, e^{j n \omega_s t} $

为了得到采样信号的频谱，考虑对两边进行傅里叶变换。

$F.T\, [ y(t)] = F.T [{1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\, x(t)\, e^{j n \omega_s t}]$

$ = {1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\,F.T\,[ x(t)\, e^{j n \omega_s t} ] $

根据频移特性

$F.T\,[ x(t)\, e^{j n \omega_s t} ] = X[\omega-n\omega_s] $

$ \therefore\, Y[\omega] = {1 \over T} \Sigma_{n=-\infty}^{\infty} P( n \omega_s)\,X[\omega-n\omega_s] $

平顶采样

在传输过程中，在传输脉冲的顶部会引入噪声，如果脉冲呈平顶状，则可以很容易地去除这些噪声。这里，样本的顶部是平坦的，即它们具有恒定的幅度。因此，它被称为平顶采样或实际采样。平顶采样利用了采样保持电路。

理论上，采样信号可以通过矩形脉冲 p(t) 与理想采样信号（例如 y_δ(t)）进行卷积来获得，如图所示

即 $ y(t) = p(t) \times y_\delta (t)\, ... \, ...(1) $

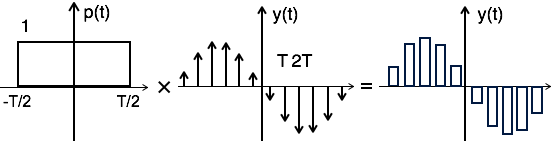
为了得到采样频谱，考虑对等式 1 两边进行傅里叶变换

$Y[\omega] = F.T\,[P(t) \times y_\delta (t)] $

根据卷积特性，

$Y[\omega] = P(\omega)\, Y_\delta (\omega)$

这里 $P(\omega) = T Sa({\omega T \over 2}) = 2 \sin \omega T/ \omega$

奈奎斯特率

它是信号可以转换为样本并可以无失真恢复的最小采样率。

奈奎斯特率 f_N = 2f_m hz

奈奎斯特间隔 = ${1 \over fN}$ = $ {1 \over 2fm}$ 秒。

带通信号的采样

对于带通信号，带通信号 X[ω] 的频谱在 f₁ ≤ f ≤ f₂ 范围之外的频率为 0。频率 f₁ 始终大于零。此外，当 f_s > 2f₂ 时没有混叠效应。但它有两个缺点

• 采样率与 f₂ 成正比。这在实践中存在局限性。

• 采样信号频谱存在频谱间隙。

为了克服这一点，带通定理指出，当采样频率 f_s < 2f₂ 时，输入信号 x(t) 可以转换为其样本并可以无失真恢复。

此外，

$$ f_s = {1 \over T} = {2f_2 \over m} $$

其中 m 是小于 ${f_2 \over B}$ 的最大整数

且 B 为信号的带宽。如果 f₂=KB，则

$$ f_s = {1 \over T} = {2KB \over m} $$

对于带宽为 2f_m 的带通信号，最小采样率 f_s= 2 B = 4f_m，

采样信号的频谱由 $Y[\omega] = {1 \over T} \Sigma_{n=-\infty}^{\infty}\,X[ \omega - 2nB]$ 给出