信号基本类型

---

---

以下是一些基本的信号

单位阶跃函数

单位阶跃函数用u(t)表示，定义为u(t) = $\left\{\begin{matrix}1 & t \geqslant 0\\ 0 & t<0 \end{matrix}\right.$

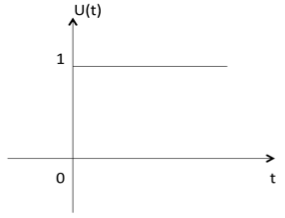
• 它被用作最佳测试信号。
• 单位阶跃函数下的面积为1。

单位冲激函数

冲激函数用δ(t)表示，定义为δ(t) = $\left\{\begin{matrix}1 & t = 0\\ 0 & t\neq 0 \end{matrix}\right.$

$$\int_{-\infty}^{\infty} δ(t)dt=u (t)$$

$$\delta(t) = {du(t) \over dt }$$

斜坡信号

斜坡信号用r(t)表示，定义为r(t) = $\left\{\begin {matrix}t & t\geqslant 0\\ 0 & t < 0 \end{matrix}\right.$

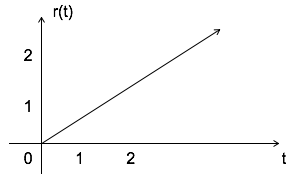
$$\int u(t) = \int 1 = t = r(t)$$

$$u(t) = {dr(t) \over dt}$$

单位斜坡下的面积为1。

抛物线信号

抛物线信号可以定义为x(t) = $\left\{\begin{matrix} t^2/2 & t \geqslant 0\\ 0 & t < 0 \end{matrix}\right.$

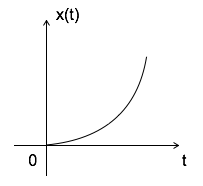
$$\iint u(t)dt = \int r(t)dt = \int t dt = {t^2 \over 2} = 抛物线信号$$

$$\Rightarrow u(t) = {d^2x(t) \over dt^2}$$

$$\Rightarrow r(t) = {dx(t) \over dt}$$

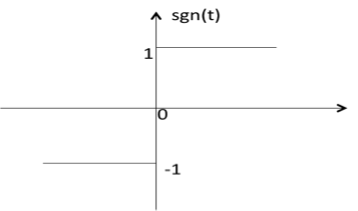
符号函数

符号函数用sgn(t)表示，定义为sgn(t) = $\left\{\begin{matrix}1 & t>0\\ 0 & t=0\\ -1 & t<0 \end{matrix}\right.$

指数信号

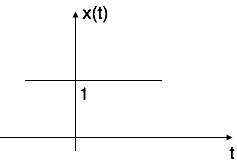
指数信号的形式为x(t) = $e^{\alpha t}$。

指数信号的形状由$\alpha$决定。

情况一：如果$\alpha$ = 0 $\to$ x(t) = $e^0$ = 1

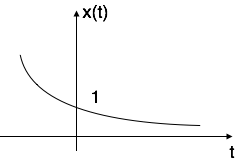
情况二：如果$\alpha$ < 0 即-ve 则x(t) = $e^{-\alpha t}$。形状称为衰减指数。

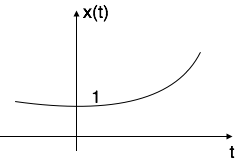
情况三：如果$\alpha$ > 0 即+ve 则x(t) = $e^{\alpha t}$。形状称为上升指数。

矩形信号

设其用x(t)表示，定义为

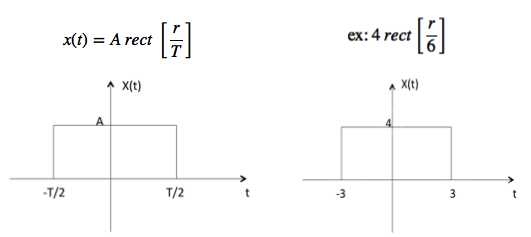
三角形信号

设其用x(t)表示

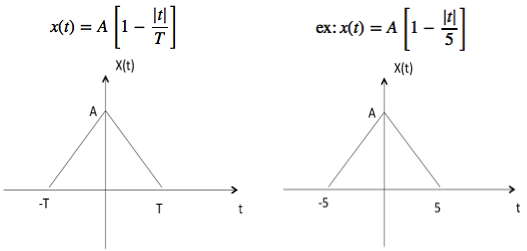
正弦信号

正弦信号的形式为x(t) = A cos(${w}_{0}\,\pm \phi$) 或 A sin(${w}_{0}\,\pm \phi$)

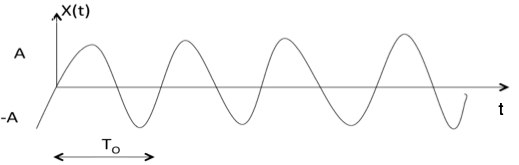
其中T₀ = $2\pi \over {w}_{0}$

Sinc函数

它用sinc(t)表示，定义为sinc

$$(t) = {sin \pi t \over \pi t}$$

$$= 0\, \text{对于t} = \pm 1, \pm 2, \pm 3 ...$$

采样函数

它用sa(t)表示，定义为

$$sa(t) = {sin t \over t}$$

$$= 0 \,\, \text{对于t} = \pm \pi,\, \pm 2 \pi,\, \pm 3 \pi \,...$$