信号分类

---

---

信号可分为以下几类：

• 连续时间信号和离散时间信号

• 确定性信号和非确定性信号

• 偶信号和奇信号

• 周期信号和非周期信号

• 能量信号和功率信号

• 实信号和虚信号

连续时间信号和离散时间信号

如果一个信号在所有时刻都有定义，则称其为连续信号。

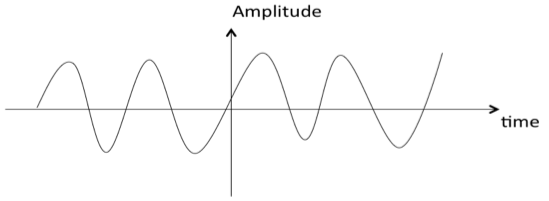
如果一个信号只在离散时刻定义，则称其为离散信号。

确定性信号和非确定性信号

如果在任何时刻关于信号的值没有不确定性，则称该信号为确定性信号。或者，可以用数学公式精确定义的信号称为确定性信号。

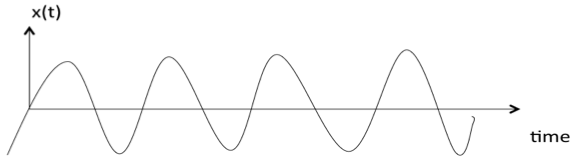
如果在某些时刻关于信号的值存在不确定性，则称该信号为非确定性信号。非确定性信号本质上是随机的，因此称为随机信号。随机信号无法用数学方程描述。它们是用概率术语建模的。

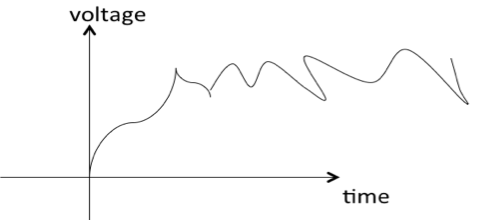
偶信号和奇信号

如果一个信号满足条件x(t) = x(-t)，则称其为偶信号。

例1：t2, t4… cost 等。

设x(t) = t2

x(-t) = (-t)2 = t2 = x(t)

$\therefore, $ t2是偶函数

例2：如下图所示，矩形函数x(t) = x(-t)，因此它也是偶函数。

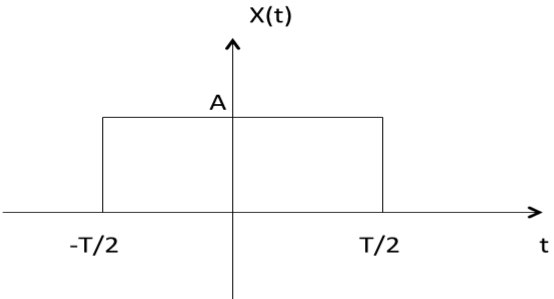
如果一个信号满足条件x(t) = -x(-t)，则称其为奇信号。

例：t, t3 ... 和 sin t

设x(t) = sin t

x(-t) = sin(-t) = -sin t = -x(t)

$\therefore, $ sin t是奇函数。

任何函数ƒ(t)都可以表示为其偶函数ƒ_e(t)和奇函数ƒ_o(t)的和。

ƒ(t ) = ƒ_e(t ) + ƒ₀(t )

其中

ƒ_e(t ) = ½[ƒ(t ) +ƒ(-t )]

周期信号和非周期信号

如果一个信号满足条件x(t) = x(t + T)或x(n) = x(n + N)，则称其为周期信号。

其中

T = 基波周期，

1/T = f = 基波频率。

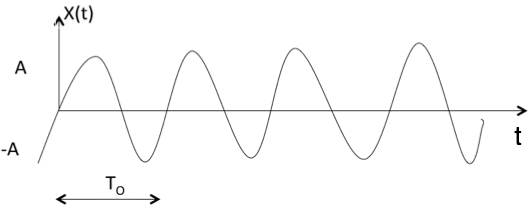
上述信号将每隔T₀时间间隔重复一次，因此它是周期为T₀的周期信号。

能量信号和功率信号

如果一个信号具有有限能量，则称其为能量信号。

$$\text{能量}\, E = \int_{-\infty}^{\infty} x^2\,(t)dt$$

如果一个信号具有有限功率，则称其为功率信号。

$$\text{功率}\, P = \lim_{T \to \infty}\,{1\over2T}\,\int_{-T}^{T}\,x^2(t)dt$$

注意：一个信号不能同时是能量信号和功率信号。此外，一个信号也可能既不是能量信号也不是功率信号。

能量信号的功率 = 0

功率信号的能量 = ∞

实信号和虚信号

如果一个信号满足条件x(t) = x*(t)，则称其为实信号。

如果一个信号满足条件x(t) = -x*(t)，则称其为奇信号 (此处应为虚信号，原文有误)。

例子

如果x(t)= 3，则x*(t)=3*=3，这里x(t)是实信号。

如果x(t)= 3j，则x*(t)=3j* = -3j = -x(t)，因此x(t)是虚信号。

注意：对于实信号，虚部应为零。类似地，对于虚信号，实部应为零。