信号基本运算

---

---

一般来说，有两个变量参数

1. 幅度
2. 时间

以下运算可以对幅度进行

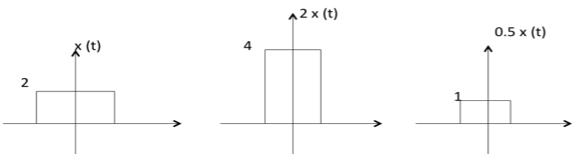
幅度缩放

C x(t) 是 x(t) 的幅度缩放版本，其幅度按因子 C 缩放。

加法

两个信号的加法就是它们对应幅度的加法。这可以用以下示例最好地解释

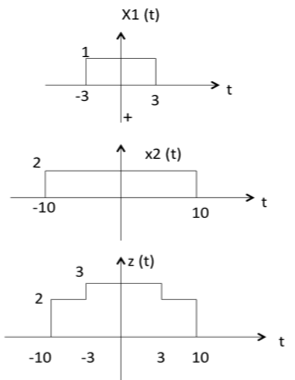
从上图可以看出，

-10 < t < -3 时，z(t) 的幅度 = x1(t) + x2(t) = 0 + 2 = 2

-3 < t < 3 时，z(t) 的幅度 = x1(t) + x2(t) = 1 + 2 = 3

3 < t < 10 时，z(t) 的幅度 = x1(t) + x2(t) = 0 + 2 = 2

减法

两个信号的减法就是它们对应幅度的减法。这可以用以下示例最好地解释

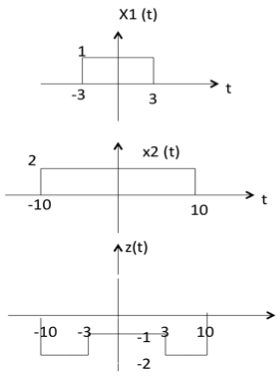
从上图可以看出，

-10 < t < -3 时，z(t) 的幅度 = x1(t) - x2(t) = 0 - 2 = -2

-3 < t < 3 时，z(t) 的幅度 = x1(t) - x2(t) = 1 - 2 = -1

3 < t < 10 时，z(t) 的幅度 = x1(t) + x2(t) = 0 - 2 = -2

乘法

两个信号的乘法就是它们对应幅度的乘法。这可以用以下示例最好地解释

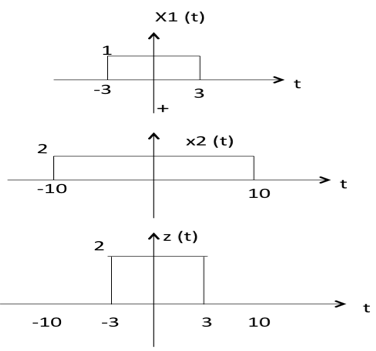
从上图可以看出，

-10 < t < -3 时，z(t) 的幅度 = x1(t) ×x2(t) = 0 ×2 = 0

-3 < t < 3 时，z(t) 的幅度 = x1(t) ×x2(t) = 1 ×2 = 2

3 < t < 10 时，z(t) 的幅度 = x1(t) × x2(t) = 0 × 2 = 0

以下运算可以对时间进行

时间移位

x(t $\pm$ t₀) 是信号 x(t) 的时间移位版本。

x (t + t₀) $\to$ 负移位

x (t - t₀) $\to$ 正移位

时间缩放

x(At) 是信号 x(t) 的时间缩放版本，其中 A 始终为正。

|A| > 1 $\to$ 信号压缩

|A| < 1 $\to$ 信号扩展

注意：u(at) = u(t) 时间缩放不适用于单位阶跃函数。

时间反转

x(-t) 是信号 x(t) 的时间反转。