信号分析

---

---

向量与信号的类比

向量和信号之间存在完美的类比。

向量

向量包含大小和方向。向量的名称用粗体表示，其大小用普通字体表示。

例如：V是一个大小为V的向量。考虑两个向量V₁和V₂，如下面的图所示。设V₁沿V₂的分量为C₁₂V₂。可以通过从V₁的末端向V₂作垂线得到一个向量V₁沿向量V₂的分量，如图所示

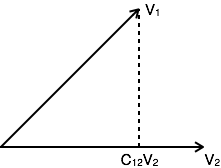
向量V₁可以用向量V₂表示

V₁= C₁₂V₂ + V_e

其中Ve是误差向量。

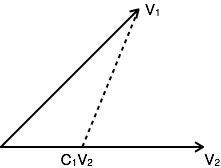
但这并不是用V₂表示向量V₁的唯一方法。其他的可能性是

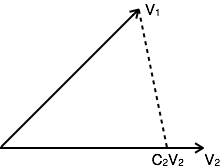
对于较大的分量值，误差信号最小。如果C₁₂=0，则这两个信号被称为正交。

两个向量的点积

V₁ . V₂ = V₁.V₂ cosθ

θ = V1和V2之间的角度

V₁ . V₂ =V₂.V₁

V₁沿V₂的分量 = V₁ Cos θ = $V1.V2 \over V2$

从图中，V₁沿V₂的分量 = C ₁₂ V₂

$$V_1.V_2 \over V_2 = C_12\,V_2$$

$$ \Rightarrow C_{12} = {V_1.V_2 \over V_2}$$

信号

正交的概念可以应用于信号。让我们考虑两个信号f₁(t)和f₂(t)。与向量类似，可以用f₂(t)近似表示f₁(t)，如下所示

f₁(t) = C₁₂ f₂(t) + f_e(t) 对于(t₁ < t < t₂)

$ \Rightarrow $ f_e(t) = f₁(t) – C₁₂ f₂(t)

一种可能的最小化误差的方法是在区间t₁到t₂上进行积分。

$${1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [f_e (t)] dt$$

$${1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [f_1(t) - C_{12}f_2(t)]dt $$

但是，此步骤也不能将误差降低到明显的程度。这可以通过取误差函数的平方来纠正。

$\varepsilon = {1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [f_e (t)]^2 dt$

$\Rightarrow {1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [f_e (t) - C_{12}f_2]^2 dt $

其中ε是误差信号的均方值。要计算使误差最小的C₁₂的值，需要计算${d\varepsilon \over dC_{12} } = 0 $

$\Rightarrow {d \over dC_{12} } [ {1 \over t_2 - t_1 } \int_{t_1}^{t_2} [f_1 (t) - C_{12} f_2 (t)]^2 dt]= 0 $

$\Rightarrow {1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [ {d \over dC_{12} } f_{1}^2(t) - {d \over dC_{12} } 2f_1(t)C_{12}f_2(t)+ {d \over dC_{12} } f_{2}^{2} (t) C_{12}^2 ] dt =0 $

不包含C12项的项的导数为零。

$\Rightarrow \int_{t_1}^{t_2} - 2f_1(t) f_2(t) dt + 2C_{12}\int_{t_1}^{t_2}[f_{2}^{2} (t)]dt = 0 $

如果 $C_{12} = {{\int_{t_1}^{t_2}f_1(t)f_2(t)dt } \over {\int_{t_1}^{t_2} f_{2}^{2} (t)dt }} $ 分量为零，则这两个信号被称为正交。

令C₁₂ = 0得到正交条件。

0 = $ {{\int_{t_1}^{t_2}f_1(t)f_2(t)dt } \over {\int_{t_1}^{t_2} f_{2}^{2} (t)dt }} $

$$ \int_{t_1}^{t_2} f_1 (t)f_2(t) dt = 0 $$

正交向量空间

一组完整的正交向量称为正交向量空间。考虑一个三维向量空间，如下所示

考虑一点(X₁, Y₁, Z₁)处的向量A。考虑三个单位向量(V_X, V_Y, V_Z)，分别沿X、Y、Z轴方向。由于这些单位向量是相互正交的，因此满足

$$V_X. V_X= V_Y. V_Y= V_Z. V_Z = 1 $$

$$V_X. V_Y= V_Y. V_Z= V_Z. V_X = 0 $$

可以将上述条件写成

$$V_a . V_b = \left\{ \begin{array}{l l} 1 & \quad a = b \\ 0 & \quad a \neq b \end{array} \right. $$

向量A可以用其分量和单位向量表示为

$A = X_1 V_X + Y_1 V_Y + Z_1 V_Z................(1) $

这个三维空间中的任何向量都可以仅用这三个单位向量表示。

如果考虑n维空间，则该空间中的任何向量A都可以表示为

$ A = X_1 V_X + Y_1 V_Y + Z_1 V_Z+...+ N_1V_N.....(2) $

由于任何向量A的单位向量的大小为1

A沿x轴的分量 = A.V_X

A沿Y轴的分量 = A.V_Y

A沿Z轴的分量 = A.V_Z

类似地，对于n维空间，A沿某个G轴的分量

$= A.VG...............(3)$

将公式2代入公式3。

$\Rightarrow CG= (X_1 V_X + Y_1 V_Y + Z_1 V_Z +...+G_1 V_G...+ N_1V_N)V_G$

$= X_1 V_X V_G + Y_1 V_Y V_G + Z_1 V_Z V_G +...+ G_1V_G V_G...+ N_1V_N V_G$

$= G_1 \,\,\,\,\, \text{因为 } V_G V_G=1$

$如果 V_G V_G \neq 1 \,\,\text{即} V_G V_G= k$

$AV_G = G_1V_G V_G= G_1K$

$G_1 = {(AV_G) \over K}$

正交信号空间

让我们考虑一组n个在区间t₁到t₂上相互正交的函数x₁(t)，x₂(t)... x_n(t)。由于这些函数彼此正交，因此任何两个信号x_j(t)，x_k(t)必须满足正交条件。即

$$\int_{t_1}^{t_2} x_j(t)x_k(t)dt = 0 \,\,\, \text{其中}\, j \neq k$$

$$\text{令} \int_{t_1}^{t_2}x_{k}^{2}(t)dt = k_k $$

令一个函数f(t)，可以通过沿相互正交的信号添加分量来用这个正交信号空间进行近似，即

$\,\,\,f(t) = C_1x_1(t) + C_2x_2(t) + ... + C_nx_n(t) + f_e(t) $

$\quad\quad=\Sigma_{r=1}^{n} C_rx_r (t) $

$\,\,\,f(t) = f(t) - \Sigma_{r=1}^n C_rx_r (t) $

均方误差 $ \varepsilon = {1 \over t_2 - t_2 } \int_{t_1}^{t_2} [ f_e(t)]^2 dt$

$$ = {1 \over t_2 - t_2 } \int_{t_1}^{t_2} [ f[t] - \sum_{r=1}^{n} C_rx_r(t) ]^2 dt $$

可以通过以下方式找到使均方误差最小化的分量

$$ {d\varepsilon \over dC_1} = {d\varepsilon \over dC_2} = ... = {d\varepsilon \over dC_k} = 0 $$

让我们考虑${d\varepsilon \over dC_k} = 0 $

$${d \over dC_k}[ {1 \over t_2 - t_1} \int_{t_1}^{t_2} [ f(t) - \Sigma_{r=1}^n C_rx_r(t)]^2 dt] = 0 $$

所有不包含C_k的项都为零。即在求和中，r=k项保留，所有其他项都为零。

$$\int_{t_1}^{t_2} - 2 f(t)x_k(t)dt + 2C_k \int_{t_1}^{t_2} [x_k^2 (t)] dt=0 $$

$$\Rightarrow C_k = {{\int_{t_1}^{t_2}f(t)x_k(t)dt} \over {int_{t_1}^{t_2} x_k^2 (t)dt}} $$

$$\Rightarrow \int_{t_1}^{t_2} f(t)x_k(t)dt = C_kK_k $$

均方误差

误差函数f_e(t)的平方平均值称为均方误差。用ε（epsilon）表示。

.

$\varepsilon = {1 \over t_2 - t_1 } \int_{t_1}^{t_2} [f_e (t)]^2dt$

$\,\,\,\,= {1 \over t_2 - t_1 } \int_{t_1}^{t_2} [f_e (t) - \Sigma_{r=1}^n C_rx_r(t)]^2 dt $

$\,\,\,\,= {1 \over t_2 - t_1 } [ \int_{t_1}^{t_2} [f_e^2 (t) ]dt + \Sigma_{r=1}^{n} C_r^2 \int_{t_1}^{t_2} x_r^2 (t) dt - 2 \Sigma_{r=1}^{n} C_r \int_{t_1}^{t_2} x_r (t)f(t)dt$

知道 $C_{r}^{2} \int_{t_1}^{t_2} x_r^2 (t)dt = C_r \int_{t_1}^{t_2} x_r (t)f(d)dt = C_r^2 K_r $

$\varepsilon = {1 \over t_2 - t_1 } [ \int_{t_1}^{t_2} [f^2 (t)] dt + \Sigma_{r=1}^{n} C_r^2 K_r - 2 \Sigma_{r=1}^{n} C_r^2 K_r] $

$\,\,\,\,= {1 \over t_2 - t_1 } [\int_{t_1}^{t_2} [f^2 (t)] dt - \Sigma_{r=1}^{n} C_r^2 K_r ] $

$\, \therefore \varepsilon = {1 \over t_2 - t_1 } [\int_{t_1}^{t_2} [f^2 (t)] dt + (C_1^2 K_1 + C_2^2 K_2 + ... + C_n^2 K_n)] $

上述公式用于评估均方误差。

封闭且完整的正交函数集

让我们考虑一组n个在区间t₁到t₂上相互正交的函数x₁(t)，x₂(t)...x_n(t)。当不存在满足条件$\int_{t_1}^{t_2} f(t)x_k(t)dt = 0 $的函数f(t)时，这称为封闭且完整的集合。

如果此函数满足方程$\int_{t_1}^{t_2} f(t)x_k(t)dt=0 \,\, \text{对于}\, k = 1,2,..$，则f(t)被称为与正交集中的每个函数正交。如果没有f(t)，则此集合是不完整的。当包含f(t)时，它成为封闭且完整的集合。

可以通过沿相互正交的信号添加分量来用此正交集近似f(t)，即

$$f(t) = C_1 x_1(t) + C_2 x_2(t) + ... + C_n x_n(t) + f_e(t) $$

如果无限级数$C_1 x_1(t) + C_2 x_2(t) + ... + C_n x_n(t)$收敛到f(t)，则均方误差为零。

复函数中的正交性

如果f₁(t)和f₂(t)是两个复函数，则f₁(t)可以用f₂(t)表示为

$f_1(t) = C_{12}f_2(t) \,\,\,\,\,\,\,\,$ ..误差可忽略不计

其中 $C_{12} = {{\int_{t_1}^{t_2} f_1(t)f_2^*(t)dt} \over { \int_{t_1}^{t_2} |f_2(t)|^2 dt}} $

其中 $f_2^* (t)$ = f₂(t)的共轭复数。

如果f₁(t)和f₂(t)正交，则C₁₂ = 0

$$ {\int_{t_1}^{t_2} f_1 (t) f_2^*(t) dt \over \int_{t_1}^{t_2} |f_2 (t) |^2 dt} = 0 $$

$$\Rightarrow \int_{t_1}^{t_2} f_1 (t) f_2^* (dt) = 0$$

上述公式表示复函数中的正交条件。