采样定理

定理：连续时间信号可以由其样本表示，当采样频率 f_s 大于或等于消息信号最高频率分量的两倍时，可以恢复原始信号。即

$$ f_s \geq 2 f_m. $$

证明：考虑一个连续时间信号 x(t)。x(t) 的频谱限于 f_m Hz，即 x(t) 的频谱在 |ω|＞ω_m 时为零。

输入信号 x(t) 的采样可以通过将 x(t) 与周期为 T_s 的冲激串 δ(t) 相乘来获得。乘法器的输出是一个离散信号，称为采样信号，在下图中用 y(t) 表示。

在这里，您可以观察到采样信号采用冲激的周期。采样过程可以用以下数学表达式解释

$ \text{采样信号}\, y(t) = x(t) \cdot \delta(t) \,\,...\,...(1) $

δ(t) 的三角傅里叶级数表示为

$ \delta(t)= a_0 + \sum_{n=1}^{\infty}(a_n \cos⁡ n\omega_s t + b_n \sin⁡ n\omega_s t )\,\,...\,...(2) $

其中 $ a_0 = \frac{1}{T_s} \int_{-T/2}^{T/2} \delta (t)dt = \frac{1}{T_s} \delta(0) = \frac{1}{T_s} $

$ a_n = \frac{2}{T_s} \int_{-T/2}^{T/2} \delta (t) \cos n\omega_s t \, dt = \frac{2}{T_s} \delta (0) \cos n \omega_s 0 = \frac{2}{T_s} $

$b_n = \frac{2}{T_s} \int_{-T/2}^{T/2} \delta(t) \sin⁡ n\omega_s t\, dt = \frac{2}{T_s} \delta(0) \sin⁡ n\omega_s 0 = 0 $

将以上值代入公式 2。

$\therefore\, \delta(t)= \frac{1}{T_s} + \sum_{n=1}^{\infty} ( \frac{2}{T_s} \cos ⁡ n\omega_s t+0)$

将 δ(t) 代入公式 1。

$\to y(t) = x(t) \cdot \delta(t) $

$ = x(t) [\frac{1}{T_s} + \sum_{n=1}^{\infty}(\frac{2}{T_s} \cos n\omega_s t) ] $

$ = \frac{1}{T_s} [x(t) + 2 \sum_{n=1}^{\infty} (\cos n\omega_s t) x(t) ] $

$ y(t) = \frac{1}{T_s} [x(t) + 2\cos \omega_s t \cdot x(t) + 2 \cos 2\omega_s t \cdot x(t) + 2 \cos 3\omega_s t \cdot x(t) \,...\, ...\,] $

对两边进行傅里叶变换。

$Y(\omega) = \frac{1}{T_s} [X(\omega)+X(\omega-\omega_s )+X(\omega+\omega_s )+X(\omega-2\omega_s )+X(\omega+2\omega_s )+ \,...] $

$\therefore\,\, Y(\omega) = \frac{1}{T_s} \sum_{n=-\infty}^{\infty} X(\omega - n\omega_s )\quad\quad where \,\,n= 0,\pm1,\pm2,... $

为了重建 x(t)，必须从采样信号频谱 Y(ω) 中恢复输入信号频谱 X(ω)，当 Y(ω) 的周期之间没有重叠时，这是可能的。

以下图表给出了不同条件下采样频率频谱的可能性。

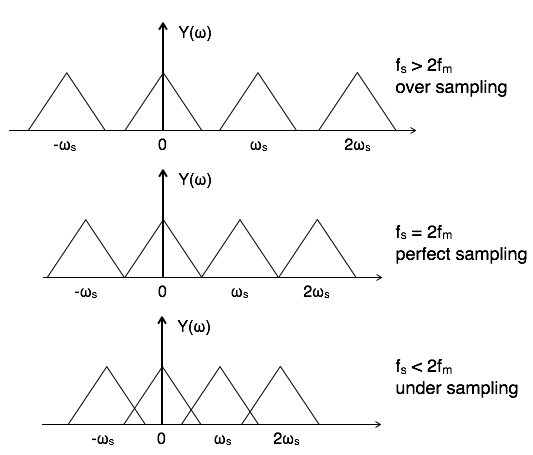
混叠效应

欠采样情况下重叠区域表示混叠效应，可以通过以下方法消除：

• 考虑 f_s > 2f_m

• 使用抗混叠滤波器。