宇宙学 - 暗能量

暗能量领域在天文学中是一个非常模糊的领域，因为它在所有方程中都是一个自由参数，但我们对其究竟是什么却没有明确的概念。

我们将从弗里德曼方程开始，

$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2}$$

大多数关于宇宙学的入门书籍，它们都从描述哈勃观测之前，宇宙是封闭且静态的这一情景开始来介绍暗能量。

现在，为了使宇宙保持静态，等式右侧的两个项必须相等且都为零。但如果第一项大于第二项，那么宇宙将不会是静态的。因此，爱因斯坦将自由参数∧引入场方程以使宇宙保持静态。他认为，无论第一项与第二项相比如何，只要方程中存在另一个分量，就可以始终得到一个静态的宇宙，该分量可以补偿这两个项之间的差异。

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2} + \frac{\wedge}{3}$$

$$\left ( \frac{\ddot{a}}{a} \right ) = -\frac{4 \pi G}{3}\left ( \rho + \frac{3P}{c^2} \right ) + \frac{\wedge}{3}$$

其中$P = \rho \ast c^2/3$ 和 $\wedge = \rho \ast c^2$ 是宇宙学常数。（负号仅仅是因为引力是吸引的）

在上式（加速度方程）中 -

第三项起到排斥力的作用，因为方程的另一部分是吸引的。

该方程的物理意义在于˙a = 0，因为当时没有任何证据表明宇宙正在膨胀。如果这两个项不匹配，那么最好添加一个分量，并且根据偏移量，我们始终可以更改自由参数的值。

当时对这个宇宙学常数没有物理解释，这就是为什么当宇宙膨胀的解释在1920年代被发现时，爱因斯坦立即不得不抛弃这个常数。

这个宇宙学常数的解释仍在使用，因为它解释了宇宙的不同版本，但是这个宇宙学常数的定义，其解释方式随着时间的推移而不断变化。

现在，出于许多原因，宇宙学常数的概念已被重新引入宇宙学。其中一个原因是，我们对宇宙不同成分（重子物质、暗物质、辐射）的能量密度进行了观测，因此我们知道这个参数是什么。使用宇宙微波背景辐射进行的独立观测表明k=0。

$$CMB, k=0\: \rho = \rho_c = \frac{3H_0^2}{8\pi G} \approx 10 \: 氢原子.m^{-3}$$

为了使k为0，ρ必须等于ρc，但如果我们把我们知道的所有东西加起来，它并不等于0，这意味着存在某个其他分量，表明它远小于ρc。

$$\rho = \rho_b + \rho_{DM} + \rho_{rad} << \rho_c$$

暗能量的另一个证据来自Ia型超新星观测，当白矮星吸积物质并超过钱德拉塞卡极限时发生Ia型超新星爆发，这是一个非常精确的极限（≈ 1.4M）。现在，每次发生Ia型超新星爆发时，我们都具有相同的质量，这意味着系统的总结合能相同，并且我们所能看到的光能也相同。

当然，超新星的光会先增强然后减弱，但是如果你测量峰值亮度，它总是相同的，这使其成为一个标准的观测对象。因此，借助Ia型超新星，我们用来测量宇宙的宇宙学成分，天文学家发现，高红移的超新星比低红移的超新星暗30％-40％，如果存在任何非零∧项，则可以解释这一点。

在宇宙学模型中，DE（暗能量）被视为一种流体，这意味着我们可以写出它的状态方程。状态方程是连接物质两种不同状态的变量（如压强、密度、温度和体积）的方程。

从量纲上看，

$$\frac{8 \pi G}{3}\rho = \frac{\wedge}{3}$$

$$\rho_\wedge = \frac{\wedge}{8\pi G}$$

DE的能量密度，

$$\epsilon_\wedge = \rho_\wedge \ast c^2 = \frac{\wedge c^2}{8 \pi G}$$

暗能量密度参数，

$$\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$$

Ω∧是暗能量密度相对于临界密度的值。

$$\rho = \rho_b + \rho_{DM} +\rho_\wedge$$

关于暗能量，有很多理论，它正在排斥宇宙并导致宇宙膨胀。一个假设是，这种暗能量可能是真空能量密度。假设空间本身正在处理一些能量，当你在空间的单位体积内计算重子物质、暗物质和辐射的量时，你也在计算与空间相关的能量的量，但尚不清楚暗能量是否真的是真空能量密度。

我们知道暗物质和辐射的密度与尺度因子之间的关系是，

$$\rho_m \propto \frac{1}{a^3}$$

$$\rho_m \propto \frac{1}{a^4}$$

我们绘制了密度与尺度因子的关系图。在同一张图中，我们可以看到ρ∧随着宇宙的膨胀保持不变，它不依赖于尺度因子。

下图显示了密度与尺度因子之间的关系。

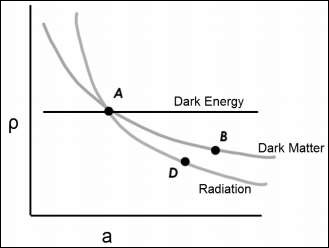
‘ρ’与‘a’（尺度因子与时间相关）在同一张图中，暗能量被建模为一个常数。因此，无论我们在当前宇宙中测量到多少暗能量，它都是一个常数。

要点

打印页面