宇宙学 - 径向速度法

在上一章中，讨论了轨道平面和天球平面垂直的圆形轨道情况下的径向速度法。在这里，我们处理另一种情况，即圆形轨道的轨道平面和天球平面不垂直。

当轨道平面相对于天球平面成一定角度（不垂直）时，我们有以下情况：

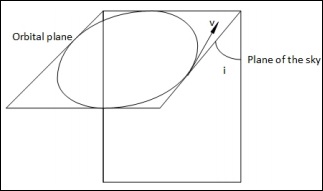
在这种情况下，当它们垂直时，我们有两个点可以测量真实速度。但在这里，这是不可能的。在所有点，我们只能测量真实速度v的一个分量。

$$v_r = v \:sin(i)cos(\theta)$$

其中θ是轨道的相位，是一个时间相关的量。另一方面，倾角i与时间无关。因此，

$$(v_r)_{max} = v\: sin(i)$$

观察到的径向速度曲线将具有以下形式：

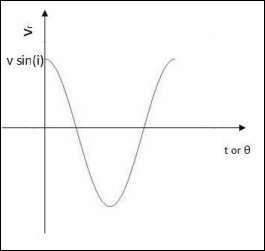
当轨道平面垂直于天空时：

$$m_p = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}}(M_\ast)^{\frac{2}{3}}v$$

其中m_p, P, G, M∗分别表示行星质量、轨道周期、万有引力常数和恒星质量。但在这种情况下，我们应该将其修改如下：

$$m_psin(i) = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}} (M_\ast)^{\frac{2}{3}}(v_r)_{max}$$

但是，找到i的值是一项困难的任务。我们可以使用凌日法对i的值施加某些约束。行星在恒星和地球之间通过的过程称为凌日。我们可以通过观察凌日来获得光变曲线，光变曲线中观察到的光通量的显着下降意味着i接近90度。如果未满足此类条件，我们无法对i的值有任何了解。然后我们找到的m_p值可以作为行星质量的下限，因为它实际上是m_p sin(i)，并且sin(i) ≤ 1。

总之，径向速度法比凌日法更方便，因为径向速度可以随时测量，而凌日测量只能在凌日期间进行，而凌日持续时间可能不长。

要点

• 径向速度法无法确定行星轨道倾角。

• 径向速度法优于凌日法，因为径向速度始终可以测量，而凌日则不然。

• 凌日是短暂的，很容易错过。