
- 宇宙学教程
- 宇宙学 - 首页
- 膨胀宇宙
- 造父变星
- 红移和退行速度
- 红移与运动学多普勒频移
- 宇宙度规与膨胀
- 罗伯逊-沃尔克度规
- 哈勃参数与比例因子
- 弗里德曼方程与宇宙模型
- 流体方程
- 物质主导宇宙
- 辐射主导宇宙
- 暗能量
- 螺旋星系旋转曲线
- 星系速度弥散测量
- 哈勃参数与密度参数
- 宇宙年龄
- 角直径距离
- 光度距离
- Ia型超新星
- 宇宙微波背景辐射
- CMB - 解耦时的温度
- CMB辐射的各向异性与COBE卫星
- CMB各向异性的模型
- 最后散射面上的视界长度
- 太阳系外行星探测
- 径向速度法
- 凌日法
- 系外行星特性
- 宇宙学有用资源
- 宇宙学速成指南
- 宇宙学 - 有用资源
- 宇宙学 - 讨论
宇宙学速成指南
宇宙学 - 膨胀宇宙
宇宙学是研究宇宙的学科。追溯到过去,关于宇宙起源存在着几种不同的学派。许多学者相信稳态理论。根据这一理论,宇宙始终保持不变,它没有开端。
而另一部分人则相信大爆炸理论。这一理论预测了宇宙的开端。有证据表明大爆炸留下了热的残余辐射,这再次支持了该模型。大爆炸理论预测了宇宙中轻元素的丰度。因此,遵循著名的大爆炸模型,我们可以说宇宙有一个开端。我们生活在一个膨胀的宇宙中。
哈勃红移
在20世纪初,最先进的望远镜,威尔逊山天文台的100英寸望远镜,是当时最大的望远镜。哈勃是使用该望远镜工作的杰出科学家之一。他发现银河系外还有星系。河外天文学只有100年的历史。威尔逊山天文台是最大的望远镜,直到帕洛马山天文台建成,拥有200英寸的望远镜。
哈勃并不是唯一一个观测到银河系外星系的科学家,休马森帮助了他。他们开始测量附近星系的频谱。然后他们观察到星系光谱在可见波长范围内有连续发射。在连续谱的顶部有发射线和吸收线。从这些谱线,我们可以估计星系是远离我们还是靠近我们。
当我们得到一个光谱时,我们假设最强烈的谱线来自H-α。根据文献,最强烈的谱线应该出现在6563 Å,但如果谱线出现在7000Å附近,我们可以很容易地说它是红移的。
根据狭义相对论,
$$1 + z = \sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}$$
其中,Z是红移,一个无量纲数,v是退行速度。
$$\frac{\lambda_{obs}}{\lambda_{rest}} = 1 + z$$
哈勃和休马森在他们的论文中列出了22个星系。几乎所有这些星系都表现出红移。他们绘制了速度(km/s)与距离(Mpc)的关系图。他们观察到了一种线性趋势,哈勃提出了他著名的定律如下。
$$v_r = H_o d$$
这是哈勃红移距离关系。下标r表示膨胀是径向的。其中,$v_r$是退行速度,$H_o$是哈勃参数,d是星系到我们的距离。他们得出结论:如果宇宙的膨胀速度是均匀的,那么远离我们的星系退行速度越快。
膨胀
一切都在远离我们。星系不是静止的,总有一些膨胀的谐波。哈勃参数的单位是km sec−1Mpc−1。如果距离为-1 Mpc,星系将以200 kms/sec的速度移动。哈勃参数给了我们膨胀的速度。根据哈勃和休马森的研究,$H_o$的值为200 kms/sec/Mpc。
数据显示所有星系都在远离我们。因此,很明显我们位于宇宙的中心。但哈勃并没有犯这个错误,在他看来,无论我们生活在哪个星系,我们都会发现所有其他星系都在远离我们。因此,结论是星系之间的空间膨胀,宇宙没有中心。
膨胀发生在任何地方。然而,有一些力正在对抗膨胀。化学键、万有引力和其他的吸引力将物体结合在一起。早期所有物体都靠得很近。考虑到大爆炸是一种冲量力,这些物体开始彼此远离。
时间尺度
在局部尺度上,动力学受引力支配。在最初的哈勃定律中,有一些星系显示出蓝移。这可以归因于星系的组合引力势。引力使一些事物脱离了哈勃定律。仙女座星系正在向我们靠近。引力试图减慢速度。最初膨胀正在减慢,现在正在加速。
由于这个原因,出现了一个宇宙急转弯。对哈勃参数进行了几次估计。在90年中,它从500 kms/sec/Mpc发展到69 kms/sec/Mpc。值的差异是由于距离的低估。造父变星被用作距离校准器,但是有不同类型的造父变星,在估计哈勃参数时没有考虑这一事实。
哈勃时间
哈勃常数给了我们对宇宙年龄的现实估计。如果星系一直以相同的速度运动,则$H_o$将给出宇宙的年龄。$H_o$的倒数给了我们哈勃时间。
$$t_H = \frac{1}{H_o}$$
用$H_o$的当前值替换,$t_H$ = 140亿年。从宇宙开始以来,膨胀速度一直保持不变。即使事实并非如此,$H_o$也为宇宙的年龄提供了一个有用的上限。假设膨胀速度恒定,当我们绘制距离和时间之间的关系图时,图的斜率由速度给出。
在这种情况下,哈勃时间等于实际时间。然而,如果宇宙过去膨胀得更快,现在膨胀得更慢,那么哈勃时间给出了宇宙年龄的上限。如果宇宙以前膨胀得较慢,现在正在加速,那么哈勃时间将给出宇宙年龄的下限。
$t_H = t_{age}$ − 如果膨胀速度恒定。
$t_H > t_{age}$ − 如果宇宙过去膨胀得更快,现在膨胀得更慢。
$t_H < t_{age}$ − 如果宇宙过去膨胀得更慢,现在膨胀得更快。
考虑一组10个星系,它们与另一组星系的距离为200 Mpc。星系团内的星系永远不会认为宇宙正在膨胀,因为局部星系团内的动力学受引力支配。
要点
宇宙学是研究我们宇宙过去、现在和未来的学科。
我们的宇宙大约有140亿年的历史。
宇宙正在不断膨胀。
哈勃参数是衡量宇宙年龄的指标。
Ho的当前值为69 kms/sec/Mpc。
宇宙学 - 造父变星
很长一段时间内,没有人认为银河系外存在星系。1924年,埃德温·哈勃在仙女座星云中探测到造父变星并估计了它们的距离。他得出结论,这些“螺旋星云”实际上是其他星系,而不是我们银河系的一部分。因此,他确定M31(仙女座星系)是一个岛宇宙。这是河外天文学的诞生。
造父变星表现出周期性的亮度下降。观测表明,连续下降之间的时间间隔(称为脉动周期)与光度有关。因此,它们可以用作距离指示器。像太阳这样的主序星处于流体静力平衡状态,它们在其核心燃烧氢。氢完全燃烧后,恒星向红巨星阶段移动,并试图恢复其平衡。
造父变星是主序星之后,正在从主序星向红巨星过渡的恒星。
造父变星的分类
这些脉动变星主要分为3类:
I型造父变星(或经典造父变星)− 周期为30-100天。
II型造父变星(或室女座W型星)− 周期为1-50天。
天琴座RR型变星 − 周期为0.1-1天。
当时,哈勃不知道这种变星的分类。这就是为什么哈勃常数被高估的原因,因此他估计了我们宇宙的较低年龄。因此,退行速度也被高估了。在造父变星中,扰动从恒星中心径向向外传播,直到达到新的平衡。
亮度和脉动周期之间的关系
现在让我们尝试理解这样一个事实的物理基础:更高的脉动周期意味着更高的亮度。考虑一颗光度为L,质量为M的恒星。
我们知道:
$$L \propto M^\alpha$$
其中,对于低质量恒星,α = 3到4。
根据斯特藩-玻尔兹曼定律,我们知道:
$$L \propto R^2 T^4$$
如果R是半径,$c_s$是声速,那么脉动周期P可以写成:
$$P = R/c_s$$
但是,任何介质中的声速都可以用温度表示为:
$$c_s = \sqrt{\frac{\gamma P}{\rho}}$$
这里,对于等温情况,γ 为 1。
对于理想气体,P = nkT,其中 k 为玻尔兹曼常数。因此,我们可以写成:
$$P = \frac{\rho kT}{m}$$
其中 ρ 为密度,m 为质子的质量。
因此,周期由下式给出:
$$P \cong \frac{Rm^{\frac{1}{2}}}{(kT)^{{\frac{1}{2}}}}$$
维里定理指出,对于稳定、自引力、球形分布的等质量物体(如恒星、星系),物体的总动能k等于总引力势能u的负二分之一,即:
$$u = -2k$$
让我们假设维里定理对这些变星成立。如果我们考虑一颗恒星表面上的质子,那么根据维里定理,我们可以说:
$$\frac{GMm}{R} = mv^2$$
根据麦克斯韦分布:
$$v = \sqrt{\frac{3kT}{2}}$$
因此,周期:
$$P \sim \frac{RR^{\frac{1}{2}}}{(GM)^{\frac{1}{2}}}$$
这意味着
$$P \propto \frac{R^{\frac{3}{2}}}{M^{\frac{1}{2}}}$$
我们知道 – $M \propto L^{1/\alpha}$
还有 $R \propto L^{1/2}$
因此,对于β > 0,我们最终得到 – $P \propto L^\beta$
要点
造父变星是主序后恒星,它们正在从主序星转变为红巨星。
造父变星分为三种类型:I 型、II 型和 RR Lyrae 型,其脉动周期依次递减。
造父变星的脉动周期与其亮度(光度)成正比。
红移和退行速度
哈勃的观测利用了径向速度与谱线位移相关的这一事实。在这里,我们将观察四种情况,并找到退行速度($v_r$)和红移 (z) 之间的关系。
情况 1:运动源的非相对论性情况
在这种情况下,v远小于c。光源正在发射某种信号(声音、光等),该信号以波阵面的形式传播。在源参考系中,连续两个信号之间的时间间隔为Δts。在观察者参考系中,连续两个信号之间的时间间隔为Δto。
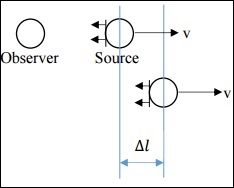
如果观察者和光源都是静止的,那么 Δts = Δto,但这里并非如此。相反,关系如下。
$$\Delta t_o = \Delta t_s + \frac{\Delta l}{c}$$
现在,$\Delta l = v \Delta t_s$
此外,由于(波速 × 时间)= 波长,我们得到
$$\frac{\Delta t_o}{\Delta t_s} = \frac{\lambda_o}{\lambda_s}$$
根据以上等式,我们得到以下关系:
$$\frac{\lambda_o}{\lambda_s} = 1 + \frac{v}{c}$$
其中 $\lambda _s$ 是光源处信号的波长,$\lambda _o$ 是观察者解释的信号的波长。
在这里,由于光源正在远离观察者,因此v为正。
红移:
$$z = \frac{\lambda_o - \lambda_s}{\lambda_s} = \frac{\lambda_o}{\lambda_s} - 1$$
根据以上等式,我们得到如下红移:
$$z = \frac{v}{c}$$
情况 2:运动观察者的非相对论性情况
在这种情况下,v远小于c。这里,$\Delta l$不同。
$$\Delta l = v \Delta t_o$$
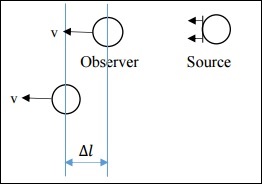
简化后,我们得到:
$$\frac{\Delta t_o}{\Delta t_s} = \left ( 1 - \frac{v}{c} \right )^{-1}$$
我们得到如下红移:
$$z = \frac{v/c}{1-v/c}$$
由于v << c,情况 I 和情况 II 的红移表达式近似相同。
让我们看看上面两种情况下获得的红移有何不同。
$$z_{II} - z_I = \frac{v}{c} \left [ \frac{1}{1 - v/c}-1 \right ]$$
因此,由于 $(v/c)^2$ 项,$z_{II} − z_{I}$ 是一个非常小的数。
这意味着,如果 v << c,我们无法判断是光源在运动,还是观察者在运动。
现在让我们了解狭义相对论 (STR) 的基础:
光速是一个常数。
当光源(或观察者)以与光速相当的速度运动时,就会观察到相对论效应。
时间膨胀:$\Delta t_o = \gamma \Delta t_s$
长度收缩:$\Delta l_o = \Delta t_s/\gamma$
这里,γ 是洛伦兹因子,大于 1。
$$\gamma = \frac{1}{\sqrt{1-(v^2/c^2)}}$$
情况 3:运动光源的相对论性情况
在这种情况下,v与c相当。参考与情况 I 相同的图。由于相对论效应,观察到时间膨胀,因此得到以下关系。(光源以相对论速度运动)
$$\Delta t_o = \gamma \Delta t_s + \frac{\Delta l}{c}$$
$$\Delta l = \frac{v\gamma \Delta t_s}{c}$$
$$\frac{\Delta t_o}{\Delta t_s} = \frac{1 + v/c}{\sqrt{1- (v^2/c^2)}}$$
进一步简化后,我们得到:
$$1 + z = \sqrt{\frac{1+v/c}{1-v/c}}$$
上述表达式称为运动学多普勒频移表达式。
情况 4:运动观察者的相对论性情况
参考与情况 II 相同的图。由于相对论效应,观察到时间缩短,因此得到以下关系。(观察者以相对论速度运动)
$$\Delta t_o = \frac{\Delta t_s}{\gamma}+\frac{\Delta l}{c}$$
$$\Delta l = \frac{v\Delta t_o}{c}$$
$$\frac{\Delta t_o}{\Delta t_s} = \frac{\sqrt{1-( v^2/c^2)}}{1-v/c}$$
进一步简化后,我们得到:
$$1 + z = \sqrt{\frac{1+ v/c}{1- v/c}}$$
上述表达式与情况 III 得到的结果相同。
要点
恒星的退行速度和红移是相关的量。
在非相对论性情况下,我们无法确定光源是运动的还是静止的。
在相对论性情况下,对于运动的光源或观察者,红移与退行速度的关系没有区别。
运动的时钟走得慢,是相对论的直接结果。
红移与运动学多普勒频移
红移z = 10的星系对应于v≈80%的c。如果考虑暗物质,银河系的质量约为1011M⊙,则为1012M⊙。因此,我们的银河系非常巨大。如果它以 80% 的c运动,则不符合物体如何运动的普遍概念。
我们知道:
$$\frac{v_r}{c} = \frac{\lambda_{obs} - \lambda{rest}}{\lambda_{rest}}$$
对于z的小值:
$$z = \frac{v_r}{c} = \frac{\lambda_{obs}-\lambda_{rest}}{\lambda_{rest}}$$
在下图中,通量和波长之间的关系图中,在连续谱的顶部有发射线。根据H-α线信息,我们可以得出结论,大约z = 7。这意味着星系以 70% 的c运动。我们正在观察位移并将其解释为速度。我们应该摆脱这种概念,并以不同的方式看待z。想象一下空间是一个二维网格,它代表了宇宙,如下所示。

将黑星视为我们自己的银河系,将蓝星视为另一个星系。当我们记录来自这个星系的光时,我们看到光谱并找出它的红移,即星系正在远离。当光子发射时,它具有相对速度。
如果空间正在膨胀会怎样?
这是光子的瞬时红移。两个星系之间空间的累积红移将趋于大的红移。波长最终会改变。这是空间的膨胀,而不是星系的运动学运动。
下图显示,如果相互引力超过膨胀,那么它就不参与哈勃定律。

在运动学多普勒频移中,红移是在发射时诱导到光子中的。在宇宙红移中,每一步都会累积红移。在引力势中,光子将发生蓝移。当它从引力势中爬出来时,它会发生红移。
根据狭义相对论,两个彼此经过的物体之间的相对速度不能大于光速。我们所说的速度是宇宙膨胀的速度。对于较大的 z 值,红移是宇宙的,而不是相对于我们而言物体实际退行速度的有效测量。
宇宙原理
它源于宇宙的哥白尼学说。根据这个学说,宇宙是均匀且各向同性的。宇宙中没有首选方向和位置。
均匀性意味着无论你居住在宇宙的哪个部分,你都会看到宇宙在各个部分都是相同的。各向同性意味着无论你朝哪个方向看,你都会看到相同的结构。
均匀性的一个合适的例子是稻田。从各个部分看它都是均匀的,但是当风吹过时,它的方向会有变化,因此它不是各向同性的。考虑一块平地上的山,一个观察者站在山顶上。他会看到平地的各向同性,但它不是均匀的。如果在一个均匀的宇宙中,在一个点上是各向同性的,那么它在任何地方都是各向同性的。
已经进行了大规模的调查以绘制宇宙图。斯隆数字巡天就是这样一项调查,它不太关注赤纬,而关注赤经。回溯时间约为 20 亿年。每个像素对应于星系的位置,颜色对应于形态结构。绿色代表蓝色螺旋星系,而红色伪彩色表示大质量星系。
星系存在于宇宙网的细丝状结构中,星系之间存在空洞。
$\delta M/M \cong 1$,即质量分布的波动为 1,M 是给定立方体中存在的物质质量。在这种情况下,取体积为 50 Mpc 的立方体。
对于边长为 1000 Mpc 的立方体,$\delta M/M \cong 10^{−4}$。
量化均匀性的一种方法是取质量波动。在较小的尺度上,质量波动会更高。
为了量化各向同性,考虑宇宙微波背景辐射。宇宙在大角度尺度上几乎是各向同性的。
要点
两个彼此经过的物体之间的相对速度不能大于光速。
宇宙原理指出宇宙是均匀且各向同性的。
这种均匀性存在于非常大的角度尺度上,而不是较小的尺度上。
SDSS(斯隆数字巡天)是绘制夜空图的努力,验证了宇宙原理。
宇宙度规与膨胀
根据能量守恒定律和质量守恒定律,包括质量在内的总能量 (E=mc2) 在宇宙中任何过程的每一步都保持不变。宇宙的膨胀本身消耗能量,这可能是来自光子波长(宇宙红移)的拉伸、暗能量相互作用等等。
为了加快对超过26,000个星系的巡天速度,史蒂芬·A·谢克特曼(Stephen A. Shectman)设计了一种能够同时测量112个星系的仪器。在一个金属板上钻孔,这些孔对应于天空中星系的位置。光纤电缆将来自每个星系的光传输到智利拉斯坎帕纳斯山卡内基天文台(Carnegie Observatories)的2.5米杜邦望远镜上的光谱仪的独立通道。
为了达到最大效率,使用了被称为漂移扫描测光法(Drift-Scan Photometry)的专业技术,其中望远镜指向观测区域的起始点,然后关闭自动驱动。望远镜静止不动,天空则漂移过去。计算机以与地球自转相同的速率读取来自CCD探测器(CCD Detector)的信息,从而产生一个在恒定天球纬度上的长而连续的图像。测光工作总共花费了450小时。
存在不同形式的噪声,其数学模型取决于其特性。各种物理过程在大尺度上改变了宇宙的功率谱。由于量子涨落赋予的初始功率谱遵循频率的负三次方,这是一种三维的粉红噪声谱(Pink Noise Spectrum)。
度量
在宇宙学中,首先必须对空间进行定义。度量是描述空间中点的数学表达式。天空的观测是在球面几何中进行的;因此,将使用球坐标系。两个紧密间隔的点之间的距离由下式给出:
$$ds^2 = dr^2 + r^2d\theta^2 + r^2 sin^2\theta d\phi^2$$
下图显示了三维非膨胀欧几里得空间中的几何形状。
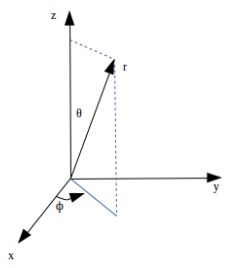
此几何形状仍然位于三维非膨胀欧几里得空间中。因此,定义框架本身的参考网格将是膨胀的。下图描绘了增大的度量。
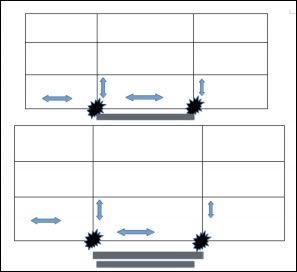
将一个比例因子放入非膨胀空间的方程中,称为“比例因子”,它包含了宇宙相对于时间的膨胀。
$$ds^2 = a^2(t)\left [ dr^2 + r^2d\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$$
其中a(t)是比例因子,有时写成R(t)。而a(t) > 1表示度量的放大,a(t) < 1表示度量的缩小,a(t) = 1表示度量恒定。按照惯例,a(t0) = 1。
共动坐标系
在共动坐标系(Comoving Coordinate System)中,测量尺度与框架(膨胀宇宙)一起膨胀。
这里,$\left [ dr^2 + r^2d\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$是共动距离,$ds^2$是固有距离。
固有距离将对应于在观测时刻测量的遥远星系到地球的实际距离,也就是物体的瞬时距离。
这是因为光子从遥远光源到达观测者时所经过的距离是在观测者的$t=t_0$时刻接收到的,这意味着瞬时观测距离将是固有距离,并且可以使用速率因子和初始测量长度作为参考来预测未来的距离。
共动距离和固有距离的概念对于测量观测空间给定体积内星系实际数密度值非常重要。必须使用共动距离来计算观测到的光子发射时星系的密度。一旦可以估计宇宙的膨胀速率,就可以获得这个值。
为了估计膨胀速率,可以观测长时间内观测到的遥远星系的距离变化。
要点
度量是描述空间中点的数学表达式。
比例因子决定宇宙是收缩还是膨胀。
在共动坐标系中,测量尺度与框架(膨胀宇宙)一起膨胀。
固有距离是物体的瞬时距离。
共动距离是物体的实际距离。
宇宙学 - 罗伯逊-沃克度量
在本章中,我们将详细了解罗伯逊-沃克度量。
随时间变化的比例因子的模型
假设一个光子从遥远的星系发出。空间对于光子来说在各个方向上都是向前的。宇宙的膨胀是在所有方向上进行的。让我们看看比例因子如何在以下步骤中随时间变化。
步骤1 - 对于静态宇宙,比例因子为1,即共动距离的值是物体之间的距离。
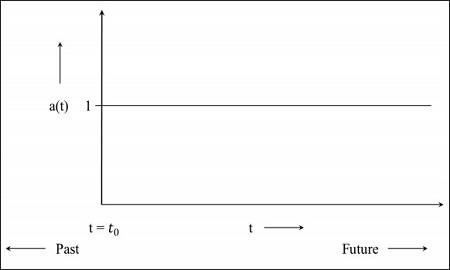
步骤2 - 下图是宇宙仍在膨胀但以减速率膨胀的图,这意味着该图将从过去开始。t = 0表示宇宙从那时开始。
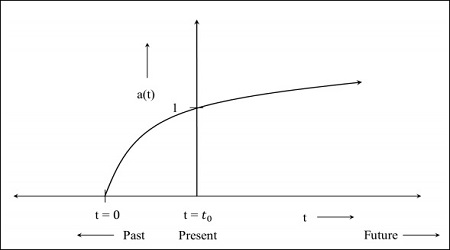
步骤3 - 下图是宇宙以更快速度膨胀的图。
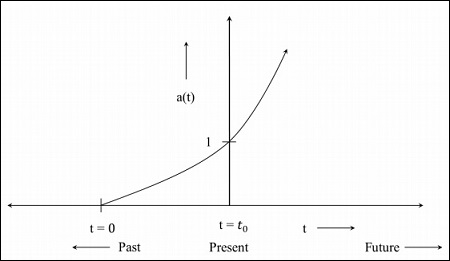
步骤4 - 下图是从现在开始收缩的宇宙图。
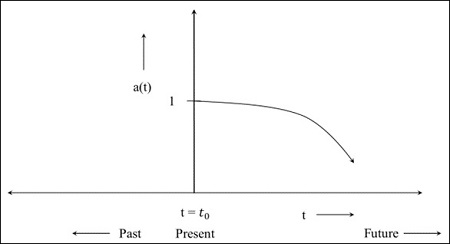
如果在宇宙收缩过程中比例因子的值变为0,则意味着物体之间的距离变为0,即固有距离变为0。共动距离是当前宇宙中物体之间的距离,是一个常数。未来,当比例因子变为0时,所有东西都会靠拢。该模型取决于宇宙的组成部分。
平坦(欧几里得:没有曲率参数)膨胀宇宙的度量表示为:
$$ds^2 = a^2(t)\left ( dr^2+r^2d\theta^2+r^2sin^2\theta d\varphi^2 \right )$$
对于时空,我们在上式中得到的线元素修改为:
$$ds^2 = c^2dt^2 - \left \{ a^2(t) \left ( dr^2 + r^2d\theta ^2 + r^2sin^2\theta d\varphi^2 \right ) \right \}$$
对于时空,光子发射和探测的时间是不同的。固有距离是物体的瞬时距离,由于宇宙的膨胀,它会随着时间而变化。它是光子从不同的物体传播到我们这里所经过的距离。它与共动距离的关系如下:
$$d_p = a(t) \times d_c$$
其中$d_p$是固有距离,$d_c$是共动距离,它是固定的。
在当前宇宙中测量的到物体的距离被认为是共动距离,这意味着共动距离是固定的,不会因膨胀而改变。在过去,比例因子小于1,这表明固有距离较小。
我们可以测量到星系的红移。因此,固有距离$d_p$对应于$c \times t(z)$,其中$t(z)$是朝向红移的回溯时间,c是真空中的光速。回溯时间是红移(z)的函数。
基于上述概念,让我们分析在这种$d_p = a(t) \times d_c$的情况下如何解释宇宙红移。
假设一个光子(地球上的)由星系G发射。$t_{em}$对应于光子发射的时间;$a(t_{em})$是光子发射时当时的比例因子。到光子被探测到时,整个宇宙已经膨胀了,即光子在探测时发生了红移。$t_{obs}$对应于光子被探测到的时间,相应的比例因子为$a(t_{obs})$。
宇宙增长因子由下式给出:
$$\frac{a(t_{obs})}{a(t_{em})}$$
波长膨胀因子为:
$$\frac{\lambda_{obs}}{\lambda_{em}}$$
它等于宇宙增长因子。符号具有其通常的含义。因此,
$$\frac{a(t_{obs})}{a(t_{em})} = \frac{\lambda_{obs}}{\lambda_{em}}$$
我们知道红移(z)为:
$$z=\frac{\lambda_{obs} - \lambda_{em}}{\lambda_{em}} = \frac{\lambda_{obs}}{\lambda_{em}} - 1$$
$$1 + z = \frac{a(t_{obs})}{a(t_{em})}$$
比例因子的当前值为1,因此$a(t_{obs}) = 1$,并将光子过去发射时的比例因子表示为$a(t)$。
因此,
$$1 + z = \frac{1}{a(t)}$$
宇宙学中红移的解释
为了理解这一点,让我们举个例子:如果$z = 2$,则$a(t) = 1/3$。
这意味着自从光离开那个物体以来,宇宙已经膨胀了三倍。接收到的辐射的波长膨胀了三倍,因为在其从发射物体传播的过程中,空间膨胀了相同的倍数。应该注意的是,对于如此大的z值,红移主要是宇宙红移,它不是物体相对于我们的实际退行速度的有效度量。
对于宇宙微波背景辐射(CMB),z = 1089,这意味着当前宇宙已经膨胀了∼1090倍。平坦、欧几里得、膨胀宇宙的度量表示为:
$$ds^2 = a^2(t)(dr^2 + r^2d\theta^2 + r^2sin^2\theta d\varphi^2)$$
我们希望将度量写入任何曲率。
罗伯逊和沃克证明了对于任何曲率宇宙(它是均匀且各向同性的),度量表示为:
$$ds^2 = a^2(t) \left [ \frac{dr^2}{1-kr^2} + r^2d\theta^2 + r^2sin^2\theta d\varphi^2 \right ]$$
这通常被称为罗伯逊-沃克度量(Robertson–Walker Metric),适用于任何空间拓扑。请注意$dr^2$中的额外因子。这里的𝑘是曲率常数。
宇宙的几何形状
宇宙的几何形状借助以下曲率来解释,其中包括:
- 正曲率
- 负曲率
- 零曲率
让我们详细了解每一个。
正曲率
如果在曲率曲面上任意一点绘制的切平面不与曲面上的任何点相交,则该曲面称为正曲率曲面,即曲面始终位于该点的切平面的同一侧。球面具有正曲率。
负曲率
如果在曲率曲面上某一点绘制的切平面与曲面上的任何点相交,则该曲面称为负曲率曲面,即曲面在两个不同的方向上远离切平面弯曲。马鞍形曲面具有负曲率。
现在考虑球面。如果通过连接三个点用测地线(大圆弧)在球面上构造一个三角形,则球面三角形的内角和大于 180o,即 −
$$\alpha + \beta + \gamma > \pi$$
这样的空间称为正曲率空间。此外,曲率是均匀且各向同性的。一般来说,球面三角形顶点的角度遵循以下关系 −
$$\alpha + \beta +\gamma = \pi + A/R^2$$
其中A是三角形的面积,R是球体的半径。下图描绘了一个正曲率空间。
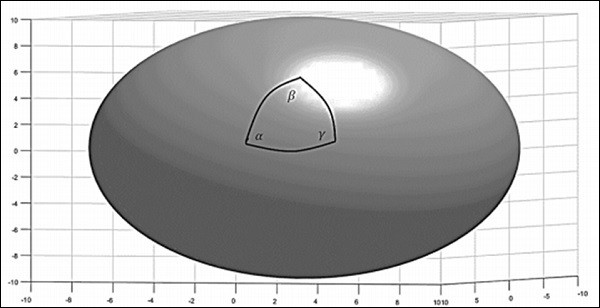
对于正曲率,平行线应该相交。考虑地球表面,它是一个正曲率空间。在地球赤道上取两个起点。垂直于赤道穿过赤道的线被称为经线。由于这些线垂直于赤道相交,因此可以将它们称为平行线。从赤道开始,它们最终在两极相交。这种方法被卡尔·高斯等人用来理解地球的拓扑结构。
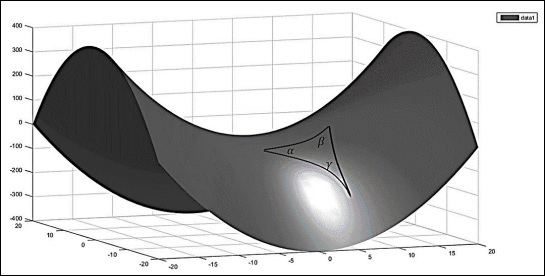
考虑一个负曲率空间(下图所示的马鞍),三角形的内角和小于 180o,即 −
$$\alpha + \beta + \gamma < \pi$$
顶点的角度遵循以下关系 −
$$\alpha + \beta + \gamma = \pi - A/R^2$$
零曲率
平面曲面具有零曲率。现在对于一个平面空间,如果取一个平面并通过用测地线(直线)连接三个点来构造一个三角形,则内角和将为 −
$$\alpha + \beta + \gamma = \pi$$
下图是一个平坦的二维空间。
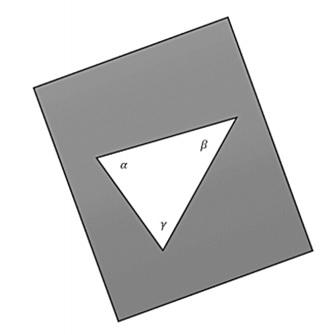
如果想要一个均匀且各向同性的空间,则只剩下三种可能性:空间可以是均匀平坦的,也可以具有均匀的正曲率,或者可以具有均匀的负曲率。
曲率常数可以取以下三个值中的任何一个。
$$k = \begin{cases}+1, & 正曲率空间;\\\quad 0, & 平坦空间; \\-1, & 负曲率空间;\end{cases}$$
宇宙的全局拓扑结构
宇宙具有一定的拓扑结构,但在局部可能存在褶皱。根据物质在空间中的分布情况,曲率存在较小的变化。让我们假设有一类物体,无论它位于宇宙中的哪个位置,其真实大小都相同,这意味着它们就像标准烛光一样。它们的亮度不同,但大小相同。
如果物体位于正曲率空间中,并且光子来自点 A(物体的一端)和点 B(物体的另一端),则光子将在正曲率空间中沿测地线路径平行传播,并最终相遇。对于 C 点的观察者来说,它似乎来自不同方向的两个不同点。
如果物体位于局部宇宙中,我们测量角大小,它不受曲率的影响。如果在更大的红移处看到同一类物体,则角大小与之不相关。
$$\theta = \frac{d}{r}$$
其中d是物体的尺寸,r是到物体的距离,即如果尺寸大于局部尺寸,则意味着曲率为正。下图是正曲率空间中检测到的光子的表示。
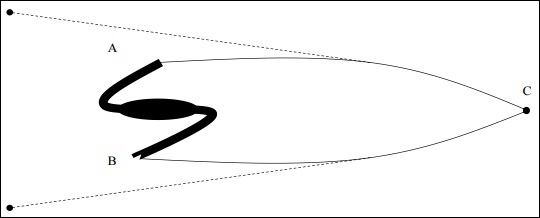
需要注意的是,没有真正具有标准尺寸和形态的天体物理物体。虽然人们认为巨大的椭圆cD星系符合标准烛光的标准,但后来发现它们也随时间演化。
寻找星系的距离
在本节中,我们将讨论如何通过考虑下图来找到星系的距离。
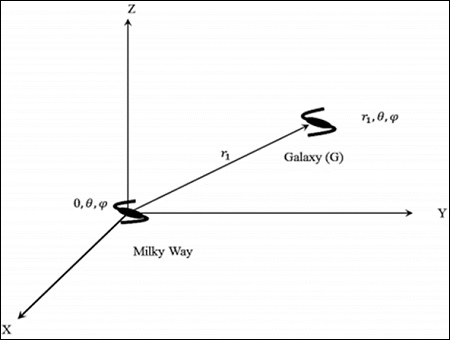
在宇宙静止参考系中考虑位于 (r, θ,) 的银河系。可以通过调用均匀性假设来取 𝑟 = 0; (0, θ,ϕ),即宇宙的中心。
考虑位于 (r1, θ,) 的星系“G”。距离(固有距离)是光子传播的最短径向距离。根据时空的对称性,从 r = 0 到 r = r1 的零测地线在空间中具有恒定的方向。在其径向传播中,角度坐标不会改变。如果角度坐标发生改变,则它不是最短路径。这就是为什么曲率项存在于 dr2 中的原因。
要点
宇宙的膨胀是向所有方向的。
宇宙可以是静态的、膨胀的或收缩的,这取决于比例因子的演化。
cD星系会随时间演化,因此不能用作标准烛光。
宇宙具有一定的拓扑结构,但在局部可能存在褶皱。
哈勃参数与比例因子
本章将讨论哈勃参数和比例因子。
先决条件 − 宇宙红移,宇宙原理。
假设 − 宇宙是均匀且各向同性的。
哈勃常数与比例因子变化率的关系
在本节中,我们将哈勃常数与比例因子变化率联系起来。
我们可以用以下方式写出速度并简化。
$$v = \frac{\mathrm{d} r_p}{\mathrm{d} t}$$
$$= \frac{d[a(t)r_c}{dt}$$
$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast (ar_c)$$
$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast r_p$$
这里,v是退行速度,a是比例因子,rp是星系之间的固有距离。
哈勃经验公式的形式为 −
$$v = H \ast r_p$$
因此,比较上述两个方程,我们得到 −
哈勃参数 = 比例因子的变化率
$$H = da/dt \ast 1/a$$
注意 − 这不是一个常数,因为比例因子是时间的函数。因此它被称为哈勃参数,而不是哈勃常数。
经验上我们写 −
$$H = V/D$$
因此,从这个方程中,我们可以推断,由于D在增加而V是一个常数,那么H随着时间的推移和宇宙的膨胀而减小。
弗里德曼方程与罗伯逊-沃克模型结合
在本节中,我们将了解弗里德曼方程如何与罗伯逊-沃克模型结合使用。为了理解这一点,让我们以以下图像为例,该图像中有一个距离为rp的试验质量与质量为M的天体。
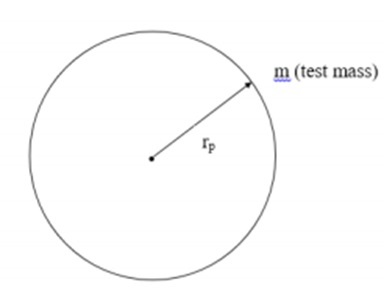
考虑到上图,我们可以将力表示为 −
$$F = G \ast M \ast \frac{m}{r^2_p}$$
这里,G是万有引力常数,ρ是可观测宇宙内的物质密度。
现在,假设球体内质量密度均匀,我们可以写 −
$$M = \frac{4}{3} \ast \pi \ast r_p^3 \ast \rho$$
将这些代回到我们的力方程中,我们得到 −
$$F = \frac{4}{3} \ast \pi \ast G \ast r_p \ast \rho \ast m$$
因此,我们可以将质量m的势能和动能写为 −
$$V = -\frac{4}{3} \ast \pi \ast G \ast r^2_p \ast m \ast \rho$$
$$K.E = \frac{1}{2} \ast m \ast \frac{\mathrm{d} r_p^2}{\mathrm{d} t}$$
使用维里定理 −
$$U = K.E + V$$
$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} r_p}{\mathrm{d} t} \right )^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$
但是这里,$r_p = ar_c$。所以我们得到 −
$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} a}{\mathrm{d} t} \right )^2 r_c^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$
进一步简化后,我们得到弗里德曼方程,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi}{3} \ast G \ast \rho + \frac{2U}{m} \ast r_c^2 \ast a^2$$
这里U是一个常数。我们还注意到,我们目前生活的宇宙是由物质主导的,而辐射能量密度非常低。
要点
哈勃参数随着时间的推移和宇宙的膨胀而减小。
我们目前生活的宇宙是由物质主导的,辐射能量密度非常低。
弗里德曼方程与宇宙模型
本章将了解弗里德曼方程是什么,并详细研究不同曲率常数的世界模型。
弗里德曼方程
该方程告诉我们关于宇宙均匀且各向同性模型中空间膨胀的信息。
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho + \frac{2U}{mr_c^2a^2}$$
这在广义相对论(GR)和罗伯逊-沃克度规的背景下进行了修改,如下所示。
使用 GR 方程 −
$$\frac{2U}{mr_c^2} = -kc^2$$
其中k是曲率常数。因此,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8 \pi G}{3}\rho - \frac{kc^2}{a^2}$$
此外,ρ被能量密度取代,其中包括物质、辐射和任何其他形式的能量。但出于表示目的,它写成ρ。
不同曲率常数的世界模型
现在让我们根据曲率常数值查看各种可能性。
情况 1:k=1,或封闭宇宙
对于膨胀宇宙,$da/dt > 0$。随着膨胀继续,上述方程右侧的第一项为 $a^{-3}$,而第二项为 $a^{-2}$。当这两项相等时,宇宙停止膨胀。然后 −
$$\frac{8 \pi G}{3}\rho = \frac{kc^2}{a^2}$$
这里,k=1,因此,
$$a = \left [ \frac{3c^2}{8 \pi G\rho} \right ]^{\frac{1}{2}}$$
这样的宇宙是有限的,并且体积有限。这被称为封闭宇宙。
情况 2:k=-1,或开放宇宙
如果k < 0,膨胀将永远不会停止。在某个时刻,与第二项相比,可以忽略右侧的第一项。
这里,k = -1。因此,$da/dt ∼ c$。
在这种情况下,宇宙正在匀速运动。这样的宇宙具有无限的空间和时间。这被称为开放宇宙。
情况 3:k=0,或平坦宇宙
在这种情况下,宇宙以减小的速度膨胀。这里,k = 0。因此,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho$$
这样的宇宙具有无限的空间和时间。这被称为平坦宇宙。
要点
弗里德曼方程告诉我们关于宇宙均匀且各向同性模型中空间膨胀的信息。
根据不同的曲率常数值,我们可以拥有封闭宇宙、开放宇宙或平坦宇宙。
宇宙学 - 流体方程
本章将讨论流体方程以及它如何告诉我们宇宙的密度随时间变化。
估计当前宇宙中的ρc和ρ
对于当前宇宙 −
$$\rho_c \simeq 10^{11}M_\odot M_{pc}^{-3} \simeq 10\: 氢原子 \: m^{-3}$$
宇宙空间存在着各种各样的临界密度。例如,星系际介质的临界密度ρc为每立方米1个氢原子,而分子云的临界密度则为每立方米10⁶个氢原子。
我们必须考虑适当的空间样本测量ρc。在我们的星系内,ρc的值非常高,但我们的星系并不能代表整个宇宙。因此,我们应该到宇宙学原理成立的宇宙空间中去,即距离≈300 Mpc。观察300 Mpc意味着回溯10亿年前,但这仍然是现在的宇宙。
像SDSS这样的巡天调查被用来确定实际的物质密度。它们选取一个5×500×5 Mpc³的体积,计算星系数量,并累加来自这些星系的所有光线。假设1 L ≡ 1 M,即1个太阳光度≡1个太阳质量。
我们进行光到质量的转换,然后尝试根据该体积中存在的可见物质粒子来估计重子数。
例如:
$$1000L_\odot ≡ 1000M_\odot / m_p$$
其中,mp=质子质量。
然后我们得到大约的重子数密度Ωb ≈ 0.025。这意味着ρb = ρc的0.25%。不同的调查结果略有不同。因此,在局部宇宙中,可见物质的数密度远小于临界密度,这意味着我们生活在一个开放的宇宙中。
这些调查没有包含质量因数为10的物质,因为这些调查考虑的是电磁辐射,而不是暗物质。因此,Ωm = 0.3 - 0.4。这仍然得出我们生活在一个开放宇宙中的结论。
暗物质与引力相互作用。大量的暗物质可以阻止宇宙膨胀。我们还没有确定ρ如何随时间变化,这需要另一组方程。
热力学指出:
$$dQ = dU + dW$$
对于一个体积增长的系统,dW = P dV。宇宙的膨胀被建模为绝热的,即dQ = 0。因此,体积变化应该来自内能的变化dU。
让我们取一定体积的宇宙,其共动半径为单位,即rc = 1。如果ρ是该空间体积内物质的密度,则:
$$M = \frac{4}{3} \pi a^3r_c^3 \rho$$
$$U = \frac{4}{3}\pi a^3\rho c^2$$
其中,**U**是能量密度。让我们找出宇宙膨胀时内能随时间的变化。
$$\frac{\mathrm{d} U}{\mathrm{d} t} = 4 \pi a^2 \rho c^2 \frac{\mathrm{d} a}{\mathrm{d} t} + \frac{4}{3}\pi a^3 c^2\frac{\mathrm{d} \rho}{\mathrm{d} t}$$
同样,体积随时间的变化由下式给出:
$$\frac{\mathrm{d} V}{\mathrm{d} t} = 4\pi a^2 \frac{\mathrm{d} a}{\mathrm{d} t}$$
代入dU = −P dV。我们得到:
$$4\pi a^2(c^2 \rho +P)\dot{a}+\frac{4}{3}\pi a^3c^2\dot{\rho} = 0$$
$$\dot{\rho}+3\frac{\dot{a}}{a}\left ( \rho + \frac{P}{c^2} \right ) = 0$$
这被称为**流体方程**。它告诉我们宇宙的密度如何随时间变化。
宇宙膨胀时压力下降。在每一时刻压力都在变化,但在所考虑的体积内两点之间没有压力差,因此压力梯度为零。只有相对论物质才会产生压力,物质本身没有压力。
弗里德曼方程与流体方程一起模拟宇宙。
要点
暗物质与引力相互作用。大量的暗物质可以阻止宇宙膨胀。
流体方程告诉我们宇宙的密度如何随时间变化。
弗里德曼方程与流体方程一起模拟宇宙。
只有相对论物质才会产生压力,物质本身没有压力。
宇宙学 - 物质主导宇宙
在本章中,我们将讨论与物质主导宇宙相关的弗里德曼方程的解。在宇宙学中,因为我们在大尺度上观察一切,太阳系、星系,所有的一切都像尘埃粒子一样(这就是我们用肉眼看到的样子),我们可以称之为尘埃宇宙或仅物质宇宙。
在**流体方程**中:
$$\dot{\rho} = -3\left ( \frac{\dot{a}}{a} \right )\rho -3\left ( \frac{\dot{a}}{a} \right )\left ( \frac{P}{c^2} \right )$$
我们可以看到存在一个压力项。对于尘埃宇宙,**P = 0**,因为物质的能量密度将大于辐射压力,并且物质没有以相对论速度运动。
因此,流体方程将变为:
$$\dot{\rho} = -3\left ( \frac{\dot{a}}{a} \right )\rho$$
$$\Rightarrow \dot{\rho}a + 3\dot{a}\rho = 0$$
$$\Rightarrow \frac{1}{a^3}\frac{\mathrm{d}}{\mathrm{d} t}(a^3 \rho) = 0$$
$$\Rightarrow \rho a^3 =\: 常数$$
$$\Rightarrow \rho \propto \frac{1}{a^3}$$
这个方程没有违反直觉,因为密度应该按a⁻³缩放,因为体积随a³增加。
从最后一个关系,我们可以说:
$$\frac{\rho (t)}{\rho_0} = \left [ \frac{a_0}{a(t)} \right ]^3$$
对于现在的宇宙,a等于a₀,应该为1。因此:
$$\rho(t) = \frac{\rho_0}{a^3}$$
在物质主导的平坦宇宙中,k = 0。因此,弗里德曼方程将变为:
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8 \pi G\rho}{3}$$
$$\dot{a}^2 = \frac{8\pi G \rho a^2}{3}$$
通过求解这个方程,我们将得到:
$$a \propto t^{2/3}$$
$$\frac{a(t)}{a_0} = \left ( \frac{t}{t_0} \right )^{2/3}$$
$$a(t) = \left( \frac{t}{t_0} \right )^{2/3}$$
这意味着宇宙将以减小的速度持续膨胀。下图显示了尘埃宇宙的膨胀。
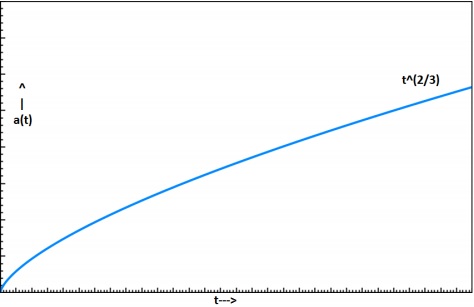
ρ如何随时间变化?
看看下面的方程:
$$\frac{\rho(t)}{\rho_0} = \left ( \frac{t_0}{t} \right )^2$$
我们知道比例因子随时间变化为t²/³。因此:
$$a(t) = \left ( \frac{t}{t_0} \right )^{2/3}$$
对其求导,我们将得到:
$$\frac{(da)}{dt} = \dot{a} = \frac{2}{3} \left ( \frac{t^{-1/3}}{t_0} \right )$$
我们知道**哈勃常数**是:
$$H(t) = \frac{\dot{a}}{a} = \frac{2}{3t}$$
这是**爱因斯坦-德西特宇宙**的方程。如果我们想计算宇宙的当前年龄,那么:
$$t_0 = t_{年龄} = \frac{2}{3H_0}$$
代入当前宇宙的H₀值后,我们将得到宇宙年龄的值为**90亿年**。在我们自己的银河系中,有很多**球状星团**的年龄超过这个值。
这就是关于尘埃宇宙的全部内容。现在,如果您假设宇宙是由辐射而不是物质主导的,那么辐射能量密度将随a⁻⁴变化,而不是a⁻³。我们将在下一章中详细讨论。
要点
在宇宙学中,所有的一切都像尘埃粒子一样,因此,我们称之为尘埃宇宙或仅物质宇宙。
如果我们假设宇宙是由辐射而不是物质主导的,那么辐射能量密度将随a⁻⁴变化,而不是a⁻³。
宇宙学 - 辐射主导宇宙
在本章中,我们将讨论与辐射主导宇宙相关的弗里德曼方程的解。首先,我们将比较物质的能量密度与辐射的能量密度。这将使我们能够判断我们的宇宙是物质主导的还是辐射主导的。
辐射能量密度
当前宇宙中普遍存在的辐射很少归因于恒星源,但主要归因于残余的CMB(宇宙微波背景)。
辐射的能量密度εγ,0可以表示如下:
$$\epsilon_{\gamma,0} = aT_0^4$$
这里,**a**是辐射常数,其表达式为(8π⁵kB⁴)/(15h³c²) 等于 **a = 7.5657 × 10⁻¹⁵ erg cm⁻³ K⁻⁴**。我们在这里考虑的温度T₀对应于CMB的黑体温度。
代入结果,我们有:
$$\epsilon_{\gamma,0} = aT_0^4 = 4 \times 10^{-13}erg\: cm^{-3}$$
物质能量密度
在下述计算中,我们假设使用平坦宇宙且K = 0。我们将物质的能量密度考虑为ε = ρc²。我们考虑以下内容:
$$\rho_{m,0}c^2 = 0.3\rho_{c,0}c^2 = 0.3 \times \frac{3H_0^2}{8\pi G} \times c^2$$
$$\rho_{m,0}c^2 \simeq 2 \times 10^{-8} erg \:cm^{-3}$$
$$\rho_{b,0}c^2 = 0.03\rho_{c,0}c^2 = 0.03 \times \frac{3H_0^2}{8\pi G} \times c^2$$
$$\rho_{b,0}c^2 \simeq 2 \times 10^{-9} erg\: cm^{-3}$$
因此,从上述计算中,我们看到我们生活在一个物质主导的宇宙中。这可以从CMB非常冷的事实得到支持。当我们回溯时间时,CMB温度会变得越来越热,并且能够得出结论,可能存在一个宇宙由辐射主导的时期。
密度和比例因子的变化
流体方程向我们展示了:
$$\dot{\rho} + 3\frac{\dot{a}}{a}\left ( \rho + \frac{P}{c^2} \right ) = 0$$
如果我们考虑尘埃宇宙,我们将有P = 0。撇开之前的结果,我们将宇宙视为由辐射主导的。
$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{P}{c^2} \right ) = 0$$
使用压力关系Prad = ρc²/3,我们有:
$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{\rho_{rad}}{3} \right ) = 0$$
$$\dot{\rho}_{rad} + 4\frac{\dot{a}}{a}(\rho_{rad}) = 0$$
进一步简化,我们有:
$$\frac{1}{a^4}\frac{\mathrm{d}}{\mathrm{d} t}(\rho_{rad}a^4) = 0$$
$$\rho_{rad}a^4 =\: 常数$$
$$\rho_{rad} \propto \frac{1}{a^4}$$
上述结果显示a与ρ的-4次方反比变化。
这可以在物理上解释为体积变化带来的a⁻³。剩余的a⁻¹可以被视为由于宇宙空间膨胀而导致光子损失的能量(宇宙红移1 + z = a⁻¹)。
下图显示了物质和辐射密度随时间的变化。
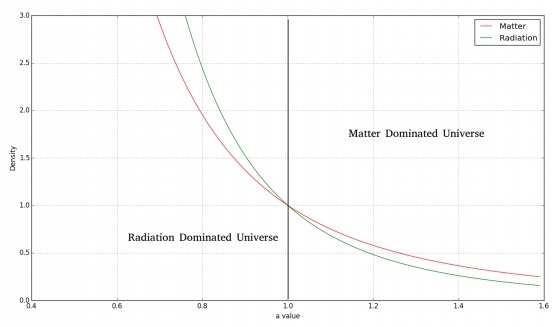
对于平坦的辐射主导宇宙,弗里德曼方程如下:
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G\rho}{3}$$
$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\frac{\rho_0}{a^4}$$
简化并应用微分方程的解,我们有:
$$(\dot{a})^2 = \frac{8\pi G\rho_0}{3a^2}$$
$$\Rightarrow a(t) \propto t^{\frac{1}{2}}$$
因此,我们有:
$$a(t) = a_0 \left ( \frac{t}{t_0} \right )^{\frac{1}{2}}$$
从上述方程,我们看到比例因子的增长率小于尘埃宇宙。
要点
当前宇宙中普遍存在的辐射很少归因于恒星源。
对于尘埃宇宙,压力为零。
CMB非常冷。
宇宙学 - 暗能量
暗能量领域在天文学中是一个非常模糊的领域,因为它在所有方程中都是一个自由参数,但对其究竟是什么并没有明确的概念。
我们将从弗里德曼方程开始:
$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2}$$
大多数关于宇宙学的入门书籍,它们都从哈勃观测之前的宇宙是封闭且静止的这一事件开始描述暗能量。
为了使宇宙在右侧保持静态,这两个项必须相等且都为零。但如果第一项大于第二项,宇宙将不会是静态的。因此,爱因斯坦在场的方程中引入了自由参数∧来使宇宙静态。他认为,无论第一项与第二项相比如何,只要方程中多出一个分量来补偿这两个项之间的差异,就能始终得到一个静态的宇宙。
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2} + \frac{\wedge}{3}$$
$$\left ( \frac{\ddot{a}}{a} \right ) = -\frac{4 \pi G}{3}\left ( \rho + \frac{3P}{c^2} \right ) + \frac{\wedge}{3}$$
其中 $P = \rho \ast c^2/3$ 且 $\wedge = \rho \ast c^2$ 是宇宙学常数。(负号仅因万有引力吸引作用)
在上式(加速度方程)中:
$3P/c^2$ 是由于辐射引起的负压,
$-4\pi G/3$ 是由于万有引力引起的吸引力,
$\wedge/3$ 作出正贡献。
第三项起斥力的作用,因为方程的另一部分是吸引力。
该方程的物理意义在于˙a = 0,因为当时没有任何证据表明宇宙正在膨胀。如果这两个项不匹配,那么最好添加一个分量,并根据偏移量来改变自由参数的值。
当时对这个宇宙学常数没有物理学解释,这就是为什么当宇宙膨胀的解释在20世纪20年代被发现时,爱因斯坦不得不立即抛弃这个常数的原因。
这个宇宙学常数的解释仍在使用,因为它解释了宇宙的不同版本,但这个宇宙学常数的定义和解释方式随着时间的推移而不断变化。
现在,由于许多原因,宇宙学常数的概念又被带回了宇宙学。其中一个原因是,我们对宇宙不同成分(重子物质、暗物质、辐射)的能量密度有了观测数据,所以我们知道这个参数是什么。利用宇宙微波背景辐射的独立观测表明 k=0。
$$CMB, k=0\: \rho = \rho_c = \frac{3H_0^2}{8\pi G} \approx 10 \: 氢原子.m^{-3}$$
为了使 k 为 0,ρ 应该等于 ρc,但我们知道,如果将所有已知成分加起来,结果不等于 0,这意味着存在某种其他成分,其值远小于 ρc。
$$\rho = \rho_b + \rho_{DM} + \rho_{rad} << \rho_c$$
暗能量的另一个证据来自Ia型超新星观测,Ia型超新星发生在白矮星吸积物质并超过钱德拉塞卡极限(≈ 1.4M)时。每次Ia型超新星爆发时,其质量都相同,这意味着系统的总结合能相同,我们能够看到的可见光能量也相同。
当然,超新星的光度会先增强然后减弱,但如果你测量峰值亮度,它总是相同的,这使其成为一个标准的候选者。因此,利用Ia型超新星,我们可以测量宇宙的宇宙学分量,天文学家发现,高红移的超新星比低红移的超新星暗 30%−40%,如果存在非零的∧项,就可以解释这种现象。
在宇宙学模型中,DE(暗能量)被视为一种流体,这意味着我们可以写出它的状态方程。状态方程是连接物质两种不同状态的变量(如压力、密度、温度和体积)的方程。
从量纲上看,
$$\frac{8 \pi G}{3}\rho = \frac{\wedge}{3}$$
$$\rho_\wedge = \frac{\wedge}{8\pi G}$$
暗能量的能量密度为:
$$\epsilon_\wedge = \rho_\wedge \ast c^2 = \frac{\wedge c^2}{8 \pi G}$$
暗能量密度参数为:
$$\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$$
Ω∧是暗能量密度与临界密度之比。
$$\rho = \rho_b + \rho_{DM} +\rho_\wedge$$
关于暗能量有很多理论,暗能量正在排斥宇宙并导致宇宙膨胀。一个假设是,暗能量可能是真空能量密度。假设空间本身正在产生某种能量,当你计算空间单位体积内重子物质、暗物质和辐射的能量时,你也在计算与空间相关的能量,但这并不清楚暗能量是否真的是真空能量密度。
我们知道暗物质和辐射的密度与比例因子之间的关系是:
$$\rho_m \propto \frac{1}{a^3}$$
$$\rho_m \propto \frac{1}{a^4}$$
我们有密度与比例因子的关系图。在同一图中,我们可以看到ρ∧随着宇宙膨胀是一个常数,不依赖于比例因子。
下图显示了密度和比例因子之间的关系。
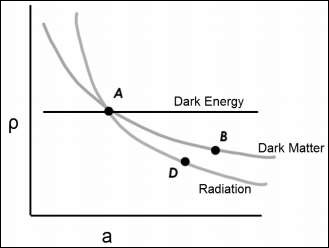
‘ρ’ 与 ‘a’(比例因子与时间有关)在同一图中,暗能量被建模为常数。因此,无论我们在当前宇宙中测量到多少暗能量,它都是一个常数。
要点
利用宇宙微波背景辐射的独立观测表明 k=0。
ρ∧随着宇宙膨胀是一个常数,不依赖于比例因子。
引力也随时间变化,这被称为修正牛顿动力学。
宇宙学 - 螺旋星系旋转曲线
本章将讨论螺旋星系旋转曲线以及暗物质的证据。
暗物质和关于暗物质的观测事实
暗物质的早期证据是对螺旋星系运动学的研究所得。
太阳距我们银河系的中心偏移了3万光年。银心速度为220公里/秒。
为什么速度是220公里/秒而不是100公里/秒或500公里/秒?是什么控制着天体的圆周运动?
半径内包含的质量有助于探测宇宙中的速度。
银河系或螺旋星系的旋转 - 微分旋转
角速度随距中心的距离而变化。
轨道周期取决于距中心的距离。
靠近银河系中心的物质周期较短,远离银河系中心的物质周期较长。
旋转曲线
预测速度随银心半径的变化。该曲线给出了速度随轨道半径的变化。
当我们看到物体运动时,我们认为是引力影响了旋转。
质量分布随半径而变化。物质密度将预测旋转曲线。基于随半径变化的物质密度的旋转曲线。
表面亮度
我们选择一个区域,看看有多少光发出。
从该区域发出的光量称为表面亮度。
其单位为mag/arcsec2。
如果我们发现表面亮度随半径变化,我们可以发现发光物质随半径变化。
$$\mu(r) \propto exp \left( \frac{-r}{h_R} \right )$$
$h_R$ 是尺度长度。$\mu(r) = \mu_o \ast exp \left( \frac{-r}{h_R} \right )$
$h_R$ 对于银河系来说大约是 3 kpc。
螺旋星系
为了理解旋转曲线,天文学家将星系分成两个部分:
- 盘
- 核球
下图显示了一个中心球形核球+圆盘。核球和盘中的恒星和气体分布不同。
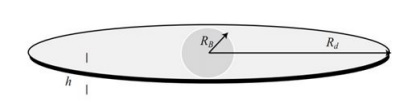
螺旋星系的运动学
-
任何物体的圆周速度 - 对于核球 (r < Rb)。
$$V^2(r) = G \ast \frac{M(r)}{r}$$
$$M(r) = \frac{4\pi r^3}{3} \ast \rho_b$$
-
对于盘 - (Rb < r < Rd)
$$V^2(r) = G \ast \frac{M(r)}{r}$$
核球具有大致恒定的恒星密度。
核球内的密度是恒定的(在核球内的距离不随距离变化)。
在盘中,恒星密度随半径减小。半径增加,发光物质减少。
在核球中 - $V(r) \propto r$
在盘中 - $V(r) \propto 1/\sqrt{r}$
螺旋星系的旋转曲线
通过光谱学(附近的星系 - 空间分辨星系),我们绘制了旋转曲线。
如上所述,我们看到旋转曲线在外区是平坦的,即外区物体运动速度很快,这通常不是这种形式。
轨道速度随着内区半径的增加而增加,但在外区变平。
暗物质
暗物质被认为是宇宙的非发光成分。让我们通过以下几点来了解暗物质。
平坦的旋转曲线与我们在螺旋星系中看到的恒星和气体分布相反。
盘的表面光度随半径呈指数下降,这意味着发光物质(主要是恒星)的质量集中在银河系中心附近。
旋转曲线的平坦化表明,在一定半径r内星系的总质量总是随着r的增加而增加。
这只有在这些星系中存在大量看不见的具有引力的物质,并且不发出电磁辐射的情况下才能解释。
螺旋星系的旋转曲线测量是暗物质最令人信服的证据之一。
暗物质的证据
缺失质量 - 发光质量的 10 倍。
大部分暗物质必须位于星系的晕中:盘中大量暗物质会扰乱盘对抗潮汐力的长期稳定性。
盘中一小部分暗物质可能是重子物质 - 暗淡的恒星(褐矮星、黑矮星)和致密的恒星残余物(中子星、黑洞)。但这种重子暗物质无法解释星系中缺失质量的全部规模。
暗物质的密度剖面 - $M(r) \propto r$ 和 $\rho(r) \propto r^{−2}$。
螺旋星系的旋转曲线数据与分布在其晕中的暗物质一致。
这个暗晕构成了星系大部分的总质量。
所有重子物质(恒星、星团、星际介质等)都由这个暗物质晕的引力势束缚在一起。
结论
暗物质只通过其与普通物质的引力相互作用被探测到。尚未观测到其与光(无电磁力)的相互作用。
中微子——无电荷,弱相互作用,但质量太小(< 0.23 eV)。为了解释结构的形成,暗物质粒子应该具有 E > 10 eV 左右的能量。
弱相互作用大质量粒子 (WIMP) 可能是暗物质的来源。
要点
靠近银河系中心处的物质具有较短的周期。
核球具有大致恒定的恒星密度。
星盘的表面光度随半径呈指数下降。
星盘中大量的暗物质可能会扰乱星盘抵抗潮汐力的长期稳定性。
星系速度弥散测量
暗物质的第一个直接证据来自弗里茨·兹威基 (Fritz Zwicky)。他进行了一些观测,首次揭示了暗物质的存在。他的观测考虑了星系团内的整体运动。
扩展的天体是星系团,它们被认为是束缚结构。这些星系相对于星系团中心运动,但不会飞散出去。我们观察星系的整体运动。
假设:速度代表潜在的潜在能量
每个星系在星系团内都有其自身的自行运动和哈勃流分量。较小的星系较小,大部分光来自M31和银河系,还有几个矮星系。对于我们的粗略分析,我们只能使用M31和银河系来评估本星系群的动力学质量。
我们和M31之间存在相对速度。这很粗略,但它是真实的。故事开始很久以前,那时M31和银河系彼此靠近,因为它们都是一个星系团的成员,它们彼此远离。一段时间后,它们达到最大分离距离,然后彼此靠近。
让我们假设它们所能达到的最大分离距离为$r_{max}$。现在它们的分离距离称为r。设M为M31和银河系的总质量。我们不知道$r_{max}$何时达到。
$$ \frac{GM}{r_{max}} = 在r_{max}处的势能 $$
当这些星系在某一时刻r彼此靠近时,系统的能量将为:
$$ \frac{1}{2}\sigma^2 = \frac{GM}{r} = \frac{GM}{r_{max}} $$
σ是两个星系的相对速度。M只是约化质量,但检验质量为1。σ是距离星团中心r处任何物体的速度。我们相信这个星团处于动态平衡状态,因为维里定理成立。因此,星系不能以不同的速度运动。
这些星系需要多长时间才能达到最大距离?
为了理解这一点,让我们考虑以下方程:
$$ \frac{1}{2}\left ( \frac{dr}{dt} \right )^2 = \frac{GM}{r} - \frac{GM}{r_{max}} $$
$$ t_{max} = \int_{0}^{r_{max}} dt = \int_{0}^{r_{max}} \frac{dr}{\sqrt{2GM}}\left ( \frac{1}{r} - \frac{1}{r_{max}} \right )^2 $$
$$ t_{max} = \frac{\pi r_{max}^{\frac{3}{2}}}{2\sqrt{2GM}} $$
其中,M = 本星系群的动力学质量。从碰撞开始到结束的总时间为$2t_{max}$。因此,
$$ 2t_{max} = t_0 + \frac{D}{\sigma} $$
而$t_0$是宇宙的当前年龄。
如果实际的$t_{max} < 右侧值$,那么我们就有时间的下限。$D/\sigma$是它们再次碰撞的时间。这里,我们假设σ是常数。
$$ t_{max} = \frac{t_0}{2} + \frac{D}{2\sigma} $$
$$ r_{max} = t_{max} \times \sigma = 770K_{pc} $$
这里,σ = 银河系和M31之间的相对速度。
$$ M_{dynamic} = 3 \times 10^{12}M_0 $$
$$ M_{MW}^{lum} = 3 \times 10^{10}M_0 $$
$$ M_{M31}^{lum} = 3 \times 10^{10}M_0 $$
但实际上,动力学质量是考虑星系团内每个星系计算出来的。缺失的质量就是暗物质,而弗里茨·兹威基 (Fritz Zwicky)注意到后发座星系团中的星系运动速度太快。他预测了中子星存在的可能性,仅仅在中子星被发现的第二年,他利用帕洛玛天文台寻找超新星。
要点
暗物质的第一个直接证据来自弗里茨·兹威基 (Fritz Zwicky)。
扩展的天体是星系团,它们被认为是束缚结构。
动力学质量是考虑星系团内每个星系计算出来的。
宇宙学 - 哈勃参数和密度参数
本章将讨论密度参数和哈勃参数。
哈勃参数
哈勃参数定义如下:
$$ H(t) \equiv \frac{da/dt}{a} $$
它衡量比例因子变化的速度。更一般地说,比例因子的演化由弗里德曼方程决定。
$$ H^2(t) \equiv \left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{kc^2}{a^2} + \frac{\wedge}{3} $$
其中,∧是宇宙常数。
对于平坦宇宙,k = 0,因此弗里德曼方程变为:
$$ \left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho + \frac{\wedge}{3} $$
对于物质主导的宇宙,密度变化如下:
$$ \frac{\rho_m}{\rho_{m,0}} = \left ( \frac{a_0}{a} \right )^3 \Rightarrow \rho_m = \rho_{m,0}a^{-3} $$
而对于辐射主导的宇宙,密度变化如下:
$$ \frac{\rho_{rad}}{\rho_{rad,0}} = \left ( \frac{a_0}{a} \right )^4 \Rightarrow \rho_{rad} = \rho_{rad,0}a^{-4} $$
目前,我们生活在一个物质主导的宇宙中。因此,考虑$\rho \equiv \rho_m$,我们得到:
$$ \left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho_{m,0}a^{-3} + \frac{\wedge}{3} $$
宇宙常数和暗能量密度关系如下:
$$ \rho_\wedge = \frac{\wedge}{8 \pi G} \Rightarrow \wedge = 8\pi G\rho_\wedge $$
由此,我们得到:
$$ \left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho_{m,0}a^{-3} + \frac{8 \pi G}{3} \rho_\wedge $$
此外,临界密度和哈勃常数关系如下:
$$ \rho_{c,0} = \frac{3H_0^2}{8 \pi G} \Rightarrow \frac{8\pi G}{3} = \frac{H_0^2}{\rho_{c,0}} $$
由此,我们得到:
$$ \left ( \frac{\dot{a}}{a} \right )^2 = \frac{H_0^2}{\rho_{c,0}}\rho_{m,0}a^{-3} + \frac{H_0^2}{\rho_{c,0}}\rho_\wedge $$
$$ \left ( \frac{\dot{a}}{a} \right )^2 = H_0^2\Omega_{m,0}a^{-3} + H_0^2\Omega_{\wedge,0} $$
$$ (\dot{a})^2 = H_0^2\Omega_{m,0}a^{-1} + H_0^2\Omega_{\wedge,0}a^2 $$
$$ \left ( \frac{\dot{a}}{H_0} \right )^2 = \Omega_{m,0}\frac{1}{a} + \Omega_{\wedge,0}a^2 $$
$$ \left ( \frac{\dot{a}}{H_0} \right )^2 = \Omega_{m,0}(1+z) + \Omega_{\wedge,0}\frac{1}{(1+z)^2} $$
$$ \left ( \frac{\dot{a}}{H_0} \right)^2 (1+z)^2 = \Omega_{m,0}(1+z)^3 + \Omega_{\wedge,0} $$
$$ \left ( \frac{\dot{a}}{H_0} \right)^2 \frac{1}{a^2} = \Omega_{m,0}(1 + z)^3 + \Omega_{\wedge,0} $$
$$ \left ( \frac{H(z)}{H_0} \right )^2 = \Omega_{m,0}(1+z)^3 + \Omega_{\wedge,0} $$
这里,$H(z)$是红移相关的哈勃参数。这可以修改为包含辐射密度参数$\Omega_{rad}$和曲率密度参数$\Omega_k$。修改后的方程为:
$$ \left ( \frac{H(z)}{H_0} \right )^2 = \Omega_{m,0}(1+z)^3 + \Omega_{rad,0}(1+z)^4+\Omega_{k,0}(1+z)^2+\Omega_{\wedge,0} $$
$$ 或,\left ( \frac{H(z)}{H_0} \right)^2 = E(z) $$
$$ 或,H(z) = H_0E(z)^{\frac{1}{2}} $$
其中,
$$ E(z) \equiv \Omega_{m,0}(1 + z)^3 + \Omega_{rad,0}(1+z)^4 + \Omega_{k,0}(1+z)^2+\Omega_{\wedge,0} $$
这表明哈勃参数随时间变化。
对于爱因斯坦-德西特宇宙,$\Omega_m = 1, \Omega_\wedge = 0, k = 0$。
将这些值代入,我们得到:
$$ H(z) = H_0(1+z)^{\frac{3}{2}} $$
这显示了爱因斯坦-德西特宇宙中哈勃参数的时间演化。
密度参数
密度参数$\Omega$定义为实际(或观测到的)密度ρ与临界密度$\rho_c$的比率。对于任何量$x$,相应的密度参数$\Omega_x$可以用数学方式表示为:
$$ \Omega_x = \frac{\rho_x}{\rho_c} $$
对于正在考虑的不同量,我们可以定义以下密度参数。
| 序号 | 数量 | 密度参数 |
|---|---|---|
| 1 | 重子 | $\Omega_b = \frac{\rho_b}{\rho_c}$ |
| 2 | 物质(重子+暗物质) | $\Omega_m = \frac{\rho_m}{\rho_c}$ |
| 3 | 暗能量 | $\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$ |
| 4 | 辐射 | $\Omega_{rad} = \frac{\rho_{rad}}{\rho_c}$ |
其中符号具有其通常的含义。
要点
比例因子的演化由弗里德曼方程决定。
H(z)是红移相关的哈勃参数。
哈勃参数随时间变化。
密度参数定义为实际(或观测到的)密度与临界密度的比率。
宇宙学 - 宇宙年龄
如前几章所述,哈勃参数的时间演化由下式给出:
$$ H(z) = H_0E(z)^{\frac{1}{2}} $$
其中z是红移,E(Z)为:
$$ E(z) \equiv \Omega_{m,0}(1+z)^3 + \Omega(1+z)^4 +\Omega_{k,0}(1+z)^2 + \Omega^{\wedge,0} $$
如果宇宙的膨胀是恒定的,那么宇宙的真实年龄如下:
$$ t_H = \frac{1}{H_0} $$
如果是物质主导的宇宙,即爱因斯坦-德西特宇宙,那么宇宙的真实年龄由下式给出:
$$ t_H = \frac{2}{3H_0} $$
比例因子和红移由下式定义:
$$ a=\frac{a_0}{1+z} $$
宇宙年龄根据宇宙学参数的推导如下。
哈勃参数由下式给出:
$$ H = \frac{\frac{da}{dt}}{a} $$
求导,我们得到:
$$ da = \frac{-dz}{(1+z)^2} $$
其中a0 = 1(比例因子的当前值)
$$ \frac{\mathrm{d} a}{\mathrm{d} t} = \frac{-1}{(1+z)^2} $$
$$ \frac{\mathrm{d} a}{\mathrm{d} t} = \frac{\mathrm{d} a}{\mathrm{d} t}\frac{\mathrm{d} z}{\mathrm{d} t} $$
$$ H = \frac{\dot{a}}{a} = \frac{\mathrm{d} a}{\mathrm{d} t}\frac{\mathrm{d} z}{\mathrm{d} t} \frac{1+z}{1} $$
$$ \frac{\dot{a}}{a} = \frac{-1}{1+z}\frac{\mathrm{d} z}{\mathrm{d} t}\frac{1}{1} $$
$$ H(z) = H_0E(z)^{\frac{1}{2}} $$
$$ dt = \frac{-dz}{H_0E(z)^{\frac{1}{2}}(1+z)} $$
如果我们想找到宇宙在任何给定红移'z'时的年龄,那么:
$$ t(z) = \frac{1}{H_0}\int_{\infty}^{z_1} \frac{-1}{E(z)^{\frac{1}{2}}(1+z)}dz $$
其中k是曲率密度参数,并且:
$$ E(z) \equiv \Omega_{m,0}(1+z)^3 + \Omega_{rad,0}(1+z)^4 + \Omega_{k,0}(1+z)^2 + \Omega_{\wedge,0} $$
要计算宇宙当前的年龄,取z1 = 0。
$$ t(z=0) = t_{age} = t_0 = \frac{1}{H_0}\int_{\infty}^{z_1} \frac{-1}{E(z)^{\frac{1}{2}}(1+z)}dz $$
对于爱因斯坦-德西特模型,即$\Omega_m = 1$,$\Omega_{rad} = 0$,$\Omega_k = 0$,$\Omega_\wedge = 0$,宇宙年龄的方程变为:
$$ t_{age} = \frac{1}{H_0}\int_{0}^{\infty} \frac{1}{(1+z)^{\frac{5}{2}}}dz $$
求解积分后,我们得到:
$$ t_H = \frac{2}{3H_0} $$
夜空就像一台宇宙时间机器。每当我们观测遥远的行星、恒星或星系时,我们看到的都是它在数小时、数百年甚至数千年前的样子。这是因为光以有限的速度(光速)传播,并且考虑到宇宙中的巨大距离,我们看到的不是物体现在的样子,而是光发射时它们的样子。在我们在地球上探测到光线和它最初由光源发射之间经过的时间被称为回溯时间 (tL(z1))。
因此,回溯时间由下式给出:
$$ t_1(z_1) = t_0-t(z_1) $$
爱因斯坦-德西特宇宙的回溯时间为:
$$ t_L(z) = \frac{2}{3H_0}\left [ 1- \frac{1}{(1+z)^{\frac{3}{2}}} \right ] $$
要点
每当我们观测遥远的行星、恒星或星系时,我们看到的都是它在数小时、数百年甚至数千年前的样子。
在我们在地球上探测到光线和它最初由光源发射之间经过的时间被称为回溯时间。
宇宙学 - 角直径距离
本章将了解角直径距离是什么以及它如何帮助宇宙学。
对于当前宇宙 −
$\Omega_{m,0} \: = \: 0.3$
$\Omega_{\wedge,0} \: = \: 0.69$
$\Omega_{rad,0} \: = \: 0.01$
$\Omega_{k,0} \: = \: 0$
到目前为止,我们已经学习了两种类型的距离:
自行距离 (lp)——光子从光源传播到我们的距离,即瞬时距离。
共动距离 (lc)——在不膨胀的空间中物体之间的距离,即在共动参考系中的距离。
距离作为红移的函数
考虑一个星系,它在时间t1辐射光子,该光子在t0被观察者探测到。我们可以将星系的自行距离写为:
$$ l_p = \int_{t_1}^{t_0} cdt $$
设星系的红移为z,
$$\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{1}{a^2}\frac{\mathrm{d} a}{\mathrm{d} t}$$
$$\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{\frac{\mathrm{d} a}{\mathrm{d} t}}{a}\frac{1}{a}$$
$$\therefore \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{H(z)}{a}$$
现在,星系在任意时刻t的共动距离为:
$$l_c = \frac{l_p}{a(t)}$$
$$l_c = \int_{t_1}^{t_0} \frac{cdt}{a(t)}$$
用z表示为:
$$l_c = \int_{t_0}^{t_1} \frac{cdz}{H(z)}$$
有两种方法可以求距离,如下:
通量-光度关系
$$F = \frac{L}{4\pi d^2}$$
其中d是光源的距离。
光源的角直径距离
如果我们知道光源的大小,它的角宽度就可以告诉我们它与观测者的距离。
$$\theta = \frac{D}{l}$$
其中l是光源的角直径距离。
θ是光源的角大小。
D是光源的大小。
考虑一个大小为D,角大小为dθ的星系。
我们知道:
$$d\theta = \frac{D}{d_A}$$
$$\therefore D^2 = a(t)^2(r^2 d\theta^2) \quad \because dr^2 = 0; \: d\phi ^2 \approx 0$$
$$\Rightarrow D = a(t)rd\theta$$
将r改为rc,即星系的共动距离,我们有:
$$d\theta = \frac{D}{r_ca(t)}$$
这里,如果我们选择t = t0,我们将最终测量到星系的当前距离。但是D是在光子发射时测量的。因此,使用t = t0会得到星系距离更大的值,从而低估了它的尺寸。因此,我们应该使用时间t1。
$$\therefore d\theta = \frac{D}{r_ca(t_1)}$$
将此与之前的结果进行比较,我们得到:
$$d_\wedge = a(t_1)r_c$$
$$r_c = l_c = \frac{d_\wedge}{a(t_1)} = d_\wedge(1+z_1) \quad \because 1+z_1 = \frac{1}{a(t_1)}$$
因此,
$$d_\wedge = \frac{c}{1+z_1} \int_{0}^{z_1} \frac{dz}{H(z)}$$
dA是物体的角直径距离。
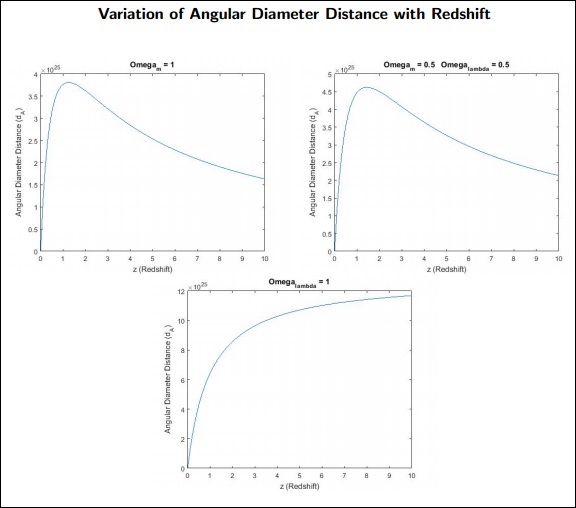
要点
如果我们知道光源的大小,它的角宽度就可以告诉我们它与观测者的距离。
固有距离是光子从光源传播到我们的距离。
共动距离是在不膨胀的空间中物体之间的距离。
宇宙学 - 光度距离
如前章所述,红移为z的光源的角直径距离由下式给出:
$$d_\wedge (z_{gal}) = \frac{c}{1+z_{gal}}\int_{0}^{z_{gal}} \frac{1}{H(z)}dz$$
$$d_\wedge(z_{gal}) = \frac{r_c}{1+z_{gal}}$$
其中$r_c$是共动距离。
光度距离取决于宇宙学,它被定义为观测到的通量f来自一个物体的距离。
如果已知远处物体的固有光度$d_L$,我们可以通过测量通量$f$来计算其光度,该通量由下式确定:
$$d_L(z) = \sqrt{\frac{L}{4\pi f}}$$
光子能量发生红移。
$$\frac{\lambda_{obs}}{\lambda_{emi}} = \frac{a_0}{a_e}$$
其中$\lambda_{obs}, \lambda_{emi}$分别是观测波长和发射波长,$a_0, a_e$分别是相应的比例因子。
$$\frac{\Delta t_{obs}}{\Delta t_{emi}} = \frac{a_0}{a_e}$$
其中$\Delta_t{obs}$是观测到的光子时间间隔,而$\Delta_t{emi}$是发射光子的时间间隔。
$$L_{emi} = \frac{nhv_{emi}}{\Delta t_{emi}}$$
$$L_{obs} = \frac{nhv_{obs}}{\Delta t_{obs}}$$
$\Delta t_{obs}$将比$\Delta t_{emi}$花费更多时间,因为探测器应该接收所有光子。
$$L_{obs} = L_{emi}\left ( \frac{a_0}{a_e} \right )^2$$
$$L_{obs} < L_{emi}$$
$$f_{obs} = \frac{L_{obs}}{4\pi d_L^2}$$
对于非膨胀宇宙,光度距离与共动距离相同。
$$d_L = r_c$$
$$\Rightarrow f_{obs} = \frac{L_{obs}}{4\pi r_c^2}$$
$$f_{obs} = \frac{L_{emi}}{4 \pi r_c^2}\left ( \frac{a_e}{a_0} \right )^2$$
$$\Rightarrow d_L = r_c\left ( \frac{a_0}{a_e} \right )$$
我们正在寻找光度距离$d_L$来计算发射物体$L_{emi}$的光度:
解释:如果我们知道任何星系的红移z,我们可以求出$d_A$,并由此计算出$r_c$。这用于求出$d_L$。
如果$d_L ! = r_c(a_0/a_e)$,那么我们无法从$f_{obs}$中找到$L_{emi}$。
光度距离$d_L$和角直径距离$d_A$之间的关系。
我们知道:
$$d_A(z_{gal}) = \frac{d_L}{1+z_{gal}}\left ( \frac{a_0}{a_e} \right )$$
$$d_L = (1 + z_{gal})d_A(z_{gal})\left ( \frac{a_0}{a_e} \right )$$
光子发射时的比例因子由下式给出:
$$a_e = \frac{1}{(1+z_{gal})}$$
当前宇宙的比例因子为:
$$a_0 = 1$$
$$d_L = (1 + z_{gal})^2d_\wedge(z_{gal})$$
选择$d_L$还是$d_A$?
对于已知大小和红移的星系,为了计算它有多大,使用$d_A$。
如果有一个给定视星等的星系,那么要找出它有多大,就使用$d_L$。
示例:如果给定两个红移相等(z = 1)的星系,并且在天空平面中它们相隔2.3角秒,那么这两个星系之间的最大物理距离是多少?
为此,使用$d_A$如下:
$$d_A(z_{gal}) = \frac{c}{1+z_{gal}}\int_{0}^{z_{gal}} \frac{1}{H(z)}dz$$
其中z = 1,根据星系的宇宙学参数替换H(z)。
要点
光度距离取决于宇宙学。
如果已知远处物体的固有光度$d_L$,我们可以通过测量通量f来计算其光度。
对于非膨胀宇宙,光度距离与共动距离相同。
光度距离总是大于角直径距离。
宇宙学 - Ia型超新星
对于任何给定的红移 (z),我们有两个距离值:
- 角直径距离 (dA)
- 光度距离 (dL)
宇宙中没有“宇宙学”距离的唯一定义。距离的选择取决于应用的目的和方便性。
为了检验物体角大小随红移变化的预测趋势,需要在天空使用标准尺寸的标尺。这应该是一个物体,它:
非常明亮,因此可以在 z > 1 时被探测到。
非常大,因此我们可以分辨其角大小。
在宇宙学上重要的时期内(z ∼ 1对应于大约7 Gyr 的回溯时间)没有形态演化。
一些天体(如cD星系)满足前两个标准。但几乎所有天体都被发现会随着时间发生形态演化。一般来说,天体物理天体(延展光源)过去往往较小,因为它们仍在形成。
光度距离
光度距离取决于宇宙学。光度距离对宇宙学的依赖性使其成为宇宙学参数的有用度量。
如果我们能找到一个不会内在演化并且从局部宇宙到高红移宇宙都存在的标准烛光,那么就可以估计宇宙学参数。
标准烛光是指其光度在不同光源之间没有差异的光源。前提是标准烛光估计光度的任何差异都必须是由于宇宙学造成的。Ia型超新星就是这样的一个烛光。
Ia型超新星 (SNe)
这些是白矮星在从其伴星(红巨星或类似的主序星)吸积足够质量后爆炸的结果,在一个双星系统中。在红巨星比白矮星的洛希瓣距离更近之后,质量转移开始,最终白矮星爆炸产生巨大的能量,没有留下核心。这些被称为Ia型超新星。一个星系中Ia型超新星爆炸的典型速率是每世纪一次。
对Ia型超新星的搜寻一直在进行,不同的团队参与其中:
- 高红移超新星搜寻团队(布莱恩·施密特、亚当·里斯等人)
- 超新星宇宙学项目(索尔·珀尔马特等人)
还有一个名为卡内基超新星项目的研究团队,他们给出了类似的结果。
不同团队结果的相似性表明了Ia型超新星的宇宙学性质。因此,它们是有效的标准烛光。
要点
宇宙中没有“宇宙学”距离的唯一定义。
角直径距离和光度距离是最常用的。
标准烛光是指其光度在不同光源之间没有差异的光源。
Ia型超新星满足作为标准烛光的标准。
宇宙学 - 宇宙微波背景
CMB(宇宙微波背景)基本上是由物质和辐射处于平衡状态时的光子构成的。到20世纪20年代,膨胀宇宙的思想已被接受,并可以回答一些问题。但关于较重元素的丰度和丰度的疑问仍未得到解答。此外,膨胀宇宙意味着物质的密度应该下降到0。
1948年,乔治·伽莫夫和拉尔夫·阿尔珀利用“大爆炸”解释了较重元素的起源和丰度。他们与罗伯特·赫尔曼一起预测了“遗迹辐射”的存在,即“大爆炸”后剩余的辐射。这种残余辐射的预测温度在50-6 K之间。1965年,罗伯特·迪克、吉姆·皮布尔斯和戴维·威尔金森以及阿莫·佩里齐亚斯研究小组通过实验探测到了CMB。
早期的宇宙非常热,能量太高,物质无法保持中性。因此,物质处于电离状态——等离子体。辐射(光子)和物质(等离子体)主要通过以下三个过程相互作用。
康普顿散射——(主要相互作用过程)高能光子和低能带电粒子之间的非弹性散射。
汤姆逊散射——光子被自由带电粒子弹性散射。
逆康普顿散射——高能带电粒子与低能光子。这些相互作用最终导致物质和辐射达到热平衡。
热平衡
在热平衡中,辐射服从普朗克能量分布,
$$B_v(T) = \frac{2hv^3}{c(e^{hv/k_BT}-1)}$$
在此期间,由于相互作用非常频繁,光子的平均自由程非常小。宇宙对辐射是不透明的。早期宇宙是辐射主导的。宇宙以物质和辐射达到热平衡并且它们的能量密度变得相等的方式演化。这可以从显示密度随比例因子变化的图表中看出。让我们找出物质和辐射达到平衡时的比例因子(时间)(a(t))。
$$\rho_m \propto \frac{1}{a^3}, \: \rho_r \propto \frac{1}{a^4}$$
$$\frac{\rho_{m,t}}{\rho_{r,t}} = \frac{\Omega_{m,t}}{\Omega_{r,t}} = \frac{\Omega_{m,0}}{\Omega_{r,0}}a(t)$$
在平衡时,
$$\frac{\rho_{m,t}}{\rho_{r,t}} = \frac{\Omega_{m,t}}{\Omega_{r,t}} = 1$$
$$\Rightarrow \frac{\Omega_{m,0}}{\Omega_{r,0}}a(t) = 1 \: \Rightarrow a(t) = 2.96 \times 10^{-4}$$
使用$\Omega_{m,0} = 0.27$和$\Omega_{r,0} = 8 \times 10^{−5}$。对应于该比例因子的红移由下式给出:
$$z = 1/a(t)-1 \approx 3375$$
由于宇宙膨胀,辐射能密度下降,从而宇宙开始冷却。随着光子能量的降低,中性原子开始形成。因此,在大约红移1300左右,中性氢开始形成。这个时期的温度接近3000K。
物质与辐射之间的相互作用变得非常不频繁,因此宇宙开始变得对辐射透明。这段时期被称为“最后散射面”,因为光子的平均自由程变得非常大,导致此后几乎没有发生散射。它也被称为“宇宙光球”。
要点
CMB由物质和辐射处于平衡状态时期的光子构成。
早期宇宙非常热,能量太高,物质无法保持中性,因此它以电离物质——等离子体的形式存在。
康普顿散射、汤姆逊散射、逆康普顿散射是当时的三种物质-辐射相互作用过程。
宇宙演化使得物质和辐射达到热平衡。
解耦时的CMB温度
我们首先应该了解什么特征决定了解耦。我们知道能量高得多,以至于物质只以电离粒子的形式存在。因此,在解耦和复合时期,能量必须下降才能允许氢的电离。可以进行近似计算来估计解耦时的温度。
计算过程如下:
首先,只考虑基态氢的电离。
$$hv \approx k_BT$$
$$\therefore T \approx \frac{hv}{k_B}$$
对于基态氢的电离,hν为13.6 eV,kB为玻尔兹曼常数8.61 × 10−5 eV/K,这表明温度为1.5 × 105 开尔文。
这实质上告诉我们,如果温度低于1.5 × 105 K,中性原子就可以开始形成。
我们知道光子与重子的比率约为5 × 1010。因此,即使在光子数量减少的图表尾部,仍然会有足够的光子来电离氢原子。此外,电子和质子的复合并不能保证基态氢原子。激发态需要较低的能量来电离。因此,应该针对具体情况进行严格的统计分析才能获得准确的值。计算结果将温度设定为约3000K。
为了解释起见,我们考虑将氢激发到第一激发态的情况。能量大于ΔE的光子数Nγ (> ΔE)与光子总数Nγ的比率的一般表达式为:
$$\frac{N_\gamma(> \Delta E)}{N_\gamma} \propto e^{\frac{-\Delta E}{kT}}$$
对于将氢激发到第一激发态的情况,ΔE为10.2 eV。现在,如果我们考虑一个非常保守的数字,即每个重子至少有一个能量大于10.2 eV的光子(记住比率为5 × 1010),我们从公式3中得到温度为4800 K(代入Nγ(> ΔE) = Np)。
这是产生第一激发态中性氢原子群的温度。电离该态所需的温度明显较低。因此,我们得到了比1.5 × 105 K更好的估计值,更接近于公认值3000 K。
红移-温度关系
为了理解红移和温度之间的关系,我们采用以下两种方法,如下所述。
方法1
从维恩位移定律,我们知道
$$\lambda_mT = 常数$$
为了将其与红移联系起来,我们使用:
$$1+z = \frac{\lambda_0}{\lambda_e}$$
由于$λ_oT_o = λ_eT(z)$,我们得到:
$$T(z) = T_0\frac{\lambda_0}{\lambda_e} = T_0(1+z)$$
将To设置为当前值3K,我们可以获得给定红移下的温度值。
方法2
就频率而言,我们知道:
$$v_0 = \frac{v_e}{1+z}$$
$$B_vdv = \frac{2hv^3}{c^2} \frac{dv}{e^{hv/kT}-1}$$
这告诉我们一定能量区间内光子的净能量,hν是单个光子的能量。因此,我们可以通过Bνdν/hν获得光子数。
如果$n_{νo}$代表现在,$n_{νe}$代表发射,我们得到:
$$\frac{n_{v_e}}{n_{v_0}} = (1+z)^3$$
简化后,我们得到:
$$n_{v_0} =\frac{2v_c^2}{c^2}\frac{dv_c}{e^{hv/kT}-1}\frac{1}{(1+z)^3}=\frac{2v_0^2}{c^2}\frac{dv_c}{e^{hv/kT}-1}$$
这再次给出维恩位移定律,因此可以得出结论:
$$T(z) = T_0\frac{\lambda_0}{\lambda_e} = T_0(1+z)$$
要点
- 早期宇宙非常热,约为3000K。
- 目前的测量结果表明宇宙的温度接近3K。
- 我们回溯的时间越远,温度就成比例地升高。
CMB辐射的各向异性与COBE卫星
本章将讨论CMB辐射的各向异性和COBE(宇宙背景探测器)。
CMB中的主要各向异性
为了理解来自太空的观测结果和宇宙微波背景辐射中的主要各向异性,让我们考虑以下方程,并按如下所示理解它。
CMB光子数密度 (nγ,0)
$$n_{\gamma,0} = \frac{总能量密度}{光子的特征能量}$$
$$n_{\gamma,0} = \frac{aT_0^4}{k_BT_0}$$
其中$k_B$是玻尔兹曼常数,$T_0$是宇宙目前的温度。
使用目前的温度$(T_0)$为2.7 K,我们得到当前的CMB光子数密度为400 cm−3。
在大的尺度上,宇宙恒星光子的数密度要小得多(≈10−3 cm−3)。
重子与光子的比率 (η)
如果来自星系的恒星贡献(与CMB混合)可以忽略不计,则重子与质子的比率为:
$$\eta = \frac{n_{b,0}}{n_{\gamma,0}}$$
目前的值约为5 × 10−10。由于光子数密度和重子数密度都与a−3成正比,因此η不会随时间变化。
能量密度
与数密度相反,目前物质能量密度比光子能量密度更占主导地位。
重子物质的能量密度 = $\rho_{b,0}c^2 = 0.04\rho_cc^2 = 2 × 10^{−9} ergcm^{−3}$。而辐射的能量密度 = $aT_0^4 = 4 \times 10^{−13}ergcm{−3}$。
CMB辐射的各向同性
彭齐亚斯和威尔逊发现,在观测限度内,CMB是各向同性的。限度是仪器的低角分辨率和灵敏度。他们在地球上进行观测,因此无法通过所有光谱进行观测,因为大气中的水蒸气吸收了从1mm到1m的许多波长。因此,CMB不能被认为是一个光谱。
CMB被认为是旋转不变的(各向同性的)。由于存在物质和辐射处于平衡状态的时期,因此宇宙中结构的形成是无法解释的。由于物质的分布不是各向同性的,而是像宇宙网一样聚集在一起,中间有巨大的空洞,因此CMB被认为具有河外起源。
但是,随着太空观测的开始,发现了CMB中的各向异性,这导致人们推断这些物质的各向异性导致了结构的形成。
从太空观测CMB辐射
发射用于观测CMB的主要卫星有:
宇宙微波背景探测器 (COBE, 1989)
威尔金森微波各向异性探测器 (WMAP, 2001) 和
普朗克 (2009).
COBE(宇宙背景探测器)
COBE主要有两个仪器。它们是远红外绝对光谱仪(FIRAS)和差分微波辐射计(DMR天线)。FIRAS测量CMB的强度作为沿任何特定方向的波长的函数。而DMR有3个天线来测量来自三个不同方向的CMB强度的差异。以下要点为我们提供了有关FIRAS和DMR的更多信息。
来自FIRAS的CMB观测表明,CMB辐射对应于T = 2.72528±0.00065 K的黑体光谱。
DMR测量天空所有方向的三个频率(31.5 GHz、53 GHz、90 GHz)。
DMR观测中的“红色蝙蝠侠符号”是来自前景发射(银河系弥漫同步辐射)的噪声。
观测中的强度变化对应于温度变化。热点和冷点的存在证明了CMB辐射是各向异性的。
这种各向异性一定存在于解耦时期,因为CMB没有畸变。因此,物质应该有一些密度高于其他物质的区域。
COBE结果
CMB光谱(强度作为能量的函数)几乎是完美的黑体,对应于T = 2.7 K。CMB辐射的比强度对于所有方向几乎相同。证实了宇宙在大尺度上是各向同性的(验证了我们对宇宙原理的假设)。
对数据的分析表明,在COBE(DMR)的分辨率下,CMB光谱中存在温度各向异性(“涨落”)。
COBE、WMAP、普朗克的分辨率
COBE上的DMR仪器的极限(最大)空间分辨率约为7度。
威尔金森微波各向异性探测器(WMAP)的平均分辨率约为0.7度。
普朗克卫星的角分辨率约为10角分。
要点
宇宙恒星光子的数密度远小于CMB光子的数密度。
我们生活在一个物质主导的宇宙中,因为物质能量密度高于光子能量密度。
COBE、WMAP、普朗克都是为了测量和量化CMB中的各向异性而做出的努力。
宇宙中结构的形成是CMB各向异性的结果。
宇宙学——模拟CMB各向异性
当我们观察精细校正的全天CMB图时,会发现大量的 foreground contamination(前景污染),这是一种地图中的**各向异性**。我们可以看到这些前景辐射来自银河系。CMB的强度沿银道面较高,并随着远离银道面而减弱。其中,我们可以观测到二次各向异性,即来自星系的同步辐射。这些辐射构成了前景污染。为了观察来自天空的CMB辐射,我们需要减去这些前景辐射。
下图显示了带有前景辐射的CMB。
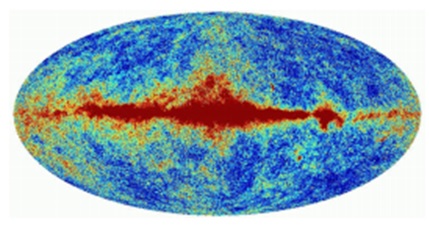
偶极各向异性
在CMB全天图中还发现了另一种各向异性,称为偶极各向异性。它与早期宇宙无关。这可以用球谐函数表示。如果球面上存在某种模式,并且我们想用数学函数对其进行映射,则可以使用三角函数。因此,当我们进行映射时,它可以是单极——各个方向都相同,或者偶极——旋转180度时属性发生反转。类似地,我们还有四极等等。对于复杂的模式,它可以表示为这些单极、偶极、四极等的总和。
CMB模型认为,全天图中各向异性的主要来源之一是这种偶极各向异性,但它并非CMB的原始模型。这可以在下面的图像中看到。
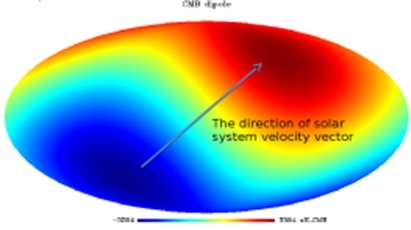
我们看到的偶极方向并非随机方向。偶极各向异性具有方向性。我们沿着特定方向观察CMB强度。这个方向是由太阳系速度矢量决定的。地球的速度可以用相对于太阳或银河系中心来表示。在地球运动的方向上,我们观察到蓝移和红移,偶极位于此方向。
上图具有典型的偶极外观,因为我们的星系正在特定方向上运动。结果是——天空的一侧看起来是红移的,而天空的另一侧看起来是蓝移的。在这种情况下,红移意味着光子的波长更长=更冷(所以与它们的名称相反,它们在上图中看起来是蓝色的)。
我们可以说,地球相对于太阳/银河系中心/天空中的CMB在给定时刻沿特定方向运动。然后,如果我们观察任何角度并测量CMB的温度,它都会有所不同。这是因为我们正在测量处于蓝移或红移状态的光子,并且取决于天空中光子的视线。
要点
CMB全天图中的前景污染被称为CMB的各向异性。
这些辐射来自我们自己的银河系。
两种各向异性是:偶极各向异性和角功率谱各向异性。
偶极各向异性在特定方向上,而角功率谱各向异性则遍布各地。
最后散射面上的视界长度
视界长度是光子从“大爆炸”到“复合时期”所传播的距离。角谱的第一个峰值位于θ = 1°(l = 180),这是一个非常特殊的长度尺度。
两点之间的固有距离由下式给出:
$$r_p = \int_{0}^{t}cdt$$
当我们取时间范围t = 0到t = trec时,则
$$r_H = \int_{0}^{t_{rec}}cdt$$
其中$r_H$是固有视界距离。
现在,我们知道:
$$\dot{a} = \frac{\mathrm{d} a}{\mathrm{d} t}$$
$$dt = \frac{da}{\dot{a}}$$
当t = 0时,a = 0。
则t = trec,a = a0 / (1 + zrec)。
因此,我们可以写成:
$$r_H(z_{rec})=\int_{0}^{a_{rec}} c\frac{da}{aH}$$
$$H(a_{rec}) = H(z_{rec}) = H_0\sqrt{\Omega_{m,0}}a^{-3/2}$$
在**复合时期**,宇宙是物质主导的。即,**Ωrad << Ωmatter**。因此,辐射项被忽略。
$$r_H(z_{rec}) = \frac{c}{H_0\sqrt{\Omega_{m,0}}}\int_{0}^{a_{rec}} \frac{da}{a^{-1/2}}$$
$$r_H(z_{rec}) = \frac{2c}{3H_0\sqrt{\Omega_{m,0}}}\frac{1}{(1+z_{rec})^{3/2}}$$
$$\theta_H(rec) = \frac{r_H(z_{rec})}{d_A(z_{rec})}$$
如果我们将所有已知值代入方程,则等于0.5度。
从最后散射面来看,**电磁辐射**是不透明的。任何两点如果不位于彼此的视界内,则不必具有相同的属性。因此,它会给出不同的温度值。
我们可以在此表面上找到两点,它们彼此不相交,这意味着在某一点上宇宙膨胀速度超过光速,这就是膨胀的暴胀模型。
要点
视界长度是光子从“大爆炸”到“复合时期”所传播的距离。
在复合时期,宇宙是物质主导的。
从最后散射面来看,电磁辐射是不透明的。
宇宙学 - 太阳系外行星探测
**天体生物学**是研究宇宙中生命起源、进化、分布和未来的学科。它关注于发现和探测**太阳系外行星**。
**天体生物学**探讨以下几点:
生命如何开始和进化?(生物学 + 地质学 + 化学 + 大气科学)
地球以外是否存在有利于生命存在的星球?(天文学)
地球生命的未来将会怎样?
**天文学**探讨以下几点:
如何探测其他恒星周围的行星系统?
其中一种方法是直接成像,但这项任务非常困难,因为与恒星相比,行星是极其微弱的光源,而且它们发出的微弱光线往往会淹没在母恒星的光辉中。
当行星更靠近其母恒星且温度较高时,对比度更好,因此它会发出强烈的红外辐射。我们可以在红外区域拍摄图像。
太阳系外行星探测技术
探测太阳系外行星最有效的方法如下。这些方法在后续章节中也将详细解释。
径向速度法
它也称为多普勒方法。在这个方法中:
恒星-行星系统绕它们的质心旋转,恒星会摆动。
摆动可以通过以下方式检测:
周期性的红/蓝移。天体测量——非常精确地测量天体的位置。
凌日法
凌星法(开普勒太空望远镜)用于确定大小。与双星系统不同,行星导致恒星亮度下降通常非常小。
直接成像
使用望远镜对行星成像。
让我们来看一个关于径向速度法的案例研究。
案例研究
本案例研究的对象是圆形轨道,并且轨道的平面垂直于天空平面。两者围绕质心旋转所需的时间相同。它等于两次红移或蓝移之间的时间差。
请考虑下图。
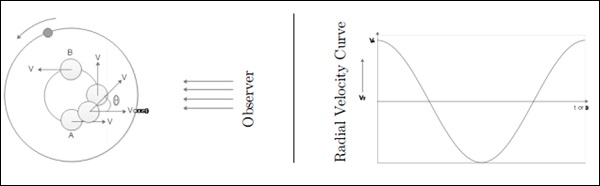
在A和C点——测量到全速度。在C点,速度为零。
Vrmax = V*是恒星的真实速度。
P是恒星和行星的周期。
θ是轨道的相位。
恒星质量 - M*,轨道半径a*,行星质量**mp**。
根据质心方程:
$$m_p a_p = M_\ast a_\ast$$
根据速度方程:
$$V_\ast = \frac{2\pi a_\ast}{P}$$
$$\Rightarrow a_\ast = \frac{PV_\ast}{2\pi}$$
根据**开普勒定律**:
$$P^2 = \frac{4\pi^2a_p^3}{GM_\ast}$$
$$\Rightarrow a_p = \left ( \frac{P^2GM_\ast}{4\pi^2} \right)^{1/3}$$
根据上述方程,我们得到:
$$\Rightarrow m_p = \left( \frac{P}{2\pi G} \right)^{1/3}M_\ast^{2/3}V_\ast$$
我们得到:mp、ap和a*。
上述方程偏向于靠近恒星的大质量行星。
要点
天体生物学是研究宇宙中生命起源、进化、分布和未来的学科。
探测太阳系外行星的技术包括:径向速度法、凌星法、直接成像法等。
摆动可以通过周期性的红/蓝移和天体测量来检测。
径向速度法偏向于探测靠近恒星的大质量行星。
宇宙学 - 径向速度法
在上一章中,讨论了对于轨道平面和天空平面垂直的情况下的径向速度法(针对圆形轨道)。在这里,我们处理另一种情况,即轨道平面和天空平面不垂直的情况(针对圆形轨道)。
当轨道平面与天空平面成一定角度(不垂直)时,我们有以下情况:
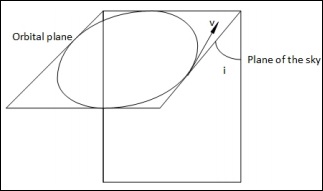
在这种情况下,当它们垂直时,我们有两个点可以测量真实速度。但在这里,这是不可能的。在所有点上,我们只能测量真实速度**v**的一个分量。
$$v_r = v \:sin(i)cos(\theta)$$
其中**θ**是轨道的相位,它是一个时间相关的量。另一方面,倾角**i**与时间无关。因此:
$$(v_r)_{max} = v\: sin(i)$$
观测到的径向速度曲线将具有以下形式:
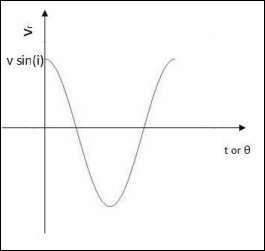
当轨道平面垂直于天空时:
$$m_p = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}}(M_\ast)^{\frac{2}{3}}v$$
其中**mp、P、G、M∗**分别代表行星质量、轨道周期、万有引力常数和恒星质量。但在这种情况下,我们应该将其修改如下:
$$m_psin(i) = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}} (M_\ast)^{\frac{2}{3}}(v_r)_{max}$$
但是,找到i的值是一项困难的任务。我们可以使用凌星法对i的值施加某些约束。行星在恒星和地球之间经过称为凌星。我们可以通过观察凌星和光变曲线中观测通量的显著下降来获得光变曲线,这意味着i接近90度。如果不满足这些条件,我们就无法对i的值有任何了解。那么我们找到的mp值可以作为行星质量的下限,因为它实际上是mp sin(i),而sin(i) ≤ 1。
总之,径向速度法比凌星法更方便,因为径向速度可以随时测量,而凌星测量只能在凌星期间进行,而凌星持续时间可能不长。
要点
径向速度法无法确定行星轨道的倾角。
径向速度法优于凌星法,因为径向速度可以始终测量,而凌星则不然。
凌星是短暂的,很容易错过。
宇宙学 - 凌星法
凌星法**(开普勒太空望远镜)**用于确定大小。与双星系统不同,行星导致恒星亮度下降通常非常小。
**F0**是行星掩食恒星之前恒星的通量。
**F1**是整个行星都在恒星前面后的通量。
下图将用于所有计算。
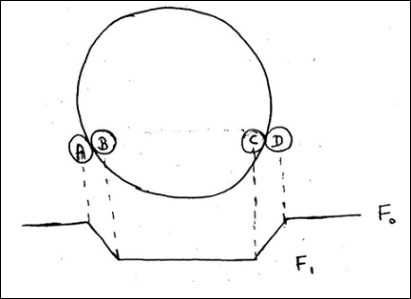
$$\frac{F_0 - F_1}{F_0} = \frac{\pi r_p^{2}}{\pi R^2_\ast}$$
$$\frac{\Delta F}{F} \cong \frac{r^2_p}{R^2_\ast}$$
$$\left ( \frac{\Delta F}{F} \right )_{earth} \cong 0.001\%$$
$$\left ( \frac{\Delta F}{F} \right )_{jupiter} \cong 1\%$$
地面望远镜难以做到这一点。这是通过哈勃望远镜实现的。
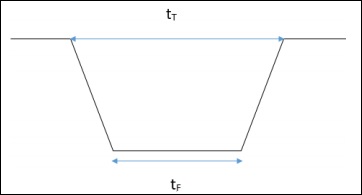
这里,tT是A点和D点之间的时间,tF是B点和C点之间的时间。
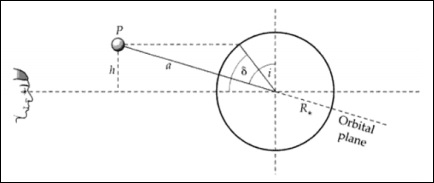
凌星的几何形状与系统的倾角**i**有关。凌星纬度和倾角可以互换。
根据上图,我们可以写成:
$$\frac{h}{a} = cos(i)$$
$$\frac{h}{R_\ast} = sin(\delta)$$
$$cos(i) = \frac{R_\ast sin(\delta)}{a}$$
$$y^2 = (R_\ast + R_p)^2 - h^2$$
$$y = [(R_\ast + R_p)^2 - h^2]^{\frac{1}{2}}$$
$$sin(\theta) = \frac{y}{a}$$
$$θ = arcsin\left [ \frac{(R_\ast + R_p)^2 - a^2cos^2(i)}{a^2} \right ]^{\frac{1}{2}}$$
$$t_T = \frac{P}{2\pi} \times 2θ$$
这里,$t_T$ 是凌星发生所占时间的比例,$(2θ/2π)$ 是凌星发生所占角度的比例。
$$sin(\frac{t_Tπ}{P}) = \frac{R_\ast}{a}\left [ \left ( 1+ \frac{R_p}{R_\ast}\right )^2 - \left ( \frac{a}{R_\ast}cos(i)\right )^2 \right ]^{\frac{1}{2}}$$
通常情况下,a >> R∗ >> Rp。因此,我们可以写成:
$$sin(\frac{t_Tπ}{P}) = \frac{R_\ast}{a}\left [ 1- \left ( \frac{a}{R_\ast}cos(i) \right )^2\right ]^{\frac{1}{2}}$$
这里,P 是两次连续凌星之间的时间间隔。凌星时间与轨道周期相比非常短。因此,
$$t_T = \frac{P}{π}\left [ \left ( \frac{R_\ast}{a}\right )^2 - cos^2(i)\right ]^{\frac{1}{2}}$$
这里,tT, P, R∗ 是可观测量,a 和 i 需要求解。
现在,
$$sin(\frac{t_Fπ}{P}) = \frac{R_\ast}{a}\left [\left (1 - \frac{R_p}{R_\ast} \right )^2 - \left ( \frac{a}{R_\ast}cos\:i \right )^2\right ]^{\frac{1}{2}}$$
其中,$y^2 = (R_\ast − R_p)^2 − h^2$。
设,
$$\frac{ΔF}{F} = D = \left ( \frac{R_p}{R_\ast} \right )^2$$
现在,我们可以表示为:
$$\frac{a}{R_\ast} = \frac{2P}{π} D^{\frac{1}{4}}(t^2_T - t^2_F)^{-\frac{1}{2}}$$
对于主序星,
$$R_\ast ∝ M^\alpha_\ast$$
$$\frac{R_\ast}{R_0} ∝ \left ( \frac{M_\ast}{M_0}\right )^\alpha$$
这给出R∗ 的值。
因此,我们也得到了 ‘a’ 的值。
所以,我们得到了 ‘Rp’,‘a’ 和 ‘i’。
对于所有这些,
$$h ≤ R_\ast + R_p$$
$$a\: cos\: i ≤ R_\ast + R_p$$
即使对于 i ≈ 89 度,凌星持续时间也非常短。行星必须非常靠近才能获得足够的凌星时间。这给 ‘i’ 提供了严格的约束。一旦我们得到 ‘i’,我们就可以从视向速度测量中推导出 ‘mp’。
这种通过凌星法进行的探测被称为偶然探测,即观测到凌星的概率。凌星概率(观测概率)的计算如下所示。
凌星概率与两种极端凌星构型所描绘出的立体角有关,即:
$$行星立体角 = 2π \left ( \frac{2R_\ast}{a} \right )$$
以及在半长轴 a 处的总立体角,或:
$$球体立体角 = 4π$$
概率是这两个面积的比率:
$$= \frac{有利方向所覆盖的天区面积}{所有可能的轨道方向所覆盖的天区面积}$$
$$= \frac{4π a_pR_\ast}{4π a^2_p} = \frac{R_\ast}{a_p} \quad \frac{空心圆柱体面积}{球体面积}$$
此概率与观测者无关。
要点
- 凌星法(开普勒太空望远镜)用于确定大小。
- 凌星法探测是偶然探测。
- 行星必须非常靠近才能获得足够的凌星时间。
- 凌星概率与行星的立体角有关。
- 此概率与观测者的参考系无关。
宇宙学 - 系外行星性质
2004年,首张系外行星的直接图像拍摄的是一颗质量为3-10 M木星的行星,它围绕着一颗质量为25 M木星的褐矮星 (2M1207) 运行。视向速度法、凌星法、引力微透镜法、成像法、天体测量法等技术已被用于探测系外行星。探测数量每年都在增加。
大约到2010年之前,视向速度法被广泛使用,但现在大多数探测都是通过凌星法完成的。2014年探测数量激增,那是开普勒太空望远镜 (KST) 开始提供结果的时候。
质量-周期分布表明,视向速度法更容易偏向于探测具有更大周期的巨型行星,而使用凌星法,只能探测到周期较短的行星,如下面的图像所示(资料来源:NASA 系外行星档案)。
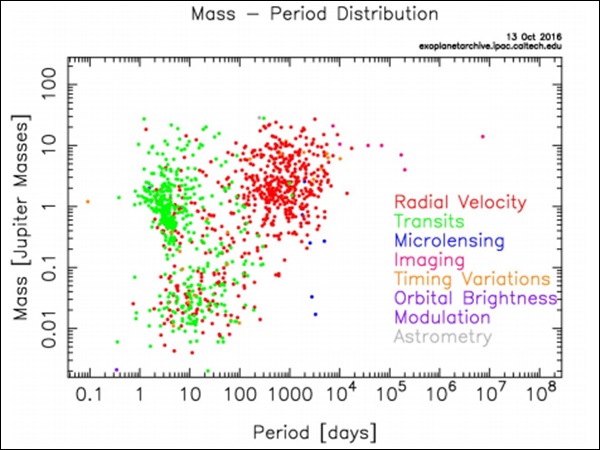
自从KST出现以来,较小质量行星的探测数量大幅增加。从下图可以看出这一点。KST探测到的行星分为两类:被称为“热木星”的热巨行星和被称为“热超级地球”(因为它们的质量大于地球)的较小质量行星。
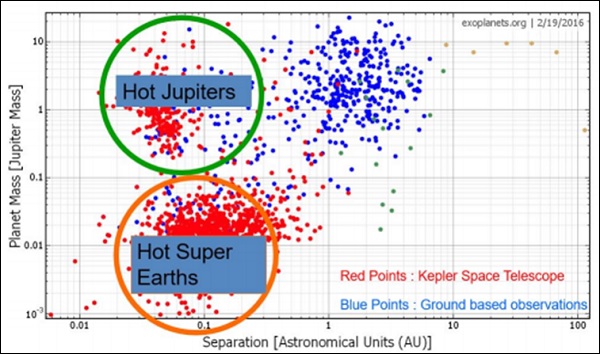
当我们绘制探测到的系外行星数量与它们到我们的距离的关系图时,我们发现大多数这些行星都在2kpc以内,这远在我们银河系内。也许宇宙中行星并不罕见,因为我们的探测仅限于宇宙非常小的一部分中某种类型的行星。
行星是由星周盘或原行星盘形成的。如果行星是在恒星形成过程中产生的副产品,那么宇宙中行星的数量可能超过宇宙中恒星的数量!!
宜居带
宜居带可以定义为恒星周围水可以以液态形式存在的一个区域。考虑一颗距离恒星 $a_p$ 的行星,如下图所示。计算行星温度的一种简单方法如下所示。
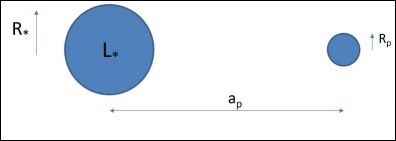
$$\left ( \frac{L_\ast}{4π a^2_p} \right )π R^2_p(1 - A) = 4π R^2_p σ T^4_p$$
以及
$$\frac{L_\ast}{4π R^2_\ast} = σ T^4_\ast$$
$$\therefore T_p = (1 - A)T_\ast \sqrt{\frac{R_\ast}{2a_p}}$$
在我们的例子中,代入
L太阳 = 3.83 x 1026
ap = 1.5 ∗ 1011 以及
A = 0.3
将得到 $T_{地球} = 255K$。实际计算非常复杂,包括云物理学。我们太阳系中的宜居带位于0.9 AU到1.7 AU之间。
由于气压降低,太阳的光度随时间增加。它开始燃烧氢时,亮度要暗30%。这将导致宜居带远离太阳。由于地球位于宜居带的内边缘附近,也许有一天它会移出这个区域!
持续宜居带
简而言之,它被称为CHZ,可以定义为在恒星整个主序星生命周期中液态水可以存在的区域。KST已经探测到许多确实位于宜居带的系外行星。
生物特征是任何物质——例如元素、同位素、分子或现象,它提供过去或现在生命的科学证据。一个例子是在一颗行星上同时探测到O2和CO2,这通常仅靠地质过程是无法实现的。这种探测是通过分析吸收光谱完成的。
要点
视向速度法、凌星法、引力微透镜法、成像法、天体测量法等技术已被用于探测系外行星。
视向速度法更容易偏向于探测具有更大周期的巨型行星。
热巨行星被称为“热木星”,较小质量行星被称为“热超级地球”。
宇宙中行星的数量超过宇宙中恒星的数量。
宜居带可以定义为恒星周围水可以以液态形式存在的一个区域。