哈勃参数与比例因子

本章将讨论哈勃参数和比例因子。

哈勃常数与比例因子的分数变化率

在本节中，我们将哈勃常数与比例因子的分数变化率联系起来。

我们可以用以下方式写出速度并简化。

$$v = \frac{\mathrm{d} r_p}{\mathrm{d} t}$$

$$= \frac{d[a(t)r_c]}{dt}$$

$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast (ar_c)$$

$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast r_p$$

这里，v是退行速度，a是比例因子，r_p是星系间的固有距离。

哈勃经验公式的形式为：

$$v = H \ast r_p$$

因此，比较上述两个方程，我们得到：

哈勃参数 = 比例因子的分数变化率

$$H = \frac{da}{dt} \ast \frac{1}{a}$$

注意 - 这不是一个常数，因为比例因子是时间的函数。因此它被称为哈勃参数而不是哈勃常数。

经验上我们写成：

$$H = \frac{V}{D}$$

因此，从这个方程中，我们可以推断，由于D在增加而V是一个常数，那么H随着时间的推移和宇宙的膨胀而减小。

在本节中，我们将了解如何结合罗伯逊-沃克模型使用弗里德曼方程。为了理解这一点，让我们以以下图像为例，该图像中有一个距离为r_p的测试质量，距离质量为M的天体。

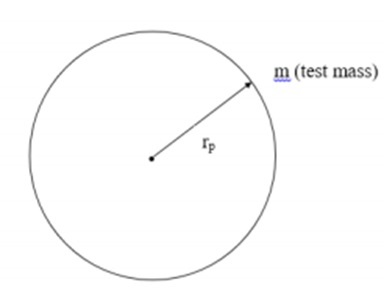
考虑到上图，我们可以将力表示为：

$$F = G \ast M \ast \frac{m}{r^2_p}$$

这里，G是万有引力常数，ρ是可观测宇宙内的物质密度。

现在，假设球体内质量密度均匀，我们可以写成：

$$M = \frac{4}{3} \ast \pi \ast r_p^3 \ast \rho$$

将这些代入我们的力方程，我们得到：

$$F = \frac{4}{3} \ast \pi \ast G \ast r_p \ast \rho \ast m$$

因此，我们可以将质量m的势能和动能写成：

$$V = -\frac{4}{3} \ast \pi \ast G \ast r^2_p \ast m \ast \rho$$

$$K.E = \frac{1}{2} \ast m \ast \frac{\mathrm{d} r_p^2}{\mathrm{d} t}$$

使用维里定理：

$$U = K.E + V$$

$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} r_p}{\mathrm{d} t} \right )^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$

但是这里，$r_p = ar_c$。所以我们得到：

$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} a}{\mathrm{d} t} \right )^2 r_c^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$

进一步简化后，我们得到弗里德曼方程：

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi}{3} \ast G \ast \rho + \frac{2U}{m} \ast r_c^2 \ast a^2$$

这里U是一个常数。我们还注意到，我们目前生活的宇宙是由物质主导的，而辐射能量密度非常低。

打印页面