红移和后退速度

---

---

哈勃的观测利用了径向速度与谱线位移相关的事实。在这里，我们将观察四种情况，并找到后退速度（$v_r$）和红移 (z) 之间的关系。

情况一：源运动的非相对论性情况

在这种情况下，v远小于c。光源发出某种信号（声音、光等），该信号以波阵面的形式传播。在源参考系中，两个连续信号发送之间的时间间隔为Δts。在观察者参考系中，两个连续信号接收之间的时间间隔为Δto。

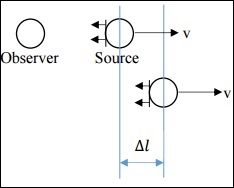
如果观察者和光源都是静止的，则Δts = Δto，但这里并非如此。相反，关系如下。

$$\Delta t_o = \Delta t_s + \frac{\Delta l}{c}$$

现在，$\Delta l = v \Delta t_s$

此外，由于（波速×时间）=波长，我们得到

$$\frac{\Delta t_o}{\Delta t_s} = \frac{\lambda_o}{\lambda_s}$$

根据上述方程式，我们得到以下关系：

$$\frac{\lambda_o}{\lambda_s} = 1 + \frac{v}{c}$$

其中$\lambda _s$是光源处信号的波长，$\lambda _o$是观察者解释的信号波长。

在这里，由于光源正在远离观察者，因此v为正。

红移：

$$z = \frac{\lambda_o - \lambda_s}{\lambda_s} = \frac{\lambda_o}{\lambda_s} - 1$$

根据上述方程式，我们得到红移如下。

$$z = \frac{v}{c}$$

情况二：观察者运动的非相对论性情况

在这种情况下，v远小于c。这里，Δl不同。

$$\Delta l = v \Delta t_o$$

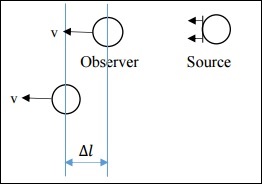
简化后，我们得到：

$$\frac{\Delta t_o}{\Delta t_s} = \left ( 1 - \frac{v}{c} \right )^{-1}$$

我们得到红移如下：

$$z = \frac{v/c}{1-v/c}$$

由于v << c，情况一和情况二的红移表达式近似相同。

让我们看看上面两种情况下获得的红移有何不同。

$$z_{II} - z_I = \frac{v}{c} \left [ \frac{1}{1 - v/c}-1 \right ]$$

因此，由于$(v/c)^2$因子，$z_{II} − z_{I}$是一个非常小的数字。

这意味着，如果v << c，我们无法判断光源是运动的还是静止的。

现在让我们了解狭义相对论基础(Special Theory of Relativity)：

• 光速是一个常数。

• 当光源（或观察者）以与光速相当的速度运动时，会观察到相对论效应。

• 时间膨胀：$\Delta t_o = \gamma \Delta t_s$

• 长度收缩：$\Delta l_o = \Delta t_s/\gamma$

• 这里，$\gamma$是洛伦兹因子，大于1。

$$\gamma = \frac{1}{\sqrt{1-(v^2/c^2)}}$$

情况三：光源运动的相对论性情况

在这种情况下，v与c相当。参考与情况一相同的图形。由于相对论效应，观察到时间膨胀，因此获得以下关系。（光源以相对论速度运动）

$$\Delta t_o = \gamma \Delta t_s + \frac{\Delta l}{c}$$

$$\Delta l = \frac{v\gamma \Delta t_s}{c}$$

$$\frac{\Delta t_o}{\Delta t_s} = \frac{1 + v/c}{\sqrt{1- (v^2/c^2)}}$$

进一步简化后，我们得到：

$$1 + z = \sqrt{\frac{1+v/c}{1-v/c}}$$

上述表达式称为运动多普勒频移表达式。

情况四：观察者运动的相对论性情况

参考与情况二相同的图形。由于相对论效应，观察到时间缩短，因此获得以下关系。（观察者以相对论速度运动）

$$\Delta t_o = \frac{\Delta t_s}{\gamma}+\frac{\Delta l}{c}$$

$$\Delta l = \frac{v\Delta t_o}{c}$$

$$\frac{\Delta t_o}{\Delta t_s} = \frac{\sqrt{1-( v^2/c^2)}}{1-v/c}$$

进一步简化后，我们得到：

$$1 + z = \sqrt{\frac{1+ v/c}{1- v/c}}$$

上述表达式与我们在情况三中得到的结果相同。

要点

• 恒星的后退速度和红移是相关的量。

• 在非相对论性情况下，我们无法确定光源是运动的还是静止的。

• 在相对论性情况下，光源或观察者运动的红移-后退速度关系没有区别。

• 运动的钟走得慢，是相对论的直接结果。