宇宙学度规与膨胀

根据能量守恒定律和质量守恒定律，包括质量在内的总能量 (E=mc²) 在宇宙中任何过程的每一步都保持不变。宇宙的膨胀本身会消耗能量，这可能来自光子波长的拉伸（宇宙红移）、暗能量相互作用等。

为了加快对超过26,000个星系的调查，Stephen A. Shectman设计了一种能够同时测量112个星系的仪器。在一个金属板上，钻出了与天空星系位置对应的孔。光纤电缆将每个星系的光传输到位于智利拉斯坎帕纳斯天文台2.5米杜邦望远镜上的光谱仪上的独立通道。

为了达到最大效率，使用了被称为漂移扫描测光法的专业技术，其中望远镜指向调查区域的起点，然后关闭自动驱动。望远镜静止不动，天空漂移而过。计算机以与地球自转相同的速率读取CCD探测器的信息，产生一个在恒定天球纬度上长时间连续的图像。测光总共花费了450小时。

存在不同形式的噪声，其数学建模取决于其特性而不同。各种物理过程在大尺度上演化了宇宙的功率谱。由于量子涨落而赋予的初始功率谱遵循频率的负三次幂，这是一种三维的粉红噪声谱。

度规

在宇宙学中，首先必须对空间有一个定义。度规是描述空间中点的数学表达式。对天空的观测是在球面几何中进行的；因此，将使用球坐标系。两个紧密间隔的点之间的距离由下式给出：

$$ds^2 = dr^2 + r^2\theta ^2 + r^2 sin^2\theta d\phi^2$$

下图显示了三维非膨胀欧几里得空间中的几何形状。

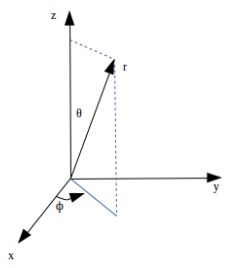
该几何形状仍然在三维非膨胀欧几里得空间中。因此，定义框架本身的参考网格将是膨胀的。下图描述了增强的度规。

将比例因子放入非膨胀空间的方程中，称为“比例因子”，它结合了宇宙相对于时间的膨胀。

$$ds^2 = a^2(t)\left [ dr^2 + r^2\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$$

其中a(t)是比例因子，有时写成R(t)。而a(t) > 1表示度规的放大，a(t) < 1表示度规的缩小，a(t) = 1表示度规恒定。按照惯例，a(t₀) = 1。

在共同移动坐标系中，测量尺度与框架（膨胀宇宙）一起膨胀。

这里，$\left [ dr^2 + r^2\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$是共同移动距离，$ds^2$是固有距离。

固有距离将对应于在观测时刻测量的从地球到遥远星系的实际距离，即物体的瞬时距离。

这是因为光子从遥远光源到达观察者时所走的距离将在观察者的$t=t_0$时刻接收，这意味着观察到的瞬时距离将是固有距离，并且可以使用速率因子和初始测量长度作为参考来预测未来的距离。

共同移动距离和固有距离的概念对于测量观测空间给定体积中星系实际数量密度值非常重要。必须使用共同移动距离来计算观测光子发射时星系的密度。一旦可以估计宇宙的膨胀速率，就可以获得该密度。

为了估计膨胀速率，可以观察长时间内观测到的遥远星系的距离变化。

打印页面