宇宙学 - 罗伯逊-沃克度规

---

---

在本章中，我们将详细了解罗伯逊-沃克度规。

尺度因子随时间变化的模型

假设一个光子从一个遥远的星系发射出来。空间在所有方向上对光子都是前进的。宇宙的膨胀是向所有方向进行的。让我们看看尺度因子在以下步骤中是如何随时间变化的。

步骤1 - 对于一个静态宇宙，尺度因子为1，即共动距离的值是物体之间的距离。

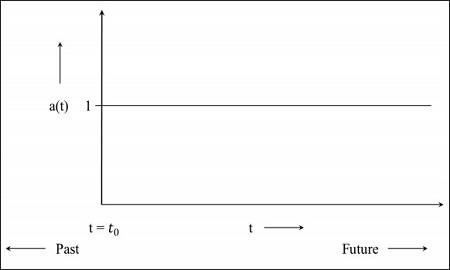
步骤2 - 下图是宇宙仍在膨胀但膨胀速度正在减小的图像，这意味着该图将从过去开始。t = 0表示宇宙从该点开始。

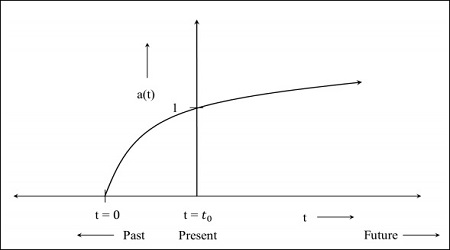
步骤3 - 下图是宇宙以更快的速度膨胀的图像。

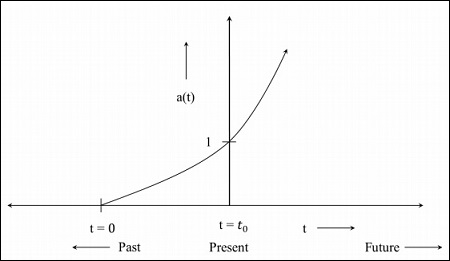
步骤4 - 下图是宇宙从现在开始收缩的图像。

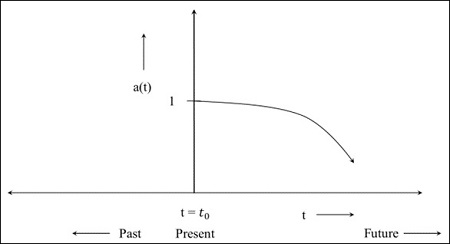
如果尺度因子的值在宇宙收缩过程中变为0，则意味着物体之间的距离变为0，即固有距离变为0。共动距离是现在宇宙中物体之间的距离，是一个常数。在未来，当尺度因子变为0时，所有东西都会靠拢。模型取决于宇宙的成分。

平坦（欧几里得：没有曲率参数）膨胀宇宙的度规表示为 -

$$ds^2 = a^2(t)\left ( dr^2+r^2d\theta^2+r^2sin^2\theta d\varphi^2 \right )$$

对于时空，我们在上述方程中得到的线元被修改为 -

$$ds^2 = c^2dt^2 - \left \{ a^2(t) \left ( dr^2 + r^2d\theta ^2 + r^2sin^2\theta d\varphi^2 \right ) \right \}$$

对于时空，光子发射和探测的时间是不同的。固有距离是物体瞬时的距离，由于宇宙膨胀，它会随着时间而变化。它是光子从不同的物体传播到我们这里所经过的距离。它与共动距离的关系为 -

$$d_p = a(t) \times d_c$$

其中$d_p$是固有距离，$d_c$是共动距离，它是固定的。

在现在宇宙中测量的物体距离被视为共动距离，这意味着共动距离是固定的，不受膨胀的影响。在过去，尺度因子小于1，这表明固有距离更小。

我们可以测量到星系的红移。因此，固有距离$d_p$对应于$c \times t(z)$，其中$t(z)$是朝向红移的回溯时间，c是真空中光速。回溯时间是红移(z)的函数。

基于上述概念，让我们分析一下宇宙学红移在这种$d_p = a(t) \times d_c$的场景中是如何解释的。

假设一个光子（它是地球束缚的）由星系G发射。$t_{em}$对应于光子发射的时间；$a(t_{em})$是光子发射时当时的尺度因子。到光子被探测到时，整个宇宙已经膨胀了，即光子在探测时发生了红移。$t_{obs}$对应于光子被探测到的时间，相应的尺度因子是$a(t_{obs})$。

宇宙增长了多少倍由以下公式给出 -

$$\frac{a(t_{obs})}{a(t_{em})}$$

波长扩展了多少倍为 -

$$\frac{\lambda_{obs}}{\lambda_{em}}$$

这等于宇宙增长了多少倍。符号具有其通常的含义。因此，

$$\frac{a(t_{obs})}{a(t_{em})} = \frac{\lambda_{obs}}{\lambda_{em}}$$

我们知道红移(z)为 -

$$z=\frac{\lambda_{obs} - \lambda_{em}}{\lambda_{em}} = \frac{\lambda_{obs}}{\lambda_{em}} - 1$$

$$1 + z = \frac{a(t_{obs})}{a(t_{em})}$$

尺度因子的当前值为1，因此$a(t_{obs}) = 1$，并将过去光子发射时的尺度因子表示为$a(t)$。

因此，

$$1 + z = \frac{1}{a(t)}$$

宇宙学红移的解释

为了理解这一点，让我们举个例子：如果$z = 2$，那么$a(t) = 1/3$。

这意味着自光线离开该物体以来，宇宙已经膨胀了三倍。接收到的辐射的波长膨胀了三倍，因为在从发射物体传播的过程中，空间膨胀了相同的倍数。需要注意的是，在如此大的z值下，红移主要是宇宙学红移，它不是物体相对于我们的实际退行速度的有效度量。

对于宇宙微波背景辐射（CMB），z = 1089，这意味着现在的宇宙已经膨胀了∼1090倍。平坦、欧几里得、膨胀宇宙的度规表示为 -

$$ds^2 = a^2(t)(dr^2 + r^2d\theta^2 + r^2sin^2\theta d\varphi^2)$$

我们希望在任何曲率下写出度规。

罗伯逊和沃克证明了对于任何曲率宇宙（它是均匀且各向同性的），度规表示为 -

$$ds^2 = a^2(t) \left [ \frac{dr^2}{1-kr^2} + r^2d\theta^2 + r^2sin^2\theta d\varphi^2 \right ]$$

这通常被称为罗伯逊-沃克度规，对于任何空间拓扑都成立。请注意$dr^2$中的额外因子。这里𝑘是曲率常数。

宇宙的几何形状

宇宙的几何形状借助以下曲率来解释，包括 -

• 正曲率
• 负曲率
• 零曲率

让我们详细了解一下这些。

正曲率

如果在曲率表面上的任意一点处画出的切平面在曲率表面上不与任何点相交，则称其为具有正曲率的曲面，即曲面位于该点切平面的同一侧。球体的表面具有正曲率。

负曲率

如果在曲率表面上的某一点处画出的切平面与曲率表面上的任意点相交，则称其为具有负曲率的曲面，即曲面在两个不同的方向上远离切平面弯曲。马鞍形的表面具有负曲率。

现在考虑球体的表面。如果通过连接三个点用测地线（大圆的弧）在球体的表面上构造一个三角形，则球面三角形的内角和大于180^o，即 -

$$\alpha + \beta + \gamma > \pi$$

这样的空间称为正曲率空间。此外，曲率是均匀且各向同性的。一般来说，球面三角形顶点的角度遵循以下关系 -

$$\alpha + \beta +\gamma = \pi + A/R^2$$

其中A是三角形的面积，R是球体的半径。下图描绘了一个正曲率空间。

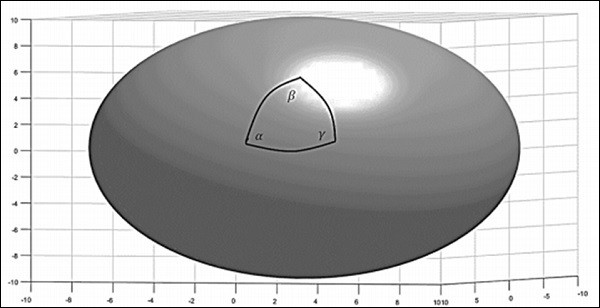
对于正曲率，平行线应该相交。考虑地球的表面，它是一个正曲率空间。在赤道上取两个起点。垂直穿过赤道的线称为经线。由于这些线垂直穿过赤道，因此可以将它们称为平行线。从赤道开始，它们最终会在两极相交。这种方法被卡尔·弗里德里希·高斯等人用来理解地球的拓扑结构。

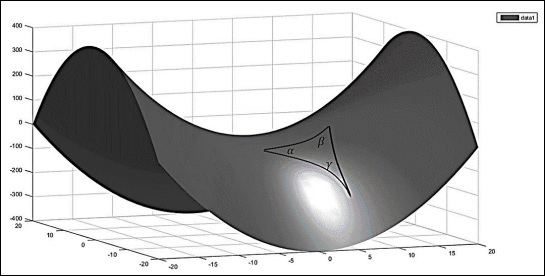
考虑一个负曲率空间（下图所示的马鞍），三角形的内角和小于180^o，即 -

$$\alpha + \beta + \gamma < \pi$$

顶点的角度遵循以下关系 -

$$\alpha + \beta + \gamma = \pi - A/R^2$$

零曲率

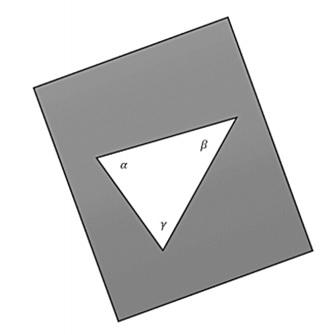
平面表面具有零曲率。现在对于一个平面空间，如果取一个平面，并通过连接三个点用测地线（直线）构造一个三角形，则内角和将为 -

$$\alpha + \beta + \gamma = \pi$$

下图是一个平坦的二维空间。

如果想要一个空间是均匀且各向同性的，则只有三种可能性：空间可以是均匀平坦的，或者可以具有均匀的正曲率，或者可以具有均匀的负曲率。

曲率常数可以取以下三个值中的任何一个。

$$k = \begin{cases}+1, & for \: a\: positively \: curved\: space;\\\quad 0, & for\: a \: flat \: space;\\-1, & for\: a \: negatively \: curved \: space;\end{cases}$$

宇宙的全局拓扑

宇宙具有一定的拓扑结构，但在局部可能存在皱褶。根据物质在空间中的分布情况，曲率存在较小的变化。假设存在一类物体，无论其在宇宙中的哪个位置，其真实尺寸都相同，这意味着它们就像标准烛光一样。它们的亮度不同，但尺寸相同。

如果物体位于正曲率空间中，并且光子来自点A（物体的一端）和点B（物体的另一端），那么光子将在正曲率空间中沿测地线路径平行传播，并最终相遇。对于C处的观察者来说，它似乎来自不同方向的两个不同点。

如果物体位于局部宇宙中，我们测量角尺寸，它不受曲率的影响。如果在更大的红移处观察同一类物体，则角尺寸与其不相关。

$$\theta = \frac{d}{r}$$

其中d是物体的尺寸，r是到物体的距离，即如果尺寸大于局部尺寸，则意味着曲率为正。下图是正曲率空间中检测到的光子的示意图。

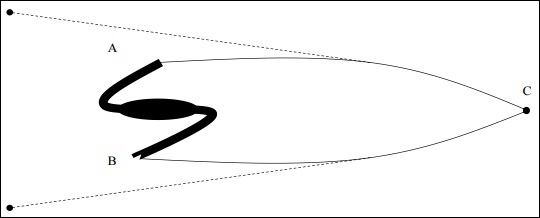
需要注意的是，不存在真正具有标准尺寸和形态的天体物理物体。虽然人们认为巨大的椭圆cD星系符合标准烛光的条件，但后来发现它们也会随着时间演化。

测量星系距离

在本节中，我们将讨论如何通过考虑下图来测量星系的距离。

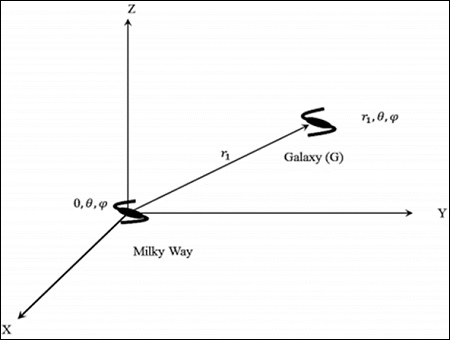
考虑在宇宙静止参考系中位于(r, θ,)的银河系。可以通过假设宇宙的均匀性，将𝑟取为0；(0, θ,ϕ)，即宇宙的中心。

考虑位于(r1, θ,)的星系“G”。距离（本征距离）是光子传播的最短径向距离。根据时空的对称性，从r = 0到r = r1的零测地线在空间中具有恒定的方向。在其径向传播过程中，角坐标不会改变。如果角坐标发生改变，则它不是最短路径。这就是为什么dr²中存在曲率项的原因。

要点回顾

• 宇宙的膨胀是向所有方向进行的。

• 宇宙可以是静态的、膨胀的或收缩的，具体取决于尺度因子的演化。

• cD星系会随着时间演化，因此不能用作标准烛光。

• 宇宙具有一定的拓扑结构，但在局部可能存在皱褶。