Python math.hypot() 方法

---

---

Python 的 math.hypot() 方法用于计算直角三角形的斜边长度。

在 Python 3.8 之前的版本中，此方法仅用于查找直角三角形的斜边长度；但在 Python 3.8 及之后的版本中，它也用于查找欧几里得范数。

欧几里得范数定义为笛卡尔平面上原点与坐标之间的距离。因此，它实际上就是斜边，其中坐标轴充当直角三角形的底边和高。

为了更好地理解这一点，让我们来看下面的图示 -

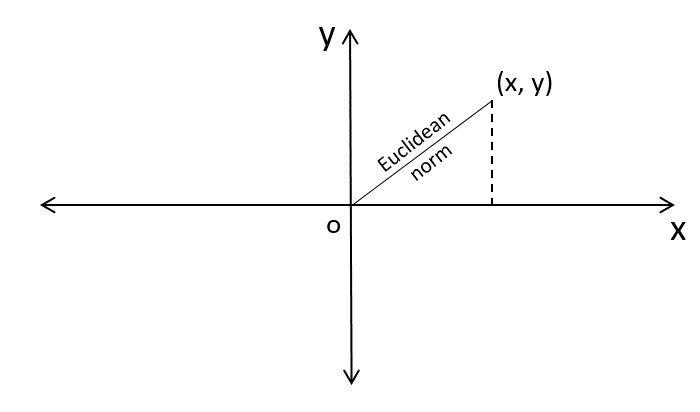
注意 - 此函数不能直接访问，因此我们需要导入 math 模块，然后需要使用 math 静态对象调用此函数。

语法

以下是 Python math.hypot() 方法的语法 -

math.hypot(x, y)

参数

• x, y - 必须是数值。

返回值

此方法返回欧几里得范数，sqrt(x*x + y*y)。

示例

以下示例演示了 Python math.hypot() 方法的用法。这里，我们创建两个包含正浮点值的数字对象。这些对象作为参数传递给此方法，并计算欧几里得范数。

import math # This will import the math module

# Create two numeric objects
x = 12.98
y = 44.06

# Calculate the euclidean norm
hyp = math.hypot(x, y)

# Display the length of the euclidean norm
print("The length of Euclidean norm is:", hyp)

运行以上程序时，会产生以下结果 -

The length of Euclidean norm is: 45.93216737755797

示例

即使我们将负坐标 x 和 y 作为参数传递给此方法，欧几里得范数也会作为正值获得（因为它是距离）。

在以下示例中，我们创建两个包含负值的数字对象。这些对象作为参数传递给该方法，并计算欧几里得范数的长度。

import math # This will import the math module

# Create two numeric objects with negative values
x = -10.66
y = -15.12

# Calculate the euclidean norm
hyp = math.hypot(x, y)

# Display the length of the euclidean norm
print("The length of Euclidean norm is:", hyp)

让我们编译并运行给定的程序，输出如下 -

The length of Euclidean norm is: 18.5

示例

假设 x 和 y 坐标分别作为正无穷大和负无穷大值传递，欧几里得范数的长度将是正无穷大。

import math # This will import the math module

# Create two numeric objects with infinity
x = float("inf")
y = float("-inf")

# Calculate the Euclidean norm
hyp = math.hypot(x, y)

# Display the length of the Euclidean norm
print("The length of Euclidean norm is:", hyp)

执行上面的程序后，输出如下 -

The length of Euclidean norm is: inf

示例

当我们将NaN值作为参数传递给此方法时，返回值也将是NaN值。

import math # This will import the math module

# Create two numeric objects with NaN values
x = float("nan")
y = float("nan")

# Calculate the euclidean norm
hyp = math.hypot(x, y)

# Display the length of the euclidean norm
print("The length of Euclidean norm is:", hyp)

编译并运行程序，结果如下：

The length of Euclidean norm is: nan