Python中的随机游走实现

---

---

随机游走是一个每一步都随机确定的过程，通常用于模拟不可预测的运动。它用于描述由一系列随机移动组成的路径。

简单的随机游走可以是一维的，其中粒子必须向左或向右移动，没有任何偏向。关于随机游走应用于更高维度（如二维、三维和四维）的概念，运动是在特定维度中随机方向进行的。

每个额外的维度都会增加游走的难度，并提供更多关于随机过程和空间搜索的信息。这些理论包含了Python代码，用于一维、二维、三维和四维随机游走，以解释如何用计算机图形模拟它们。

所需库的安装

1. NumPy

用于Python数值计算的NumPy库，用于处理数组和执行数学运算。

语法

pip install numpy

2. Matplotlib

Matplotlib是一个绘图库，用于在Python中创建静态、动画和交互式可视化。

语法

pip install matplotlib

一维随机游走的实现

以下代码用于在Python中实现一维随机游走：

import numpy as np
import matplotlib.pyplot as plt

def random_walk_1d(steps):
   """Generate a 1D random walk."""
   walk = np.zeros(steps)
   for i in range(1, steps):
      step = np.random.choice([-1, 1])
      walk[i] = walk[i - 1] + step
   return walk

# Number of steps
steps = 1000
walk = random_walk_1d(steps)

# Plot the random walk
plt.figure(figsize=(10, 6))
plt.plot(walk, label='1D Random Walk')
plt.xlabel('Steps')
plt.ylabel('Position')
plt.title('1D Random Walk')
plt.legend()
plt.show()

输出

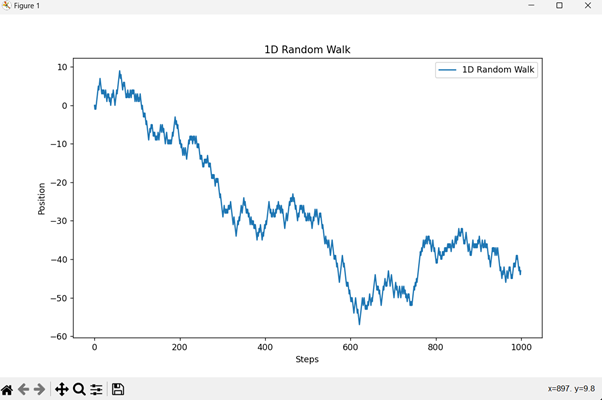
代码解释

• **导入** - numpy用于数值运算。matplotlib.pyplot用于绘制游走。**random_walk_1d**
• **函数** - 创建一维随机游走。
  对于每一步，随机决定向左移动(-1)还是向右移动(+1)。
  累加这些步数以计算每一步的位置。
• **绘图** - 绘制位置与步数的关系图，以便可视化随机游走。

二维随机游走的实现

以下代码用于在Python中实现二维随机游走：

import numpy as np
import matplotlib.pyplot as plt

def random_walk_2d(steps):
   """Generate a 2D random walk."""
   positions = np.zeros((steps, 2))
   for i in range(1, steps):
      step = np.random.choice(['up', 'down', 'left', 'right'])
      if step == 'up':
         positions[i] = positions[i - 1] + [0, 1]
      elif step == 'down':
         positions[i] = positions[i - 1] + [0, -1]
      elif step == 'left':
         positions[i] = positions[i - 1] + [-1, 0]
      elif step == 'right':
         positions[i] = positions[i - 1] + [1, 0]
   return positions

# Number of steps
steps = 1000
positions = random_walk_2d(steps)

# Plot the random walk
plt.figure(figsize=(10, 10))
plt.plot(positions[:, 0], positions[:, 1], label='2D Random Walk')
plt.xlabel('X Position')
plt.ylabel('Y Position')
plt.title('2D Random Walk')
plt.legend()
plt.grid(True)
plt.show()

输出

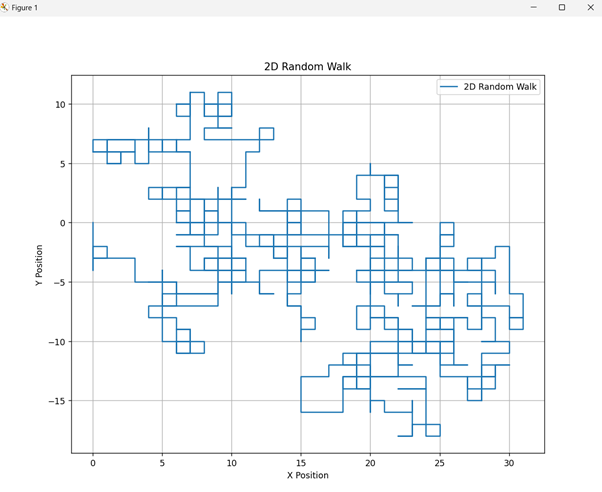
代码解释

**向四个方向之一移动** - 向上、向下、向左或向右。相应地更新位置并记录每一步。

三维随机游走的实现

以下代码用于在Python中实现三维随机游走：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def random_walk_3d(steps):
   """Generate a 3D random walk."""
   positions = np.zeros((steps, 3))
   for i in range(1, steps):
      step = np.random.choice(['x+', 'x-', 'y+', 'y-', 'z+', 'z-'])
      if step == 'x+':
         positions[i] = positions[i - 1] + [1, 0, 0]
      elif step == 'x-':
         positions[i] = positions[i - 1] + [-1, 0, 0]
      elif step == 'y+':
         positions[i] = positions[i - 1] + [0, 1, 0]
      elif step == 'y-':
         positions[i] = positions[i - 1] + [0, -1, 0]
      elif step == 'z+':
         positions[i] = positions[i - 1] + [0, 0, 1]
      elif step == 'z-':
         positions[i] = positions[i - 1] + [0, 0, -1]
   return positions

# Number of steps
steps = 1000
positions = random_walk_3d(steps)

# Plot the random walk
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
ax.plot(positions[:, 0], positions[:, 1], positions[:, 2], label='3D Random Walk')
ax.set_xlabel('X Position')
ax.set_ylabel('Y Position')
ax.set_zlabel('Z Position')
ax.set_title('3D Random Walk')
ax.legend()
plt.show()

输出

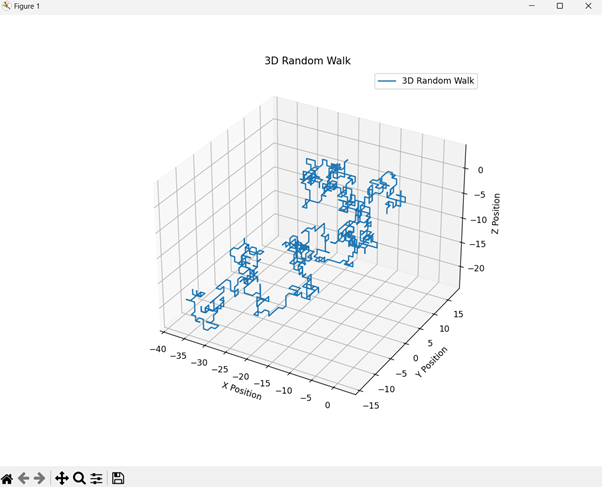
代码解释

• **向六个方向之一移动** - x+、x-、y+、y-、z+或z-。更新三维空间中的位置。
• **绘图** - 使用matplotlib绘制二维随机游走。使用mpl_toolkits.mplot3d进行三维可视化绘制三维随机游走。

四维随机游走的实现

以下代码用于在Python中实现四维随机游走：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def random_walk_4d(steps):
   """Generate a 4D random walk."""
   positions = np.zeros((steps, 4))
   for i in range(1, steps):
      direction = np.random.choice(['x+', 'x-', 'y+', 'y-', 'z+', 'z-', 'w+', 'w-'])
      if direction == 'x+':
         positions[i] = positions[i - 1] + [1, 0, 0, 0]
      elif direction == 'x-':
         positions[i] = positions[i - 1] + [-1, 0, 0, 0]
      elif direction == 'y+':
         positions[i] = positions[i - 1] + [0, 1, 0, 0]
      elif direction == 'y-':
         positions[i] = positions[i - 1] + [0, -1, 0, 0]
      elif direction == 'z+':
         positions[i] = positions[i - 1] + [0, 0, 1, 0]
      elif direction == 'z-':
         positions[i] = positions[i - 1] + [0, 0, -1, 0]
      elif direction == 'w+':
         positions[i] = positions[i - 1] + [0, 0, 0, 1]
      elif direction == 'w-':
         positions[i] = positions[i - 1] + [0, 0, 0, -1]
   return positions

# Number of steps
steps = 1000
positions = random_walk_4d(steps)

# Plot a 4D random walk by projecting onto 3D
fig = plt.figure(figsize=(10, 10))

# 3D projection using first three dimensions
ax1 = fig.add_subplot(121, projection='3d')
ax1.plot(positions[:, 0], positions[:, 1], positions[:, 2], label='Projection: X-Y-Z')
ax1.set_xlabel('X Position')
ax1.set_ylabel('Y Position')
ax1.set_zlabel('Z Position')
ax1.set_title('4D Random Walk (Projection)')
ax1.legend()

# Another 3D projection using last three dimensions
ax2 = fig.add_subplot(122, projection='3d')
ax2.plot(positions[:, 1], positions[:, 2], positions[:, 3], label='Projection: Y-Z-W')
ax2.set_xlabel('Y Position')
ax2.set_ylabel('Z Position')
ax2.set_zlabel('W Position')
ax2.set_title('4D Random Walk (Projection)')
ax2.legend()

plt.show()

输出

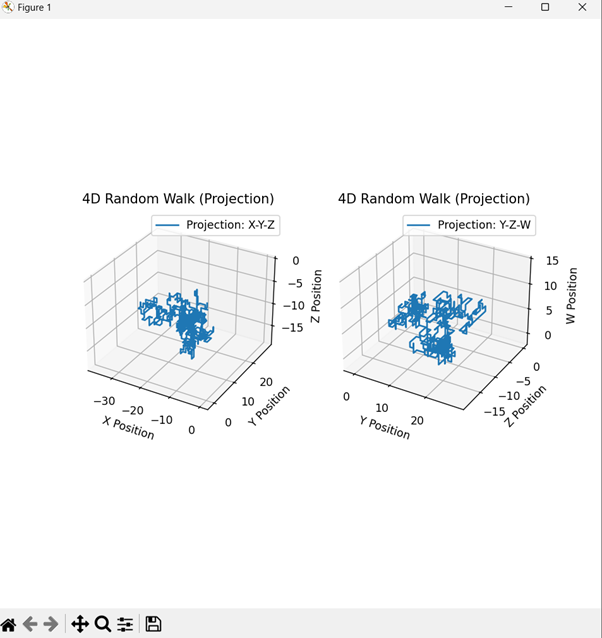
代码解释

• **random_walk_4d函数** - 向八个方向之一移动：x+、x-、y+、y-、z+、z-、w+、w-。更新四维空间中的位置。
• **绘图** - 由于四维数据太复杂而无法直接可视化，我们将其映射到三维空间，以便我们可以很好地可视化。第一个子图投影到X-Y-Z空间。第二个子图投影到Y-Z-W空间。
• **可视化** - 在这些三维投影中，游走的演变是清晰的——你可以从这里了解四维游走的行为。