控制系统 - 方框图代数

---

---

方框图代数只不过是方框图基本元素相关的代数运算。这种代数处理的是代数方程的图形表示。

方框的基本连接

两个方框之间有三种基本类型的连接。

串联连接

串联连接也称为级联连接。在下图中，两个具有传递函数$G_1(s)$和$G_2(s)$的方框串联连接。

对于这种组合，我们将得到输出$Y(s)$为

$$Y(s)=G_2(s)Z(s)$$

其中，$Z(s)=G_1(s)X(s)$

$$\Rightarrow Y(s)=G_2(s)[G_1(s)X(s)]=G_1(s)G_2(s)X(s)$$

$$\Rightarrow Y(s)=\lbrace G_1(s)G_2(s)\rbrace X(s)$$

将此方程与输出方程的标准形式$Y(s)=G(s)X(s)$进行比较。其中，$G(s) = G_1(s)G_2(s)$。

这意味着我们可以用一个方框表示两个方框的串联连接。这个单一方框的传递函数是这两个方框的传递函数的乘积。等效方框图如下所示。

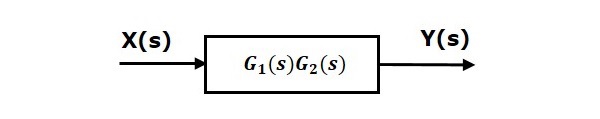
类似地，您可以用一个方框表示'n'个方框的串联连接。这个单一方框的传递函数是所有这'n'个方框的传递函数的乘积。

并联连接

并联连接的方框将具有相同的输入。在下图中，两个具有传递函数$G_1(s)$和$G_2(s)$的方框并联连接。这两个方框的输出连接到求和点。

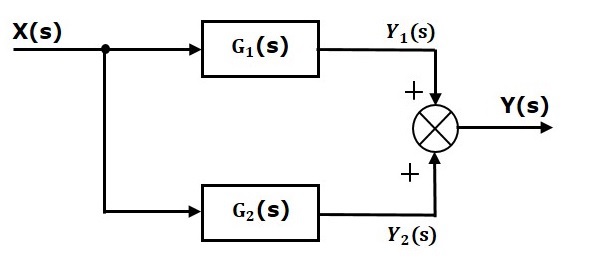
对于这种组合，我们将得到输出$Y(s)$为

$$Y(s)=Y_1(s)+Y_2(s)$$

其中，$Y_1(s)=G_1(s)X(s)$和$Y_2(s)=G_2(s)X(s)$

$$\Rightarrow Y(s)=G_1(s)X(s)+G_2(s)X(s)=\lbrace G_1(s)+G_2(s)\rbrace X(s)$$

将此方程与输出方程的标准形式$Y(s)=G(s)X(s)$进行比较。

其中，$G(s)=G_1(s)+G_2(s)$。

这意味着我们可以用一个方框表示两个方框的并联连接。这个单一方框的传递函数是这两个方框的传递函数的和。等效方框图如下所示。

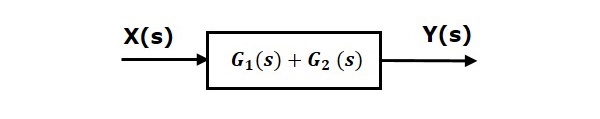
类似地，您可以用一个方框表示'n'个方框的并联连接。这个单一方框的传递函数是所有这'n'个方框的传递函数的代数和。

反馈连接

正如我们在前几章中讨论的那样，有两种类型的反馈——正反馈和负反馈。下图显示了负反馈控制系统。在这里，两个具有传递函数$G(s)$和$H(s)$的方框形成一个闭环。

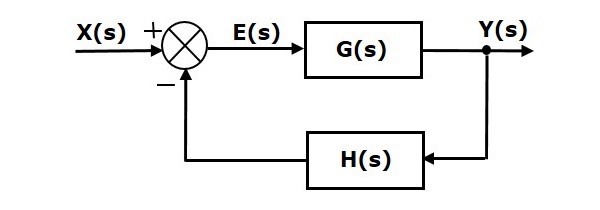
求和点的输出是：

$$E(s)=X(s)-H(s)Y(s)$$

输出$Y(s)$是：

$$Y(s)=E(s)G(s)$$

将$E(s)$的值代入上述方程。

$$Y(s)=\left \{ X(s)-H(s)Y(s)\rbrace G(s) \right\}$$

$$Y(s)\left \{ 1+G(s)H(s)\rbrace = X(s)G(s) \right\}$$

$$\Rightarrow \frac{Y(s)}{X(s)}=\frac{G(s)}{1+G(s)H(s)}$$

因此，负反馈闭环传递函数为$\frac{G(s)}{1+G(s)H(s)}$

这意味着我们可以用一个方框表示两个方框的负反馈连接。这个单一方框的传递函数是负反馈的闭环传递函数。等效方框图如下所示。

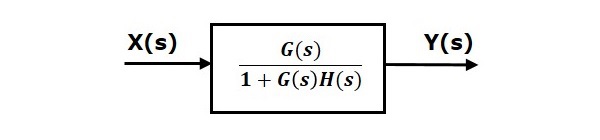
类似地，您可以用一个方框表示两个方框的正反馈连接。这个单一方框的传递函数是正反馈的闭环传递函数，即$\frac{G(s)}{1-G(s)H(s)}$

求和点的方框图代数

相对于方框，移动求和点有两种可能性：

• 将求和点移到方框之后
• 将求和点移到方框之前

现在让我们逐一看看上述两种情况下需要进行什么样的安排。

将求和点移到方框之后

考虑下图所示的方框图。在这里，求和点位于方框之前。

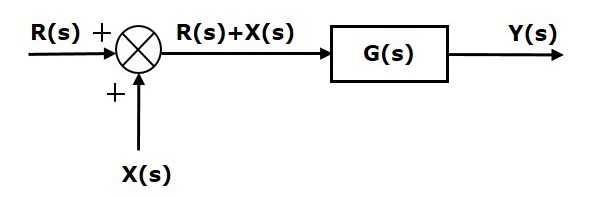
求和点有两个输入$R(s)$和$X(s)$。它的输出是$\left \{R(s)+X(s)\right\}$。

因此，方框$G(s)$的输入是$\left \{R(s)+X(s)\right \}$，其输出为：

$$Y(s)=G(s)\left \{R(s)+X(s)\right \}$$

$\Rightarrow Y(s)=G(s)R(s)+G(s)X(s)$ (公式1)

现在，将求和点移到方框之后。此方框图如下图所示。

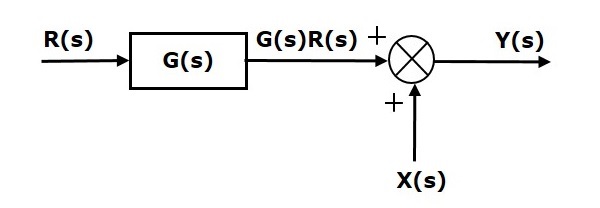
方框$G(s)$的输出是$G(s)R(s)$。

求和点的输出是

$Y(s)=G(s)R(s)+X(s)$ (公式2)

比较公式1和公式2。

第一项$‘G(s) R(s)’$在两个方程中都是相同的。但是，第二项有所不同。为了使第二项也相同，我们需要另一个方框$G(s)$。它具有输入$X(s)$，并且此方框的输出作为输入提供给求和点，而不是$X(s)$。此方框图如下图所示。

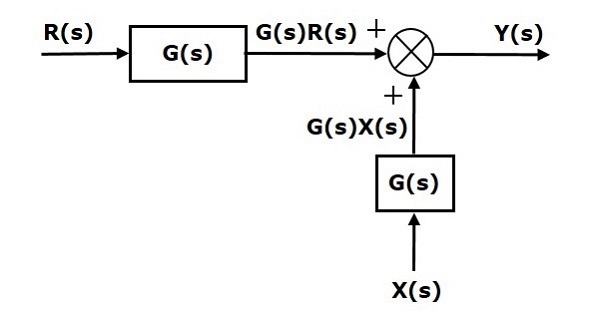
将求和点移到方框之前

考虑下图所示的方框图。在这里，求和点位于方框之后。

此方框图的输出为：

$Y(s)=G(s)R(s)+X(s)$ (公式3)

现在，将求和点移到方框之前。此方框图如下图所示。

此方框图的输出为：

$Y(S)=G(s)R(s)+G(s)X(s)$ (公式4)

比较公式3和公式4，

第一项$‘G(s) R(s)’$在两个方程中都是相同的。但是，第二项有所不同。为了使第二项也相同，我们需要另一个方框$\frac{1}{G(s)}$。它具有输入$X(s)$，并且此方框的输出作为输入提供给求和点，而不是$X(s)$。此方框图如下图所示。

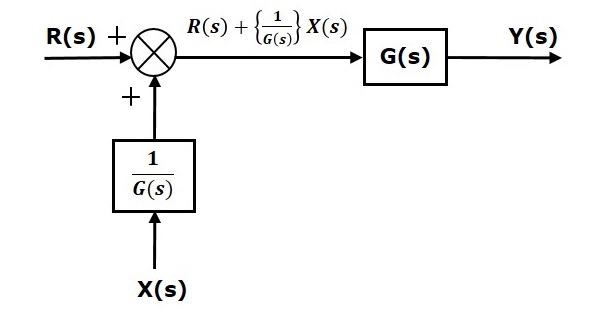
取样点的方框图代数

相对于方框，移动取样点有两种可能性：

• 将取样点移到方框之后
• 将取样点移到方框之前

现在让我们逐一看看上述两种情况下需要进行什么样的安排。

将取样点移到方框之后

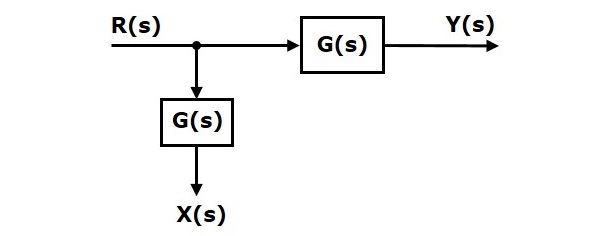
考虑下图所示的方框图。在这种情况下，取样点位于方框之前。

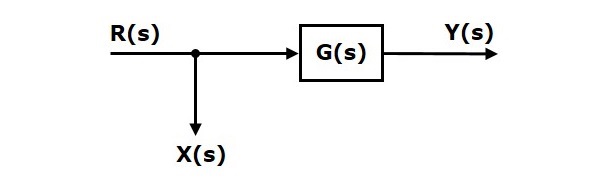
这里，$X(s)=R(s)$和$Y(s)=G(s)R(s)$

当您将取样点移到方框之后时，输出$Y(s)$将保持不变。但是，$X(s)$的值有所不同。因此，为了获得相同的$X(s)$值，我们需要另一个方框$\frac{1}{G(s)}$。它具有输入$Y(s)$，输出为$X(s)$。此方框图如下图所示。

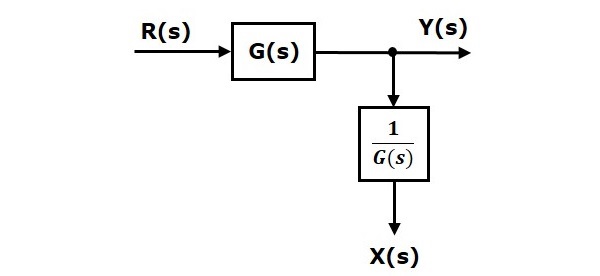
将取样点移到方框之前

考虑下图所示的方框图。在这里，取样点位于方框之后。

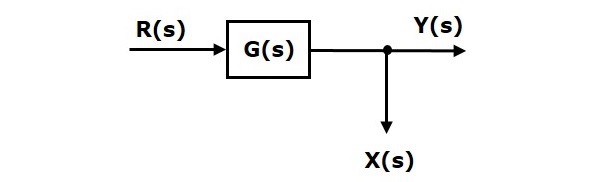
这里，$X(s)=Y(s)=G(s)R(s)$

当您将取样点移到方框之前时，输出$Y(s)$将保持不变。但是，$X(s)$的值有所不同。因此，为了获得相同的$X(s)$值，我们需要另一个方框$G(s)$。它具有输入$R(s)$，输出为$X(s)$。此方框图如下图所示。