控制系统 - 方块图化简

前面章节中讨论的概念有助于化简（简化）方块图。

方块图化简规则

遵循以下规则来简化（化简）包含许多方块、加法点和取样点的方块图。

• 规则 1 - 检查串联连接的方块并进行简化。

• 规则 2 - 检查并联连接的方块并进行简化。

• 规则 3 - 检查反馈回路中的方块并进行简化。

• 规则 4 - 如果在简化过程中取样点出现问题，将其向右移动。

• 规则 5 - 如果在简化过程中加法点出现问题，将其向左移动。

• 规则 6 - 重复上述步骤，直到得到简化形式，即单个方块。

注意 - 此单个方块中存在的传递函数是整个方块图的传递函数。

示例

考虑下图所示的方块图。让我们使用方块图化简规则来简化（化简）此方块图。

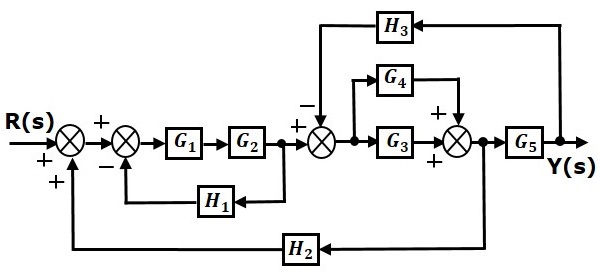
步骤 1 - 对方块 $G_1$ 和 $G_2$ 使用规则 1。对方块 $G_3$ 和 $G_4$ 使用规则 2。修改后的方块图如下所示。

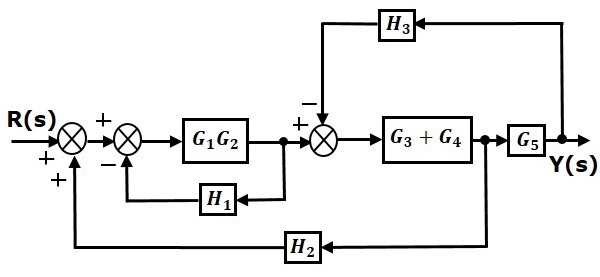
步骤 2 - 对方块 $G_1G_2$ 和 $H_1$ 使用规则 3。对方块 $G_5$ 后面的取样点使用规则 4 进行移动。修改后的方块图如下所示。

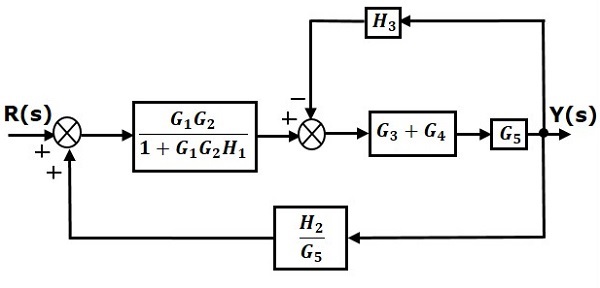
步骤 3 - 对方块 $(G_3 + G_4)$ 和 $G_5$ 使用规则 1。修改后的方块图如下所示。

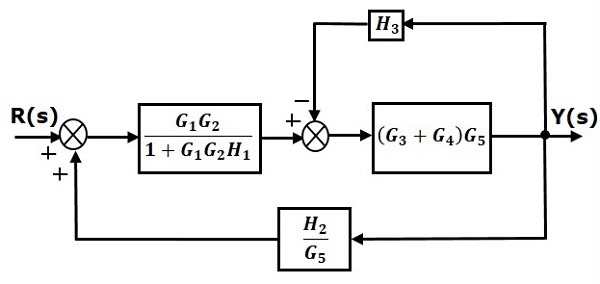
步骤 4 - 对方块 $(G_3 + G_4)G_5$ 和 $H_3$ 使用规则 3。修改后的方块图如下所示。

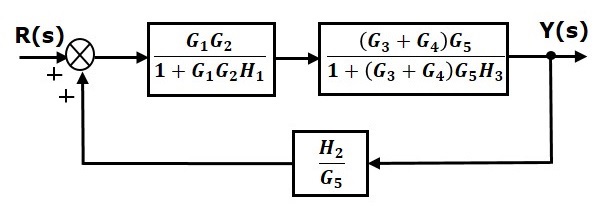
步骤 5 - 对串联连接的方块使用规则 1。修改后的方块图如下所示。

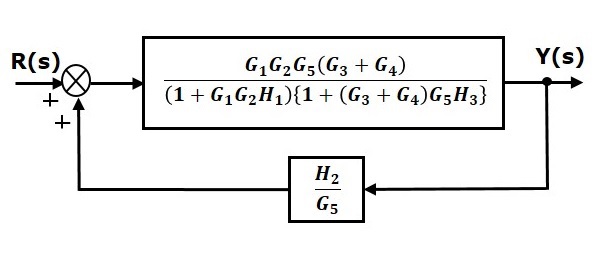
步骤 6 - 对反馈回路中的方块使用规则 3。修改后的方块图如下所示。这是简化的方块图。

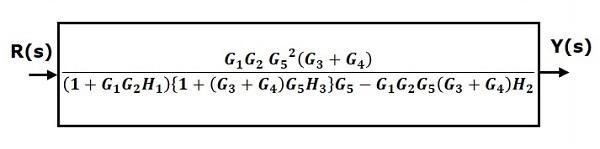
因此，系统的传递函数为

$$\frac{Y(s)}{R(s)}=\frac{G_1G_2G_5^2(G_3+G_4)}{(1+G_1G_2H_1)\lbrace 1+(G_3+G_4)G_5H_3\rbrace G_5-G_1G_2G_5(G_3+G_4)H_2}$$

注意 - 为了计算具有多个输入的方块图的传递函数，请按顺序执行以下步骤。

• 步骤 1 - 通过一次考虑一个输入并使其余输入为零来找到方块图的传递函数。

• 步骤 2 - 对其余输入重复步骤 1。

• 步骤 3 - 通过将所有这些传递函数相加来获得总的传递函数。

对于复杂的系统，方块图化简过程需要更多时间。因为，我们必须在每个步骤之后绘制（部分简化）的方块图。因此，为了克服这个缺点，可以使用信号流图（表示）。

在接下来的两章中，我们将讨论与信号流图相关的概念，即如何从给定的方块图中表示信号流图，以及仅使用增益公式而不进行任何化简过程即可计算传递函数。