控制系统 - 补偿器

---

---

补偿器有三种类型：滞后补偿器、超前补偿器和滞后-超前补偿器。这些是最常用的。

滞后补偿器

滞后补偿器是一种电网络，当施加正弦输入时，它会产生具有相位滞后的正弦输出。以下图显示了“s”域中的滞后补偿器电路。

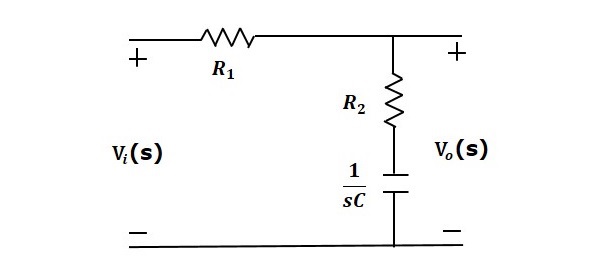
此处，电容与电阻R₂串联，输出电压在此组合上测量。

该滞后补偿器的传递函数为：

$$\frac{V_o(s)}{V_i(s)}=\frac{1}{\alpha} \left( \frac{s+\frac{1}{\tau}}{s+\frac{1}{\alpha\tau}} \right )$$

其中：

$$\tau=R_2C$$

$$\alpha=\frac{R_1+R_2}{R_2}$$

从上式可知，α总是大于1。

从传递函数可以看出，滞后补偿器在s = − 1/(ατ)处有一个极点，在s = −1/τ处有一个零点。这意味着在滞后补偿器的零极点配置中，极点更靠近原点。

将s = jω代入传递函数。

$$\frac{V_o(j\omega)}{V_i(j\omega)}=\frac{1}{\alpha}\left( \frac{j\omega+\frac{1}{\tau}}{j\omega+\frac{1}{\alpha\tau}}\right )$$

相角 φ = arctan(ωτ) − arctan(αωτ)

我们知道，输出正弦信号的相位等于输入正弦信号和传递函数的相位之和。

因此，为了在这个补偿器的输出端产生相位滞后，传递函数的相角应该为负。当α > 1时，就会发生这种情况。

超前补偿器

超前补偿器是一种电网络，当施加正弦输入时，它会产生具有相位超前的正弦输出。以下图显示了“s”域中的超前补偿器电路。

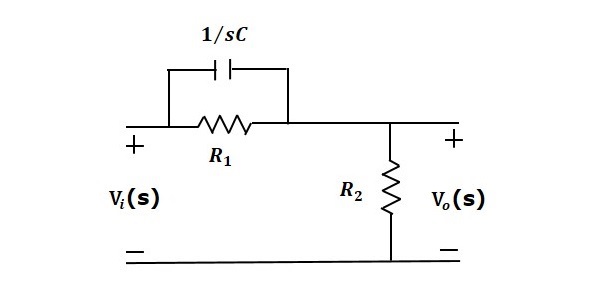
此处，电容与电阻R₁并联，输出电压在电阻R₂上测量。

该超前补偿器的传递函数为：

$$\frac{V_o(s)}{V_i(s)}=\beta \left( \frac{s\tau+1}{\beta s\tau+1} \right )$$

其中：

$$\tau=R_1C$$

$$\beta=\frac{R_2}{R_1+R_2}$$

从传递函数可以看出，超前补偿器在s = −1/β处有一个极点，在s = −1/(βτ)处有一个零点。

将s = jω代入传递函数。

$$\frac{V_o(j\omega)}{V_i(j\omega)}=\beta \left( \frac{j\omega\tau+1}{\beta j \omega\tau+1} \right )$$

相角 φ = arctan(ωτ) − arctan(βωτ)

我们知道，输出正弦信号的相位等于输入正弦信号和传递函数的相位之和。

因此，为了在这个补偿器的输出端产生相位超前，传递函数的相角应该为正。当0 < β < 1时，就会发生这种情况。因此，在超前补偿器的零极点配置中，零点更靠近原点。

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

滞后-超前补偿器

滞后-超前补偿器是一种电网络，在一个频率区域产生相位滞后，在另一个频率区域产生相位超前。它是滞后补偿器和超前补偿器的组合。以下图显示了“s”域中的滞后-超前补偿器电路。

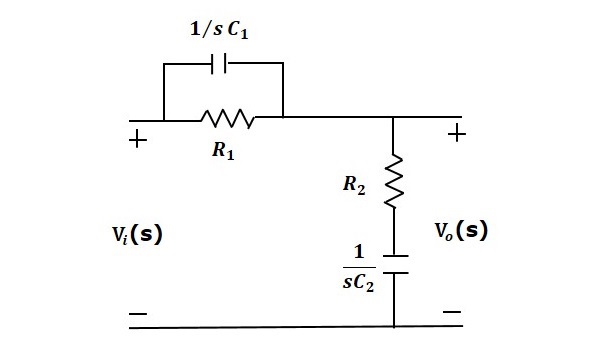
该电路看起来像是两个补偿器级联连接。因此，该电路的传递函数将是超前补偿器和滞后补偿器传递函数的乘积。

$$\frac{V_o(s)}{V_i(s)}=\beta \left( \frac{s\tau_1+1}{\beta s \tau_1+1} \right )\frac{1}{\alpha} \left ( \frac{s+\frac{1}{\tau_2}}{s+\frac{1}{\alpha\tau_2}} \right )$$

我们知道αβ=1。

$$\Rightarrow \frac{V_o(s)}{V_i(s)}=\left ( \frac{s+\frac{1}{\tau_1}}{s+\frac{1}{\beta\tau_1}} \right )\left ( \frac{s+\frac{1}{\tau_2}}{s+\frac{1}{\alpha\tau_2}} \right )$$

其中：

$$\tau_1=R_1C_1$$

$$\tau_2=R_2C_2$$