控制系统 - 稳定性

稳定性是一个重要的概念。在本章中，我们将讨论系统的稳定性和基于稳定性的系统类型。

什么是稳定性？

如果系统的输出处于控制之下，则称该系统是稳定的。否则，则称其为不稳定的。对于给定的有界输入，**稳定系统**产生有界输出。

下图显示了稳定系统的响应。

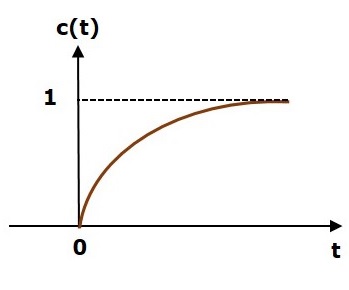
这是单位阶跃输入的一阶控制系统的响应。该响应的值介于 0 和 1 之间。因此，它是界输出。我们知道，单位阶跃信号对于所有正值t（包括零）的值都为 1。因此，它是界输入。因此，一阶控制系统是稳定的，因为输入和输出都是有界的。

基于稳定性的系统类型

我们可以根据稳定性将系统分类如下。

• 绝对稳定系统
• 条件稳定系统
• 临界稳定系统

绝对稳定系统

如果系统在所有系统组件值范围内都稳定，则称为**绝对稳定系统**。如果开环传递函数的所有极点都位于‘s’平面**的左半部分，则开环控制系统是绝对稳定的。类似地，如果闭环传递函数的所有极点都位于‘s’平面的左半部分，则闭环控制系统是绝对稳定的。