
- 控制系统教程
- 控制系统 - 首页
- 控制系统 - 简介
- 控制系统 - 反馈
- 数学模型
- 机械系统的建模
- 机械系统的电学类比
- 控制系统 - 方框图
- 方框图代数
- 方框图简化
- 信号流图
- 梅森增益公式
- 时间响应分析
- 一阶系统的响应
- 二阶系统的响应
- 时域指标
- 稳态误差
- 控制系统 - 稳定性
- 控制系统 - 稳定性分析
- 控制系统 - 根轨迹
- 根轨迹的绘制
- 频率响应分析
- 控制系统 - 波特图
- 波特图的绘制
- 控制系统 - 极坐标图
- 控制系统 - 奈奎斯特图
- 控制系统 - 补偿器
- 控制系统 - 控制器
- 控制系统 - 状态空间模型
- 状态空间分析
- 控制系统有用资源
- 控制系统 - 快速指南
- 控制系统 - 有用资源
- 控制系统 - 讨论
机械系统的电学类比
如果满足以下两个条件,则称两个系统为互为类比。
- 这两个系统在物理上是不同的
- 这两个系统的微分方程模型相同
电气系统和机械系统是两个物理上不同的系统。平移机械系统的电学类比有两种类型。分别是力-电压类比和力-电流类比。
力-电压类比
在力-电压类比中,将平移机械系统的数学方程与电气系统的网孔方程进行比较。
考虑以下所示的平移机械系统。
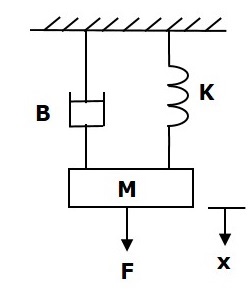
该系统的力平衡方程为
$$F=F_m+F_b+F_k$$
$\Rightarrow F=M\frac{\text{d}^2x}{\text{d}t^2}+B\frac{\text{d}x}{\text{d}t}+Kx$ (公式1)
考虑以下所示的电气系统。该电路由电阻器、电感器和电容器组成。所有这些元件都串联连接。施加到该电路的输入电压为$V$伏特,流过电路的电流为$i$安培。
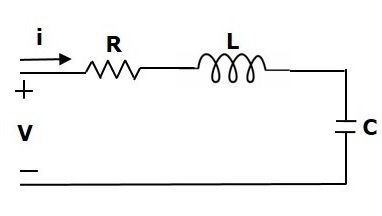
该电路的网孔方程为
$V=Ri+L\frac{\text{d}i}{\text{d}t}+\frac{1}{c}\int idt$ (公式2)
将$i=\frac{\text{d}q}{\text{d}t}$代入公式2。
$$V=R\frac{\text{d}q}{\text{d}t}+L\frac{\text{d}^2q}{\text{d}t^2}+\frac{q}{C}$$
$\Rightarrow V=L\frac{\text{d}^2q}{\text{d}t^2}+R\frac{\text{d}q}{\text{d}t}+\left ( \frac{1}{c} \right )q$ (公式3)
通过比较公式1和公式3,我们将得到平移机械系统和电气系统的类比量。下表显示了这些类比量。
| 平移机械系统 | 电气系统 |
|---|---|
| 力(F) | 电压(V) |
| 质量(M) | 电感(L) |
| 摩擦系数(B) | 电阻(R) |
| 弹簧常数(K) | 电容的倒数 $(\frac{1}{c})$ |
| 位移(x) | 电荷(q) |
| 速度(v) | 电流(i) |
类似地,旋转机械系统存在转矩-电压类比。现在让我们讨论一下这种类比。
转矩-电压类比
在这种类比中,将旋转机械系统的数学方程与电气系统的网孔方程进行比较。
旋转机械系统如下图所示。
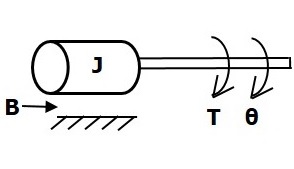
转矩平衡方程为
$$T=T_j+T_b+T_k$$
$\Rightarrow T=J\frac{\text{d}^2\theta}{\text{d}t^2}+B\frac{\text{d}\theta}{\text{d}t}+k\theta$ (公式4)
通过比较公式4和公式3,我们将得到旋转机械系统和电气系统的类比量。下表显示了这些类比量。
| 旋转机械系统 | 电气系统 |
|---|---|
| 转矩(T) | 电压(V) |
| 转动惯量(J) | 电感(L) |
| 旋转摩擦系数(B) | 电阻(R) |
| 扭转弹簧常数(K) | 电容的倒数 $(\frac{1}{c})$ |
| 角位移(θ) | 电荷(q) |
| 角速度(ω) | 电流(i) |
力-电流类比
在力-电流类比中,将平移机械系统的数学方程与电气系统的节点方程进行比较。
考虑以下所示的电气系统。该电路由电流源、电阻器、电感器和电容器组成。所有这些元件都并联连接。
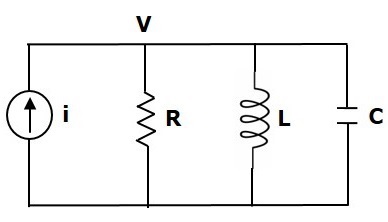
节点方程为
$i=\frac{V}{R}+\frac{1}{L}\int Vdt+C\frac{\text{d}V}{\text{d}t}$ (公式5)
将$V=\frac{\text{d}\Psi}{\text{d}t}$代入公式5。
$$i=\frac{1}{R}\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi+C\frac{\text{d}^2\Psi}{\text{d}t^2}$$
$\Rightarrow i=C\frac{\text{d}^2\Psi}{\text{d}t^2}+\left ( \frac{1}{R} \right )\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi$ (公式6)
通过比较公式1和公式6,我们将得到平移机械系统和电气系统的类比量。下表显示了这些类比量。
| 平移机械系统 | 电气系统 |
|---|---|
| 力(F) | 电流(i) |
| 质量(M) | 电容(C) |
| 摩擦系数(B) | 电阻的倒数$(\frac{1}{R})$ |
| 弹簧常数(K) | 电感的倒数$(\frac{1}{L})$ |
| 位移(x) | 磁通量(ψ) |
| 速度(v) | 电压(V) |
类似地,旋转机械系统存在转矩-电流类比。现在让我们讨论一下这种类比。
转矩-电流类比
在这种类比中,将旋转机械系统的数学方程与电气系统的节点网孔方程进行比较。
通过比较公式4和公式6,我们将得到旋转机械系统和电气系统的类比量。下表显示了这些类比量。
| 旋转机械系统 | 电气系统 |
|---|---|
| 转矩(T) | 电流(i) |
| 转动惯量(J) | 电容(C) |
| 旋转摩擦系数(B) | 电阻的倒数$(\frac{1}{R})$ |
| 扭转弹簧常数(K) | 电感的倒数$(\frac{1}{L})$ |
| 角位移(θ) | 磁通量(ψ) |
| 角速度(ω) | 电压(V) |
本章讨论了机械系统的电学类比。这些类比有助于从类似的电气系统研究和分析非电气系统,例如机械系统。
