控制系统 - 反馈

---

---

如果输出或输出的一部分返回到输入端并用作系统输入的一部分，则称为反馈。反馈在提高控制系统的性能方面发挥着重要作用。在本章中，让我们讨论反馈的类型和反馈的影响。

反馈类型

反馈主要分为两种类型：

• 正反馈
• 负反馈

正反馈

正反馈将参考输入 $R(s)$ 和反馈输出相加。下图显示了正反馈控制系统的方框图。

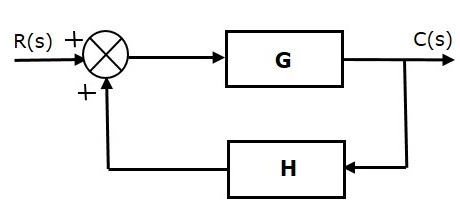
传递函数的概念将在后面的章节中讨论。目前，考虑正反馈控制系统的传递函数为：

$T=\frac{G}{1-GH}$ (公式 1)

其中，

• T 是正反馈控制系统的传递函数或总增益。

• G 是开环增益，它是频率的函数。

• H 是反馈路径的增益，它是频率的函数。

负反馈

负反馈减少了参考输入 $R(s)$ 和系统输出之间的误差。下图显示了负反馈控制系统的方框图。

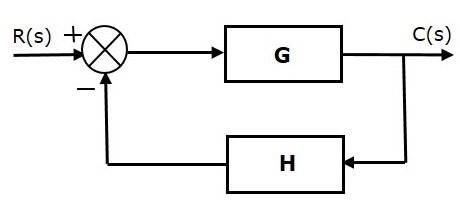
负反馈控制系统的传递函数为：

$T=\frac{G}{1+GH}$ (公式 2)

其中，

• T 是负反馈控制系统的传递函数或总增益。

• G 是开环增益，它是频率的函数。

• H 是反馈路径的增益，它是频率的函数。

上述传递函数的推导在后面的章节中给出。

反馈的影响

现在让我们了解反馈的影响。

反馈对总增益的影响

• 从公式 2 可以看出，负反馈闭环控制系统的总增益是 'G' 与 (1+GH) 的比值。因此，总增益可能会增加或减少，具体取决于 (1+GH) 的值。

• 如果 (1+GH) 的值小于 1，则总增益增加。在这种情况下，'GH' 值为负，因为反馈路径的增益为负。

• 如果 (1+GH) 的值大于 1，则总增益减小。在这种情况下，'GH' 值为正，因为反馈路径的增益为正。

通常，'G' 和 'H' 都是频率的函数。因此，反馈将在一个频率范围内提高系统的总增益，而在另一个频率范围内降低。

反馈对灵敏度的影响

负反馈闭环控制系统（T）的总增益对开环增益（G）变化的灵敏度定义为

$S_{G}^{T} = \frac{\frac{\partial T}{T}}{\frac{\partial G}{G}}=\frac{T 的百分比变化}{G 的百分比变化}$ (公式 3)

其中，∂T 是由于 G 的增量变化而引起的 T 的增量变化。

我们可以将公式 3 重写为

$S_{G}^{T}=\frac{\partial T}{\partial G}\frac{G}{T}$ (公式 4)

对公式 2 的两边关于 G 进行偏微分。

$\frac{\partial T}{\partial G}=\frac{\partial}{\partial G}\left (\frac{G}{1+GH} \right )=\frac{(1+GH).1-G(H)}{(1+GH)^2}=\frac{1}{(1+GH)^2}$ (公式 5)

从公式 2，我们可以得到

$\frac{G}{T}=1+GH$ (公式 6)

将公式 5 和公式 6 代入公式 4。

$$S_{G}^{T}=\frac{1}{(1+GH)^2}(1+GH)=\frac{1}{1+GH}$$

因此，我们得到了闭环控制系统总增益的灵敏度为 (1+GH) 的倒数。因此，灵敏度可能会增加或减少，具体取决于 (1+GH) 的值。

• 如果 (1+GH) 的值小于 1，则灵敏度增加。在这种情况下，'GH' 值为负，因为反馈路径的增益为负。

• 如果 (1+GH) 的值大于 1，则灵敏度降低。在这种情况下，'GH' 值为正，因为反馈路径的增益为正。

通常，'G' 和 'H' 都是频率的函数。因此，反馈将在一个频率范围内提高系统增益的灵敏度，而在另一个频率范围内降低。因此，我们必须选择 'GH' 的值，使系统对参数变化不敏感或不太敏感。

反馈对稳定性的影响

• 如果系统的输出处于控制之下，则称该系统是稳定的。否则，则称其为不稳定的。

• 在公式 2 中，如果分母值为零（即 GH = -1），则控制系统的输出将为无穷大。因此，控制系统变得不稳定。

因此，我们必须正确选择反馈以使控制系统稳定。

反馈对噪声的影响

为了了解反馈对噪声的影响，让我们比较有反馈和无反馈时由于噪声信号单独引起的传递函数关系。

考虑一个开环控制系统，其中包含如下所示的噪声信号。

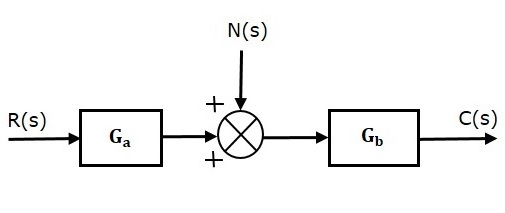
由于噪声信号单独引起的开环传递函数为

$\frac{C(s)}{N(s)}=G_b$ (公式 7)

它是通过将另一个输入 $R(s)$ 设置为零而获得的。

考虑一个闭环控制系统，其中包含如下所示的噪声信号。

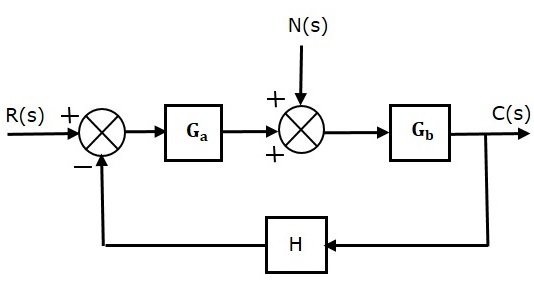
由于噪声信号单独引起的闭环传递函数为

$\frac{C(s)}{N(s)}=\frac{G_b}{1+G_aG_bH}$ (公式 8)

它是通过将另一个输入 $R(s)$ 设置为零而获得的。

比较公式 7 和公式 8，

在闭环控制系统中，由于噪声信号引起的增益降低了 $(1+G_a G_b H)$ 的因子，前提是 $(1+G_a G_b H)$ 大于 1。