机械系统建模

---

---

在本章中，让我们讨论微分方程建模在机械系统中的应用。根据运动类型，机械系统可分为两种。

• 平移机械系统
• 旋转机械系统

平移机械系统的建模

平移机械系统沿直线运动。这些系统主要由三个基本元件组成：质量、弹簧和阻尼器。

如果对平移机械系统施加一个力，那么它会受到系统质量、弹性和摩擦产生的反作用力的阻碍。由于施加的力和反作用力方向相反，因此作用在系统上的所有力的代数和为零。现在让我们分别看看这三个元件产生的反作用力。

质量

质量是物体的一种属性，它存储动能。如果对质量为M的物体施加一个力，那么它会受到质量产生的反作用力的阻碍。这个反作用力与物体的加速度成正比。假设弹性和摩擦可以忽略不计。

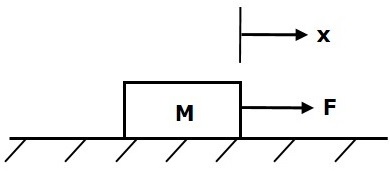
$$F_m\propto\: a$$

$$\Rightarrow F_m=Ma=M\frac{\text{d}^2x}{\text{d}t^2}$$

$$F=F_m=M\frac{\text{d}^2x}{\text{d}t^2}$$

其中，

• F 为施加的力

• F_m 为质量产生的反作用力

• M 为质量

• a 为加速度

• x 为位移

弹簧

弹簧是一种存储势能的元件。如果对弹簧K施加一个力，那么它会受到弹簧弹性产生的反作用力的阻碍。这个反作用力与弹簧的位移成正比。假设质量和摩擦可以忽略不计。

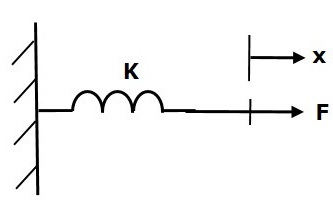
$$F\propto\: x$$

$$\Rightarrow F_k=Kx$$

$$F=F_k=Kx$$

其中，

• F 为施加的力

• F_k 为弹簧弹性产生的反作用力

• K 为弹簧常数

• x 为位移

阻尼器

如果对阻尼器B施加一个力，那么它会受到阻尼器摩擦产生的反作用力的阻碍。这个反作用力与物体的速度成正比。假设质量和弹性可以忽略不计。

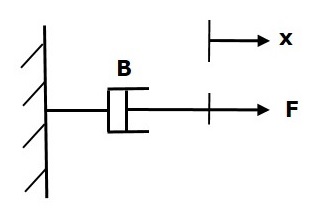
$$F_b\propto\: \nu$$

$$\Rightarrow F_b=B\nu=B\frac{\text{d}x}{\text{d}t}$$

$$F=F_b=B\frac{\text{d}x}{\text{d}t}$$

其中，

• F_b 为阻尼器摩擦产生的反作用力

• B 为摩擦系数

• v 为速度

• x 为位移

旋转机械系统的建模

旋转机械系统绕固定轴旋转。这些系统主要由三个基本元件组成：转动惯量、扭转弹簧和阻尼器。

如果对旋转机械系统施加一个力矩，那么它会受到系统转动惯量、弹性和摩擦产生的反作用力矩的阻碍。由于施加的力矩和反作用力矩方向相反，因此作用在系统上的所有力矩的代数和为零。现在让我们分别看看这三个元件产生的反作用力矩。

转动惯量

在平移机械系统中，质量存储动能。类似地，在旋转机械系统中，转动惯量存储动能。

如果对转动惯量为J的物体施加一个力矩，那么它会受到转动惯量产生的反作用力矩的阻碍。这个反作用力矩与物体的角加速度成正比。假设弹性和摩擦可以忽略不计。

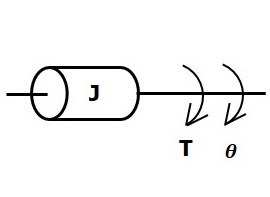
$$T_j\propto\: \alpha$$

$$\Rightarrow T_j=J\alpha=J\frac{\text{d}^2\theta}{\text{d}t^2}$$

$$T=T_j=J\frac{\text{d}^2\theta}{\text{d}t^2}$$

其中，

• T 为施加的力矩

• T_j 为转动惯量产生的反作用力矩

• J 为转动惯量

• α 为角加速度

• θ 为角位移

扭转弹簧

在平移机械系统中，弹簧存储势能。类似地，在旋转机械系统中，扭转弹簧存储势能。

如果对扭转弹簧K施加一个力矩，那么它会受到扭转弹簧弹性产生的反作用力矩的阻碍。这个反作用力矩与扭转弹簧的角位移成正比。假设转动惯量和摩擦可以忽略不计。

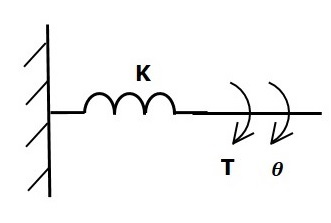
$$T_k\propto\: \theta$$

$$\Rightarrow T_k=K\theta$$

$$T=T_k=K\theta$$

其中，

• T 为施加的力矩

• T_k 为扭转弹簧弹性产生的反作用力矩

• K 为扭转弹簧常数

• θ 为角位移

阻尼器

如果对阻尼器B施加一个力矩，那么它会受到阻尼器旋转摩擦产生的反作用力矩的阻碍。这个反作用力矩与物体的角速度成正比。假设转动惯量和弹性可以忽略不计。

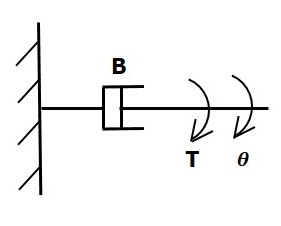
$$T_b\propto\: \omega$$

$$\Rightarrow T_b=B\omega=B\frac{\text{d}\theta}{\text{d}t}$$

$$T=T_b=B\frac{\text{d}\theta}{\text{d}t}$$

其中，

• T_b 为阻尼器旋转摩擦产生的反作用力矩

• B 为旋转摩擦系数

• ω 为角速度

• θ 为角位移