控制系统 - 稳态误差

---

---

控制系统输出在稳态下与期望响应的偏差称为稳态误差。它表示为$e_{ss}$。我们可以使用终值定理来求解稳态误差，如下所示。

$$e_{ss}=\lim_{t \to \infty}e(t)=\lim_{s \to 0}sE(s)$$

其中，

E(s)是误差信号$e(t)$的拉普拉斯变换

让我们分别讨论如何求解单位反馈和非单位反馈控制系统的稳态误差。

单位反馈系统的稳态误差

考虑以下具有单位负反馈的闭环控制系统的框图。

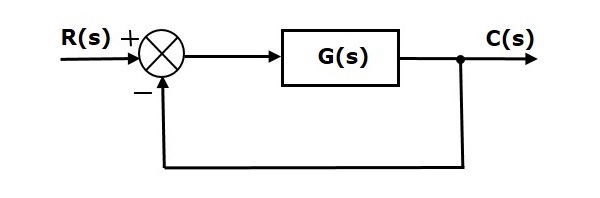
其中，

• R(s)是参考输入信号$r(t)$的拉普拉斯变换
• C(s)是输出信号$c(t)$的拉普拉斯变换

我们知道单位负反馈闭环控制系统的传递函数为

$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$

$$\Rightarrow C(s)=\frac{R(s)G(s)}{1+G(s)}$$

求和点的输出为：

$$E(s)=R(s)-C(s)$$

将$C(s)$的值代入上式。

$$E(s)=R(s)-\frac{R(s)G(s)}{1+G(s)}$$

$$\Rightarrow E(s)=\frac{R(s)+R(s)G(s)-R(s)G(s)}{1+G(s)}$$

$$\Rightarrow E(s)=\frac{R(s)}{1+G(s)}$$

将$E(s)$的值代入稳态误差公式

$$e_{ss}=\lim_{s \to 0} \frac{sR(s)}{1+G(s)}$$

下表显示了对于单位阶跃、单位斜坡和单位抛物线信号等标准输入信号的稳态误差和误差常数。

其中，$K_p$、$K_v$和$K_a$分别为位置误差常数、速度误差常数和加速度误差常数。

注意 - 如果上述任何输入信号的幅度不为1，则将相应的稳态误差乘以该幅度。

注意 - 我们无法为单位冲激信号定义稳态误差，因为它只存在于原点。因此，我们无法将冲激响应与单位冲激输入进行比较，因为t表示无穷大。

示例

让我们求解输入信号$r(t)=\left( 5+2t+\frac{t^2}{2} \right )u(t)$的稳态误差，该信号具有单位负反馈控制系统，其中$G(s)=\frac{5(s+4)}{s^2(s+1)(s+20)}$

给定的输入信号是三个信号（阶跃、斜坡和抛物线）的组合。下表显示了这三个信号的误差常数和稳态误差值。

我们将通过将上述三个稳态误差相加来获得整体稳态误差。

$$e_{ss}=e_{ss1}+e_{ss2}+e_{ss3}$$

$$\Rightarrow e_{ss}=0+0+1=1$$

因此，在这个例子中，我们得到了稳态误差$e_{ss}$为1。

非单位反馈系统的稳态误差

考虑以下具有非单位负反馈的闭环控制系统的框图。

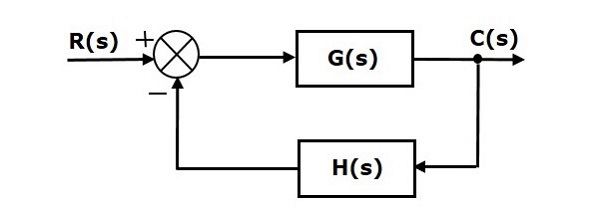
我们只能为单位反馈系统求解稳态误差。因此，我们必须将非单位反馈系统转换为单位反馈系统。为此，在上图中加入一个单位正反馈路径和一个单位负反馈路径。新的框图如下所示。

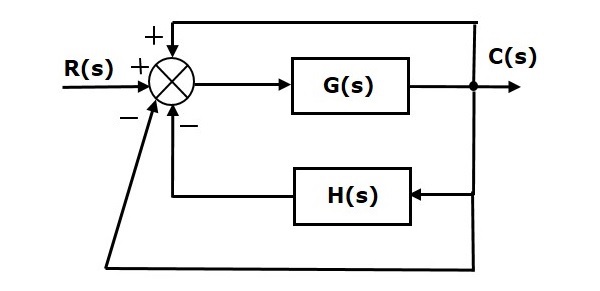
通过保持单位负反馈不变来简化上图。简化后的框图如下所示。

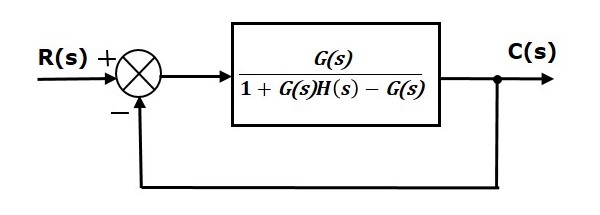
此框图类似于单位负反馈闭环控制系统的框图。这里，单个模块具有传递函数$\frac{G(s)}{1+G(s)H(s)-G(s)}$，而不是$G(s)$。您现在可以使用为单位负反馈系统提供的稳态误差公式来计算稳态误差。

注意 - 对于不稳定的闭环系统，求解稳态误差是没有意义的。因此，我们只需要针对闭环稳定系统计算稳态误差。这意味着在求解稳态误差之前，我们需要检查控制系统是否稳定。在下一章中，我们将讨论与稳定性相关的概念。