控制系统 - 控制器

---

---

各种类型的控制器用于提高控制系统的性能。在本章中，我们将讨论基本的控制器，例如比例控制器、微分控制器和积分控制器。

比例控制器

比例控制器产生一个输出，该输出与误差信号成正比。

$$u(t) \propto e(t) $$

$$\Rightarrow u(t)=K_P e(t)$$

对两边应用拉普拉斯变换 -

$$U(s)=K_P E(s)$$

$$\frac{U(s)}{E(s)}=K_P$$

因此，比例控制器的传递函数为 $K_P$。

其中，

U(s) 是执行信号 u(t) 的拉普拉斯变换

E(s) 是误差信号 e(t) 的拉普拉斯变换

K_P 是比例常数

带有比例控制器的单位负反馈闭环控制系统的方框图如下所示。

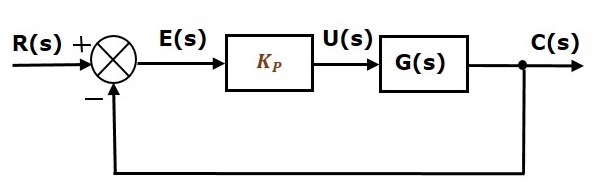
比例控制器用于根据需要更改瞬态响应。

微分控制器

微分控制器产生一个输出，该输出是误差信号的导数。

$$u(t)=K_D \frac{\text{d}e(t)}{\text{d}t}$$

对两边应用拉普拉斯变换。

$$U(s)=K_D sE(s)$$

$$\frac{U(s)}{E(s)}=K_D s$$

因此，微分控制器的传递函数为 $K_D s$。

其中，$K_D$ 是微分常数。

带有微分控制器的单位负反馈闭环控制系统的方框图如下所示。

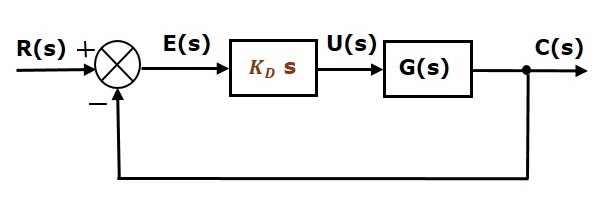
微分控制器用于将不稳定的控制系统转变为稳定的控制系统。

积分控制器

积分控制器产生一个输出，该输出是误差信号的积分。

$$u(t)=K_I \int e(t) dt$$

对两边应用拉普拉斯变换 -

$$U(s)=\frac{K_I E(s)}{s}$$

$$\frac{U(s)}{E(s)}=\frac{K_I}{s}$$

因此，积分控制器的传递函数为 $\frac{K_I}{s}$。

其中，$K_I$ 是积分常数。

带有积分控制器的单位负反馈闭环控制系统的方框图如下所示。

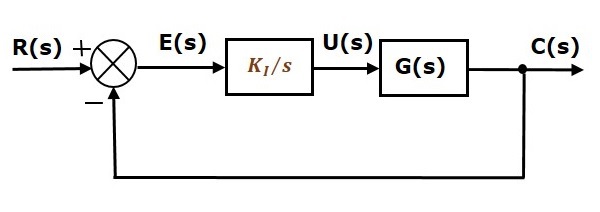
积分控制器用于减小稳态误差。

现在让我们讨论一下基本控制器的组合。

比例微分 (PD) 控制器

比例微分控制器产生一个输出，该输出是比例控制器和微分控制器的输出的组合。

$$u(t)=K_P e(t)+K_D \frac{\text{d}e(t)}{\text{d}t}$$

对两边应用拉普拉斯变换 -

$$U(s)=(K_P+K_D s)E(s)$$

$$\frac{U(s)}{E(s)}=K_P+K_D s$$

因此，比例微分控制器的传递函数为 $K_P + K_D s$。

带有比例微分控制器的单位负反馈闭环控制系统的方框图如下所示。

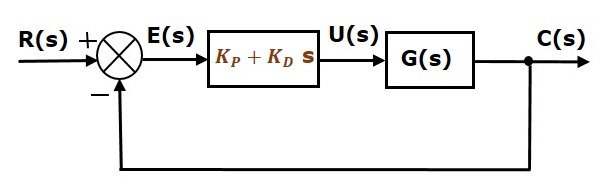
比例微分控制器用于提高控制系统的稳定性，而不影响稳态误差。

比例积分 (PI) 控制器

比例积分控制器产生一个输出，该输出是比例控制器和积分控制器的输出的组合。

$$u(t)=K_P e(t)+K_I \int e(t) dt$$

对两边应用拉普拉斯变换 -

$$U(s)=\left(K_P+\frac{K_I}{s} \right )E(s)$$

$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}$$

因此，比例积分控制器的传递函数为 $K_P + \frac{K_I} {s}$。

带有比例积分控制器的单位负反馈闭环控制系统的方框图如下所示。

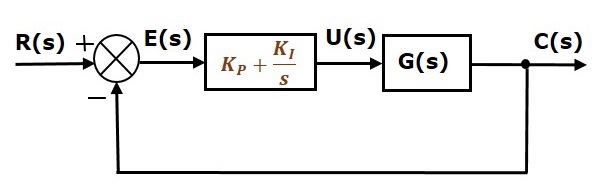
比例积分控制器用于减小稳态误差，而不影响控制系统的稳定性。

比例积分微分 (PID) 控制器

比例积分微分控制器产生一个输出，该输出是比例控制器、积分控制器和微分控制器的输出的组合。

$$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac{\text{d}e(t)}{\text{d}t}$$

对两边应用拉普拉斯变换 -

$$U(s)=\left(K_P+\frac{K_I}{s}+K_D s \right )E(s)$$

$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}+K_D s$$

因此，比例积分微分控制器的传递函数为 $K_P + \frac{K_I} {s} + K_D s$。

带有比例积分微分控制器的单位负反馈闭环控制系统的方框图如下所示。

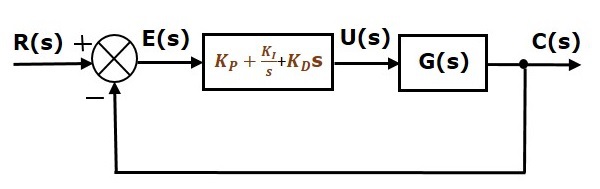
比例积分微分控制器用于提高控制系统的稳定性并减小稳态误差。