控制系统 - 时间响应分析

---

---

我们可以分析控制系统在时域和频域的响应。我们将在后面的章节中讨论控制系统的频率响应分析。现在让我们讨论控制系统的时间响应分析。

什么是时间响应？

如果控制系统对输入的输出随时间变化，则称为控制系统的时间响应。时间响应由两部分组成。

• 暂态响应
• 稳态响应

控制系统在时域的响应如下图所示。

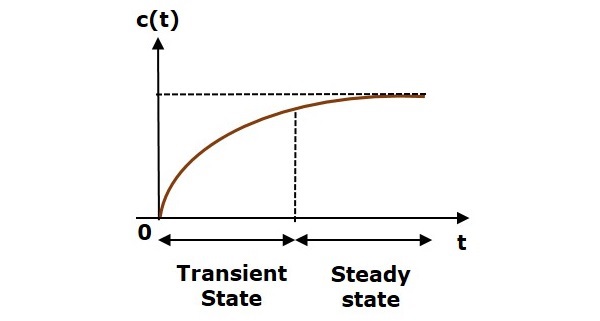
此处，图中同时指出了暂态和稳态。对应于这些状态的响应被称为暂态响应和稳态响应。

数学上，我们可以将时间响应 c(t) 写作

$$c(t)=c_{tr}(t)+c_{ss}(t)$$

其中，

• c_tr(t) 是暂态响应
• c_ss(t) 是稳态响应

暂态响应

对控制系统施加输入后，输出需要一定时间才能达到稳态。因此，在达到稳态之前，输出将处于暂态。因此，控制系统在暂态期间的响应称为**暂态响应**。

对于较大的 ‘t’ 值，暂态响应将为零。理想情况下，这个 ‘t’ 值是无穷大，实际上是五倍常数。

数学上，我们可以写成

$$\lim_{t\rightarrow \infty }c_{tr}(t)=0$$

稳态响应

即使在暂态响应对于较大的 ‘t’ 值为零之后，时间响应中仍然存在的部分称为**稳态响应**。这意味着，即使在稳态期间，暂态响应也将为零。

示例

让我们找到控制系统 $c(t)=10+5e^{-t}$ 的时间响应的暂态和稳态项。

这里，第二项 $5e^{-t}$ 当 **t** 表示无穷大时将为零。所以，这是**暂态项**。而第一项 10 即使当 **t** 趋于无穷大时仍然存在。所以，这是**稳态项**。

标准测试信号

标准测试信号包括脉冲、阶跃、斜坡和抛物线。这些信号用于使用输出的时间响应来了解控制系统的性能。

单位脉冲信号

单位脉冲信号 δ(t) 定义为

$\delta (t)=0$ 对于 $t\neq 0$

以及 $\int_{0^-}^{0^+} \delta (t)dt=1$

下图显示了单位脉冲信号。

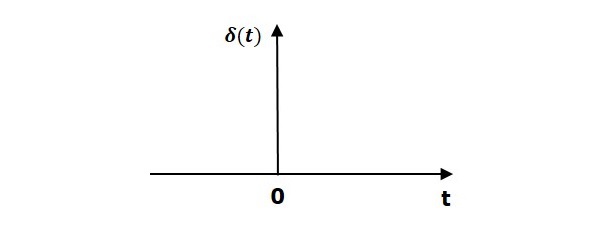
因此，单位脉冲信号仅在 ‘t’ 等于零时存在。该信号在围绕 ‘t’ 的较小时间间隔内的面积等于零为一。对于所有其他 ‘t’ 值，单位脉冲信号的值为零。

单位阶跃信号

单位阶跃信号 u(t) 定义为

$$u(t)=1;t\geq 0$$

$=0; t<0$

下图显示了单位阶跃信号。

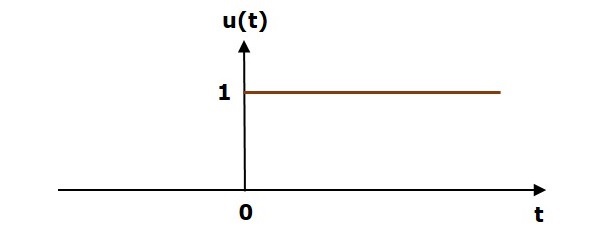
因此，单位阶跃信号存在于所有正 ‘t’ 值（包括零）中。并且在此区间内其值为一。对于所有负 ‘t’ 值，单位阶跃信号的值为零。

单位斜坡信号

单位斜坡信号 r(t) 定义为

$$r(t)=t; t\geq 0$$

$=0; t<0$

我们可以用单位阶跃信号 u(t) 来表示单位斜坡信号 r(t)，如下所示：

$$r(t)=tu(t)$$

下图显示了单位斜坡信号。

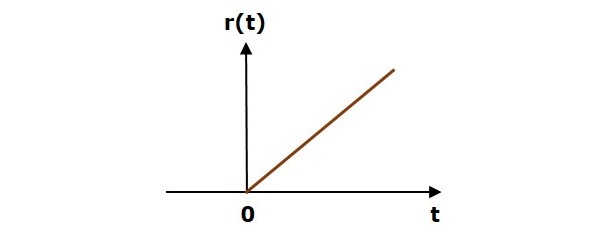
因此，单位斜坡信号存在于所有正 ‘t’ 值（包括零）中。并且在此区间内其值随 ‘t’ 线性增加。对于所有负 ‘t’ 值，单位斜坡信号的值为零。

单位抛物线信号

单位抛物线信号 p(t) 定义为：

$$p(t)=\frac{t^2}{2}; t\geq 0$$

$=0; t<0$

我们可以用单位阶跃信号 u(t) 来表示单位抛物线信号 p(t)，如下所示：

$$p(t)=\frac{t^2}{2}u(t)$$

下图显示了单位抛物线信号。

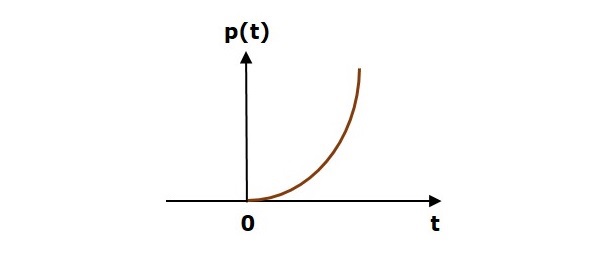
因此，单位抛物线信号存在于所有正 **‘t’** 值（包括零）中。并且在此区间内其值随 ‘t’ 非线性增加。对于所有负 ‘t’ 值，单位抛物线信号的值为零。