时域指标

---

---

在本章中，让我们讨论二阶系统的时域指标。下图显示了二阶系统在欠阻尼情况下的阶跃响应。

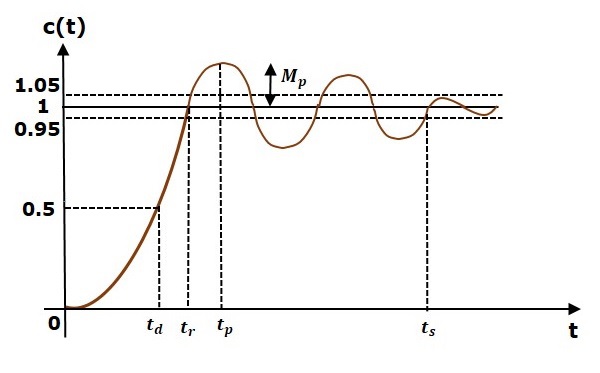
所有时域指标都在此图中表示。响应达到稳定时间之前的部分称为瞬态响应，响应达到稳定时间之后的部分称为稳态响应。

延迟时间

从零时刻开始，响应达到**其最终值的一半**所需的时间。用 $t_d$ 表示。

考虑二阶系统在 t ≥ 0 时的阶跃响应，其中 'δ' 在 0 和 1 之间。

$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$

阶跃响应的最终值为 1。

因此，在 $t=t_d$ 时，阶跃响应的值将为 0.5。将这些值代入上述方程。

$$c(t_d)=0.5=1-\left ( \frac{e^{-\delta\omega_nt_d}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_d+\theta)$$

$$\Rightarrow \left ( \frac{e^{-\delta\omega_nt_d}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_d+\theta)=0.5$$

使用线性近似，可以得到**延迟时间 t_d** 为

$$t_d=\frac{1+0.7\delta}{\omega_n}$$

上升时间

响应从**其最终值的 0% 上升到 100%** 所需的时间。这适用于**欠阻尼系统**。对于过阻尼系统，考虑从最终值的 10% 到 90% 的持续时间。上升时间用**t_r**表示。

在 t = t₁ = 0 时，c(t) = 0。

我们知道阶跃响应的最终值为 1。

因此，在 $t = t_2$ 时，阶跃响应的值为 1。将这些值代入以下方程。

$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$

$$c(t_2)=1=1-\left ( \frac{e^{-\delta\omega_nt_2}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_2+\theta)$$

$$\Rightarrow \left ( \frac{e^{-\delta\omega_nt_2}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_2+\theta)=0$$

$$\Rightarrow \sin(\omega_dt_2+\theta)=0$$

$$\Rightarrow \omega_dt_2+\theta=\pi$$

$$\Rightarrow t_2=\frac{\pi-\theta}{\omega_d}$$

将 t₁ 和 t₂ 的值代入以下**上升时间**方程，

$$t_r=t_2-t_1$$

$$\therefore \: t_r=\frac{\pi-\theta}{\omega_d}$$

从上述方程可以得出，上升时间 $t_r$ 和阻尼频率 $\omega_d$ 成反比。

峰值时间

响应第一次达到**峰值**所需的时间。用 $t_p$ 表示。在 $t = t_p$ 时，响应的一阶导数为零。

我们知道欠阻尼情况下二阶系统的阶跃响应为

$$c(t)=1-\left ( \frac{e^{-\delta \omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$

对 $c(t)$ 求关于 't' 的导数。

$$\frac{\text{d}c(t)}{\text{d}t}=-\left ( \frac{e^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\omega_d\cos(\omega_dt+\theta)-\left ( \frac{-\delta\omega_ne^{-\delta\omega_nt}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt+\theta)$$

将 $t=t_p$ 和 $\frac{\text{d}c(t)}{\text{d}t}=0$ 代入上述方程。

$$0=-\left ( \frac{e^{-\delta\omega_nt_p}}{\sqrt{1-\delta^2}} \right )\left [ \omega_d\cos(\omega_dt_p+\theta)-\delta\omega_n\sin(\omega_dt_p+\theta) \right ]$$

$$\Rightarrow \omega_n\sqrt{1-\delta^2}\cos(\omega_dt_p+\theta)-\delta\omega_n\sin(\omega_dt_p+\theta)=0$$

$$\Rightarrow \sqrt{1-\delta^2}\cos(\omega_dt_p+\theta)-\delta\sin(\omega_dt_p+\theta)=0$$

$$\Rightarrow \sin(\theta)\cos(\omega_dt_p+\theta)-\cos(\theta)\sin(\omega_dt_p+\theta)=0$$

$$\Rightarrow \sin(\theta-\omega_dt_p-\theta)=0$$

$$\Rightarrow sin(-\omega_dt_p)=0\Rightarrow -\sin(\omega_dt_p)=0\Rightarrow sin(\omega_dt_p)=0$$

$$\Rightarrow \omega_dt_p=\pi$$

$$\Rightarrow t_p=\frac{\pi}{\omega_d}$$

从上述方程可以得出，峰值时间 $t_p$ 和阻尼频率 $\omega_d$ 成反比。

峰值超调量

峰值超调量 **M_p** 定义为响应在峰值时间处的偏差与响应的最终值之差。也称为**最大超调量**。

数学上，可以写成

$$M_p=c(t_p)-c(\infty)$$

其中，

c(t_p) 是响应的峰值。

c(∞) 是响应的最终（稳态）值。

在 $t = t_p$ 时，响应 c(t) 为 -

$$c(t_p)=1-\left ( \frac{e^{-\delta\omega_nt_p}}{\sqrt{1-\delta^2}} \right )\sin(\omega_dt_p+\theta)$$

将 $t_p=\frac{\pi}{\omega_d}$ 代入上述方程的右侧。

$$c(t_P)=1-\left ( \frac{e^{-\delta\omega_n\left ( \frac{\pi}{\omega_d} \right )}}{\sqrt{1-\delta^2}} \right )\sin\left ( \omega_d\left ( \frac{\pi}{\omega_d} \right ) +\theta\right )$$

$$\Rightarrow c(t_p)=1-\left ( \frac{e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}}{\sqrt{1-\delta^2}} \right )(-\sin(\theta))$$

我们知道

$$\sin(\theta)=\sqrt{1-\delta^2}$$

所以，我们将得到 c(t_p) 为

$$c(t_p)=1+e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}$$

将 $c(t_p)$ 和 $c(\infty)$ 的值代入峰值超调量方程。

$$M_p=1+e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}-1$$

$$\Rightarrow M_p=e^{-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )}$$

**峰值超调量的百分比 %** $M_p$ 可以用此公式计算。

$$\%M_p=\frac{M_p}{c(\infty )}\times 100\%$$

将 $M_p$ 和 $c(\infty)$ 的值代入上述公式，我们将得到峰值超调量的百分比 $\%M_p$ 为

$$\%M_p=\left ( e^ {-\left ( \frac{\delta\pi}{\sqrt{1-\delta^2}} \right )} \right )\times 100\%$$

从上述方程可以得出，如果阻尼比 $\delta$ 增大，则峰值超调量的百分比 $\% M_p$ 将减小。

稳定时间

响应达到稳态并在最终值周围的指定容差范围内保持的时间。通常，容差范围为 2% 和 5%。稳定时间用 $t_s$ 表示。

5% 容差范围的稳定时间为 -

$$t_s=\frac{3}{\delta\omega_n}=3\tau$$

2% 容差范围的稳定时间为 -

$$t_s=\frac{4}{\delta\omega_n}=4\tau$$

其中，$\tau$ 为时间常数，等于 $\frac{1}{\delta\omega_n}$。

• 稳定时间 $t_s$ 和时间常数 $\tau$ 均与阻尼比 $\delta$ 成反比。

• 稳定时间 $t_s$ 和时间常数 $\tau$ 均与系统增益无关。这意味着即使系统增益发生变化，稳定时间 $t_s$ 和时间常数 $\tau$ 也不会改变。

示例

现在让我们找到一个控制系统的时域指标，该系统具有闭环传递函数 $\frac{4}{s^2+2s+4}$，当单位阶跃信号作为输入应用于该控制系统时。

我们知道二阶闭环控制系统的传递函数的标准形式为

$$\frac{\omega_n^2}{s^2+2\delta\omega_ns+\omega_n^2}$$

通过将这两个传递函数相等，我们将得到无阻尼自然频率 $\omega_n$ 为 2 rad/sec，阻尼比 $\delta$ 为 0.5。

我们知道阻尼频率 $\omega_d$ 的公式为

$$\omega_d=\omega_n\sqrt{1-\delta^2}$$

将 $\omega_n$ 和 $\delta$ 的值代入上述公式。

$$\Rightarrow \omega_d=2\sqrt{1-(0.5)^2}$$

$$\Rightarrow \omega_d=1.732 \: rad/sec$$

将 $\delta$ 的值代入以下关系

$$\theta=\cos^{-1}\delta$$

$$\Rightarrow \theta=\cos^{-1}(0.5)=\frac{\pi}{3}\:rad$$

将上述必要的值代入每个时域指标的公式并进行简化，以便获得给定传递函数的时域指标的值。

下表显示了时域指标的公式、必要值的代入和最终值。