控制系统 - 方块图

---

---

方块图由单个方块或多个方块组合而成。它们用于以图形方式表示控制系统。

方块图的基本要素

方块图的基本要素包括方块、加法点和取样点。让我们考虑以下图所示的闭环控制系统的方块图来识别这些元素。

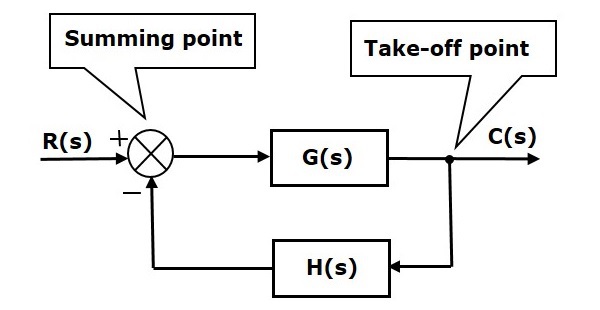
上述方块图包含两个具有传递函数 G(s) 和 H(s) 的方块。它还包含一个加法点和一个取样点。箭头指示信号流的方向。现在让我们逐一讨论这些元素。

方块

组件的传递函数由方块表示。方块具有单个输入和单个输出。

下图显示了一个具有输入 X(s)、输出 Y(s) 和传递函数 G(s) 的方块。

传递函数，$G(s)=\frac{Y(s)}{X(s)}$

$$\Rightarrow Y(s)=G(s)X(s)$$

方块的输出是通过将方块的传递函数乘以输入得到的。

加法点

加法点用一个内部带有十字 (X) 的圆圈表示。它有两个或多个输入和一个输出。它产生输入的代数和。它还可以根据输入的极性执行输入的求和或减法或求和和减法的组合。让我们逐一了解这三种运算。

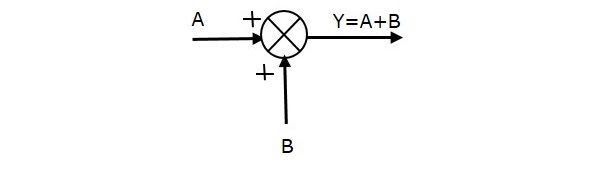
下图显示了具有两个输入 (A、B) 和一个输出 (Y) 的加法点。这里，输入 A 和 B 具有正号。因此，加法点产生输出 Y 为A 和 B 的和。

即，Y = A + B。

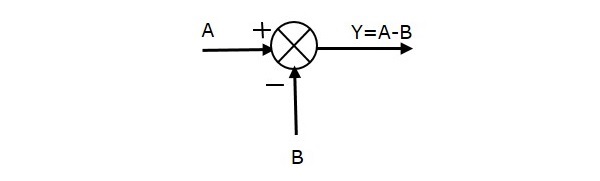
下图显示了具有两个输入 (A、B) 和一个输出 (Y) 的加法点。这里，输入 A 和 B 具有相反的符号，即 A 具有正号，B 具有负号。因此，加法点产生输出Y为A 和 B 的差。

Y = A + (-B) = A - B。

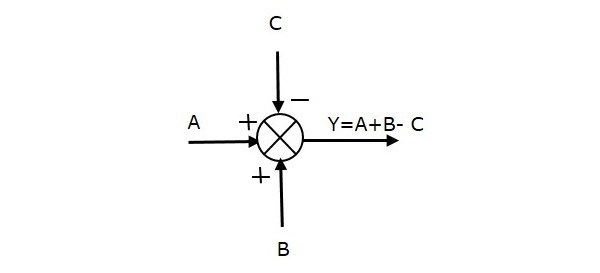
下图显示了具有三个输入 (A、B、C) 和一个输出 (Y) 的加法点。这里，输入 A 和 B 具有正号，C 具有负号。因此，加法点产生输出Y为

Y = A + B + (−C) = A + B − C。

取样点

取样点是一个点，从中可以将相同的输入信号传递到多个分支。这意味着借助取样点，我们可以将相同的输入应用于一个或多个方块、加法点。

在下图中，取样点用于将相同的输入 R(s) 连接到两个或多个方块。

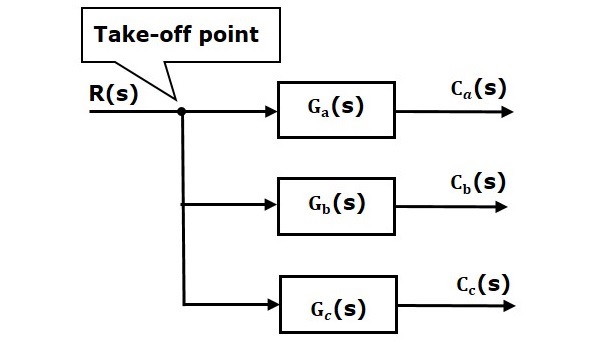
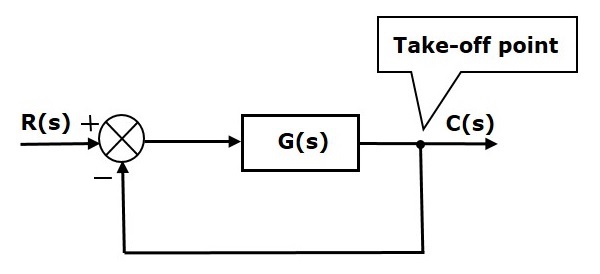
在下图中，取样点用于将输出 C(s) 作为其中一个输入连接到加法点。

电气系统的方块图表示

在本节中，让我们用方块图表示一个电气系统。电气系统主要包含三个基本元件——电阻器、电感器和电容器。

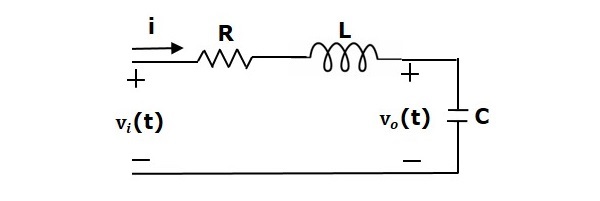
考虑以下图所示的 RLC 串联电路。其中，V_i(t) 和 V_o(t) 分别为输入电压和输出电压。设 i(t) 为流过电路的电流。该电路处于时域。

通过对该电路应用拉普拉斯变换，将得到 s 域中的电路。电路如下图所示。

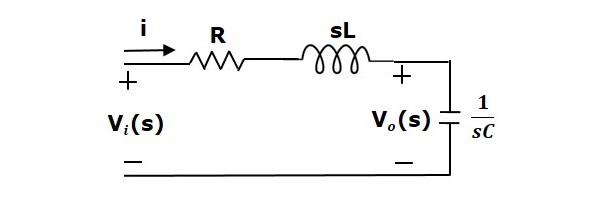
从上述电路，我们可以写出

$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$

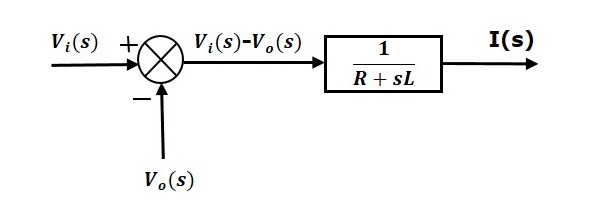
$\Rightarrow I(s)=\left \{ \frac{1}{R+sL} \right \}\left \{ V_i(s)-V_o(s) \right \}$ (公式 1)

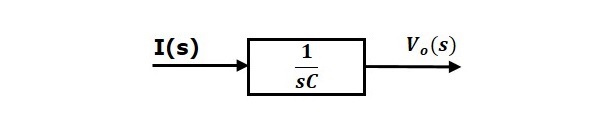
$V_o(s)=\left ( \frac{1}{sC} \right )I(s)$ (公式 2)

现在让我们分别绘制这两个公式的方块图。然后将这些方块图正确地组合起来，以获得 RLC 串联电路（s 域）的整体方块图。

公式 1 可以用一个具有传递函数 $\frac{1}{R+sL}$ 的方块来实现。该方块的输入和输出分别是 $\left \{ V_i(s)-V_o(s) \right \}$ 和 $I(s)$。我们需要一个加法点来获得 $\left \{ V_i(s)-V_o(s) \right \}$。公式 1 的方块图如下图所示。

公式 2 可以用一个具有传递函数 $\frac{1}{sC}$ 的方块来实现。该方块的输入和输出分别是 $I(s)$ 和 $V_o(s)$。公式 2 的方块图如下图所示。

RLC 串联电路（s 域）的整体方块图如下图所示。

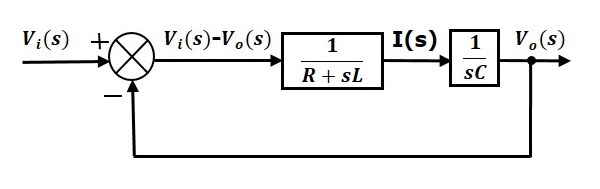
同样，您只需遵循此简单过程即可绘制任何电气电路或系统的方块图。

• 通过应用拉普拉斯变换，将时域电气电路转换为 s 域电气电路。

• 写下流过所有串联支路元件的电流和跨越所有并联支路的电压的方程。

• 分别绘制所有上述方程的方块图。

• 将所有这些方块图正确地组合起来，以获得电气电路（s 域）的整体方块图。