
- 控制系统教程
- 控制系统 - 首页
- 控制系统 - 简介
- 控制系统 - 反馈
- 数学模型
- 机械系统的建模
- 机械系统的电气模拟
- 控制系统 - 方框图
- 方框图代数
- 方框图简化
- 信号流图
- 梅森增益公式
- 时间响应分析
- 一阶系统的响应
- 二阶系统的响应
- 时域指标
- 稳态误差
- 控制系统 - 稳定性
- 控制系统 - 稳定性分析
- 控制系统 - 根轨迹
- 根轨迹的绘制
- 频率响应分析
- 控制系统 - 波德图
- 波德图的绘制
- 控制系统 - 极坐标图
- 控制系统 - 奈奎斯特图
- 控制系统 - 补偿器
- 控制系统 - 控制器
- 控制系统 - 状态空间模型
- 状态空间分析
- 控制系统有用资源
- 控制系统 - 快速指南
- 控制系统 - 有用资源
- 控制系统 - 讨论
控制系统 - 极坐标图
在之前的章节中,我们讨论了波德图。在那里,我们分别绘制了幅值和相位与频率的关系曲线。现在让我们讨论极坐标图。极坐标图是在幅值和相位之间绘制的曲线图。这里,幅值仅用普通值表示。
G(jω)H(jω)的极坐标形式为:
$$G(j\omega)H(j\omega)=|G(j\omega)H(j\omega)| \angle G(j\omega)H(j\omega)$$
极坐标图是通过改变ω从零到∞来绘制G(jω)H(jω)的幅值和相位角之间的曲线图。极坐标图纸如下所示。
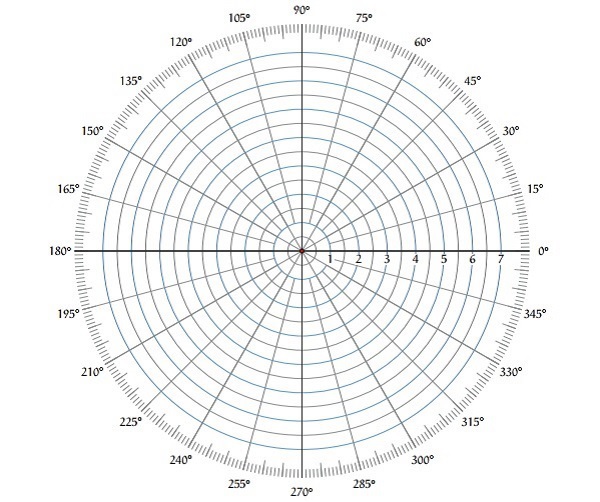
该图纸由同心圆和径向线组成。同心圆和径向线分别表示幅值和相位角。这些角度以逆时针方向用正值表示。类似地,我们可以用顺时针方向的负值表示角度。例如,逆时针方向的2700角等于顺时针方向的−900角。
绘制极坐标图的规则
请遵循以下规则绘制极坐标图。
在开环传递函数中,将s替换为jω。
写出G(jω)H(jω)的幅值和相位的表达式。
通过将ω=0代入,找到G(jω)H(jω)的起始幅值和相位。因此,极坐标图从此幅值和相位角开始。
通过将ω=∞代入,找到G(jω)H(jω)的结束幅值和相位。因此,极坐标图以此幅值和相位角结束。
检查极坐标图是否与实轴相交,方法是将G(jω)H(jω)的虚数项设为零,并找到ω的值。
检查极坐标图是否与虚轴相交,方法是将G(jω)H(jω)的实数项设为零,并找到ω的值。
为了更清晰地绘制极坐标图,请考虑ω的其他值,找到G(jω)H(jω)的幅值和相位。
示例
考虑闭环控制系统的开环传递函数。
$$G(s)H(s)=\frac{5}{s(s+1)(s+2)}$$
让我们使用上述规则绘制该控制系统的极坐标图。
步骤1 - 在开环传递函数中,将s替换为jω。
$$G(j\omega)H(j\omega)=\frac{5}{j\omega(j\omega+1)(j\omega+2)}$$
开环传递函数的幅值为:
$$M=\frac{5}{\omega(\sqrt{\omega^2+1})(\sqrt{\omega^2+4})}$$
开环传递函数的相位角为:
$$\phi=-90^0-\tan^{-1}\omega-\tan^{-1}\frac{\omega}{2}$$
步骤2 - 下表显示了开环传递函数在ω=0 rad/sec和ω=∞ rad/sec时的幅值和相位角。
| 频率 (rad/sec) | 幅值 | 相位角 (度) |
|---|---|---|
| 0 | 0 | ∞ |
| 0 | 0 | -90 或 270 |
∞
-270 或 90
因此,极坐标图从(∞,−900)开始,在(0,−2700)结束。括号中的第一项和第二项分别表示幅值和相位角。
步骤3 - 基于起始和结束极坐标,该极坐标图将与负实轴相交。与负实轴对应的相位角为−1800或1800。因此,通过将开环传递函数的相位角等于−1800或1800,我们将得到ω值为√2。
