控制系统 - 信号流图

---

---

信号流图是代数方程的图形表示。本章将讨论与信号流图相关的基本概念，并学习如何绘制信号流图。

信号流图的基本元素

节点和分支是信号流图的基本元素。

节点

节点是一个点，表示变量或信号。节点有三种类型：输入节点、输出节点和混合节点。

• 输入节点- 只有输出分支的节点。

• 输出节点- 只有输入分支的节点。

• 混合节点- 既有输入分支也有输出分支的节点。

示例

让我们考虑以下信号流图来识别这些节点。

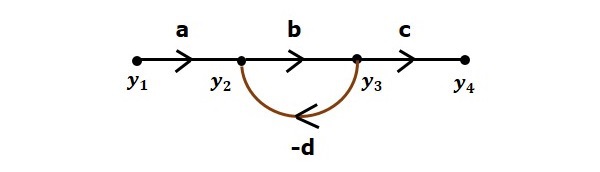
• 此信号流图中的节点为y₁, y₂, y₃和y₄。

• y₁和y₄分别是输入节点和输出节点。

• y₂和y₃是混合节点。

分支

分支是连接两个节点的线段。它既有增益也有方向。例如，上述信号流图中有四个分支。这些分支的增益为a, b, c和-d。

信号流图的绘制

让我们考虑以下代数方程来绘制信号流图：

$$y_2=a_{12}y_1+a_{42}y_4$$

$$y_3=a_{23}y_2+a_{53}y_5$$

$$y_4=a_{34}y_3$$

$$y_5=a_{45}y_4+a_{35}y_3$$

$$y_6=a_{56}y_5$$

该信号流图将有六个节点(y₁, y₂, y₃, y₄, y₅和y₆)和八个分支。分支的增益为a₁₂, a₂₃, a₃₄, a₄₅, a₅₆, a₄₂, a₅₃和a₃₅。

要获得整体信号流图，请为每个方程绘制信号流图，然后组合所有这些信号流图，然后按照以下步骤操作：

步骤 1 - $y_2 = a_{13}y_1 + a_{42}y_4$ 的信号流图如下所示。

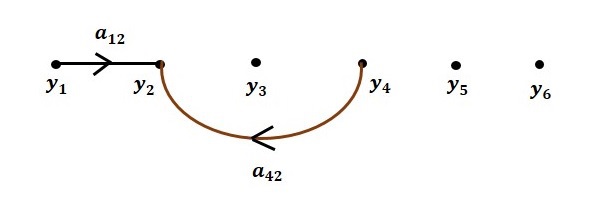
步骤 2 - $y_3 = a_{23}y_2 + a_{53}y_5$ 的信号流图如下所示。

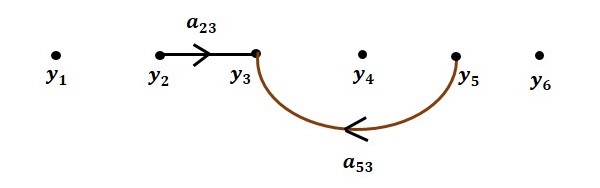
步骤 3 - $y_4 = a_{34}y_3$ 的信号流图如下所示。

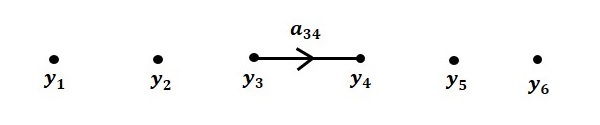
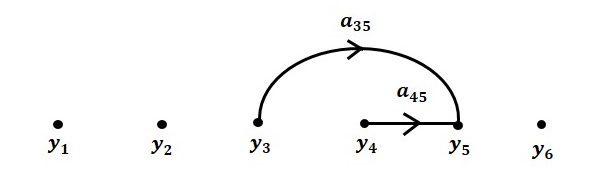
步骤 4 - $y_5 = a_{45}y_4 + a_{35}y_3$ 的信号流图如下所示。

步骤 5 - $y_6 = a_{56}y_5$ 的信号流图如下所示。

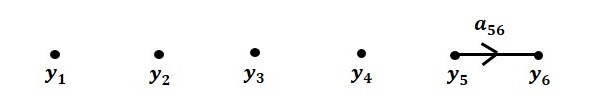
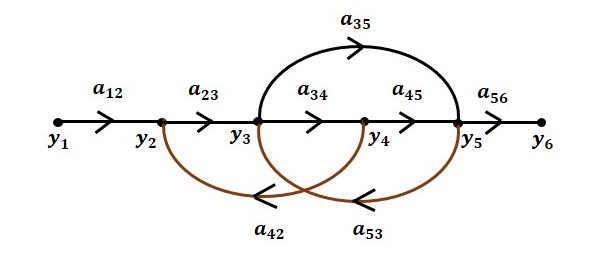
步骤 6 - 整体系统的信号流图如下所示。

将方块图转换为信号流图

按照以下步骤将方块图转换为其等效信号流图。

• 将方块图的所有信号、变量、加法点和取样点表示为信号流图中的节点。

• 将方块图中的方块表示为信号流图中的分支。

• 将方块图中方块内的传递函数表示为信号流图中分支的增益。

• 根据方块图连接节点。如果两个节点之间有连接（但中间没有方块），则将分支的增益表示为1。例如，加法点之间，加法点和取样点之间，输入和加法点之间，取样点和输出之间。

示例

让我们将下面的方块图转换为其等效信号流图。

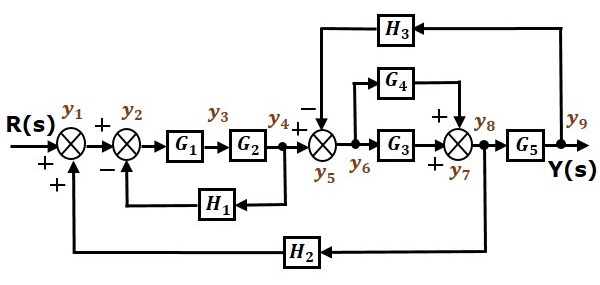
将方块图的输入信号$R(s)$和输出信号$C(s)$表示为信号流图的输入节点$R(s)$和输出节点$C(s)$。

仅供参考，方块图中标注了其余节点（y₁到y₉）。除了输入和输出节点外，还有九个节点。即四个加法点的四个节点，四个取样点的四个节点，以及$G_1$和$G_2$方块之间的变量的一个节点。

下图显示了等效信号流图。

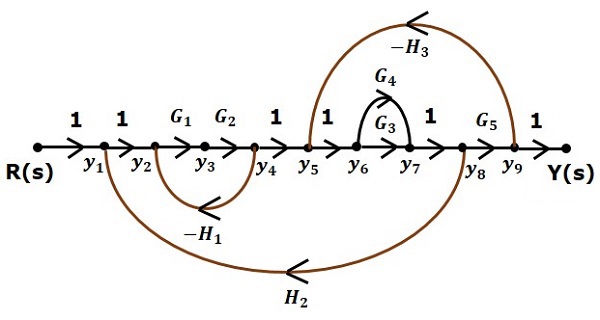
借助梅森增益公式（下一章讨论），您可以计算此信号流图的传递函数。这是信号流图的优势。在这里，我们不需要简化（简化）信号流图来计算传递函数。