MATLAB - 二维数组插值

上一页
下一页

在 MATLAB 中，二维数组插值是一种用于估计二维网格点之间值的方法。这对于创建数据的更平滑表示或提高图像分辨率很有用。interp2 函数通常用于二维数组插值。

语法

Vq = interp2(X,Y,V,Xq,Yq)
Vq = interp2(V,Xq,Yq)
Vq = interp2(V)
Vq = interp2(V,k)
Vq = interp2(___,method)

解释

Vq = interp2(X,Y,V,Xq,Yq) 是 MATLAB 中的一个函数，可帮助您估计网格点之间的值。当您在网格 (X, Y) 中有一组点及其对应的函数值 (V) 时，interp2 可以使用线性插值计算网格中其他点 (Xq, Yq) 处的函数值。插值值始终位于原始网格上。

Vq = interp2(V,Xq,Yq) 即使不指定精确点，也可以估计网格中的值。它假设一个覆盖整个输入网格 V 的默认网格。当您想要节省内存并且不需要知道点之间精确距离时，此默认网格很有用。

Vq = interp2(V) 即使不指定精确点，也可以估计网格中的值。它假设一个覆盖整个输入网格 V 的默认网格。当您想要节省内存并且不需要知道点之间精确距离时，此默认网格很有用。

Vq = interp2(V,k) 可以通过划分样本值之间的间隔来估计网格中的值。参数 k 指定划分间隔的次数。这会创建一个更精细的网格，在原始样本值之间具有更多插值点。

Vq = interp2(___,method) 允许您选择如何在网格上的点之间估计值。您可以使用诸如 'linear'、'nearest'、'cubic'、'makima' 或 'spline' 之类的方法。默认方法为 'linear'，它在点之间创建直线。

数组插值的示例

这里让我们尝试一些使用上面提到的语法的数组插值示例。

示例 1

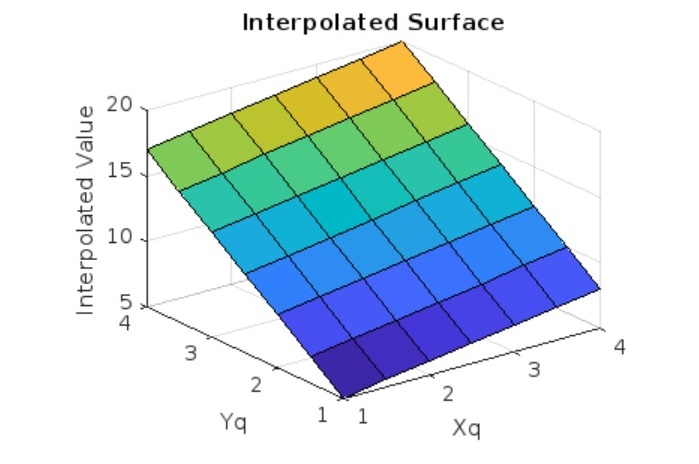
以下是如何使用Vq = interp2(X,Y,V,Xq,Yq)计算数组插值的示例 -

[X, Y] = meshgrid(1:4, 1:4);
V = [5 6 7 8; 9 10 11 12; 13 14 15 16; 17 18 19 20];

[Xq, Yq] = meshgrid(1:0.5:4, 1:0.5:4);

% Perform 2D linear interpolation
Vq = interp2(X, Y, V, Xq, Yq);

% Plot the original surface
figure;
surf(X, Y, V);
title('Original Surface');
xlabel('X');
ylabel('Y');
zlabel('Value');

% Plot the interpolated surface
figure;
surf(Xq, Yq, Vq);
title('Interpolated Surface');
xlabel('Xq');
ylabel('Yq');
zlabel('Interpolated Value');

在上面的示例中，我们有 -

  • 我们首先使用 meshgrid 创建一个样本点 (X, Y) 网格。此网格中的每个点对应于矩阵 V 中的一个值。
  • 接下来，我们通过在每个维度上将样本点之间的间隔除以 2 来创建一个更精细的查询点 (Xq, Yq) 网格。这些是我们想要插值值的点。
  • 我们使用 interp2 函数对原始网格 (X, Y) 使用查询点 (Xq, Yq) 执行线性插值。
  • 我们使用 surf 函数创建原始数据 (X, Y, V) 的曲面图。这显示了由矩阵 V 表示的原始曲面。
  • 我们再次使用 surf 函数创建插值值 (Xq, Yq, Vq) 的曲面图。这显示了插值如何估计查询点 (Xq, Yq) 处的值。
  • 通过比较原始曲面和插值曲面，我们可以直观地看到插值如何填充原始数据点之间的间隙。

在代码执行时，我们得到的输出如下 -

interpolated surface

示例 2

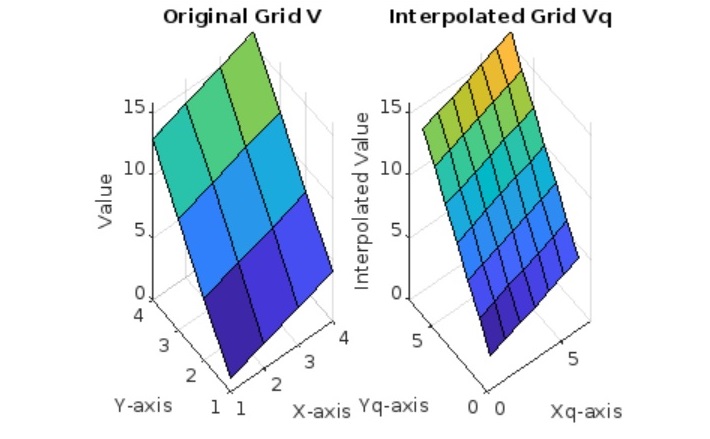
以下是如何使用Vq = interp2(V,Xq,Yq)计算数组插值的示例 -

V = [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16];

[Xq, Yq] = meshgrid(1:0.5:4, 1:0.5:4);

Vq = interp2(V, Xq, Yq);

% Plot the original grid V
subplot(1, 2, 1);
surf(V);
title('Original Grid V');
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Value');

% Plot the interpolated grid Vq
subplot(1, 2, 2);
surf(Vq);
title('Interpolated Grid Vq');
xlabel('Xq-axis');
ylabel('Yq-axis');
zlabel('Interpolated Value');

在上面的示例中，我们有 -

  • 我们首先定义一个由矩阵 V 表示的 4x4 样本点网格。
  • 我们使用 meshgrid 创建一个更精细的查询点 (Xq, Yq) 网格。这些是我们想要从原始网格插值值的点。
  • 我们使用 interp2 函数对整个输入网格 V 使用查询点 (Xq, Yq) 执行线性插值。
  • 我们使用 surf 函数绘制原始网格 V 和插值网格 Vq 以可视化曲面。子图用于并排显示两个图以进行比较。

执行后的输出如下 -

array interpolation

示例 3

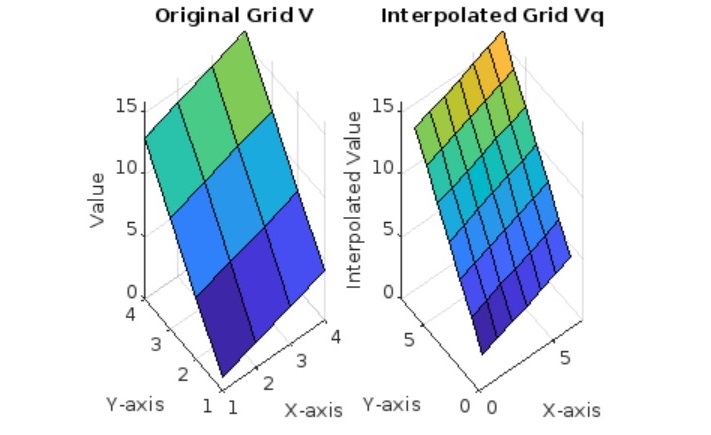
以下是如何使用Vq = interp2(V)计算数组插值的示例 -

V = [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16];

Vq = interp2(V);

% Plot the original grid V
subplot(1, 2, 1);
surf(V);
title('Original Grid V');
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Value');

% Plot the interpolated grid Vq
subplot(1, 2, 2);
surf(Vq);
title('Interpolated Grid Vq');
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Interpolated Value');

在上面的示例中，我们有 -

  • 我们首先定义一个由矩阵 V 表示的 4x4 样本点网格。
  • 我们使用 interp2 函数而不指定 Xq 和 Yq，这会导致它使用一个覆盖整个输入网格 V 的默认网格。此默认网格用于估计中间点的值。
  • 我们使用 surf 函数绘制原始网格 V 和插值网格 Vq 以可视化曲面。子图用于并排显示两个图以进行比较。

在代码执行时，我们得到的输出如下 -

interpolated grid

示例 4

以下是如何使用Vq = interp2(V,k)计算数组插值的示例 -

V = [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16];

k = 2;
Vq = interp2(V, k);

% Plot the original grid V
subplot(1, 2, 1);
surf(V);
title('Original Grid V');
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Value');

% Plot the interpolated grid Vq
subplot(1, 2, 2);
surf(Vq);
title('Interpolated Grid Vq (k=2)');
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Interpolated Value');

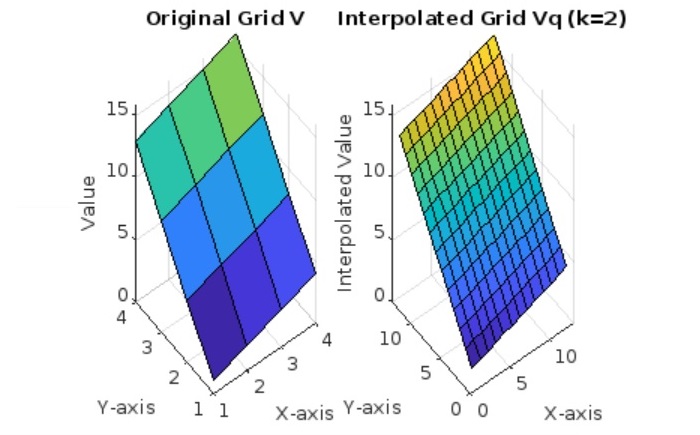
在上面的示例中，我们有 -

  • 我们首先定义一个由矩阵 V 表示的 4x4 样本点网格。
  • 我们使用带参数 k=2 的 interp2 函数，该参数指定样本值之间的间隔应分成两部分。这会创建一个更精细的网格，在原始样本值之间具有更多插值点。
  • 我们使用 surf 函数绘制原始网格 V 和插值网格 Vq 以可视化曲面。子图用于并排显示两个图以进行比较。

在代码执行时，我们得到的输出如下 -

interpolated grid

示例 5

以下是如何使用Vq = interp2(___,method)计算数组插值的示例 -

[X, Y] = meshgrid(-3:0.2:3, -3:0.2:3);

Z = peaks(X, Y);

[Xq, Yq] = meshgrid(-3:0.05:3, -3:0.05:3);

% Perform 2D linear interpolation
Zq = interp2(X, Y, Z, Xq, Yq, 'linear');

% Plot the original and interpolated surfaces
subplot(1, 2, 1);
surf(X, Y, Z);
title('Original Surface');
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Z-axis');

subplot(1, 2, 2);
surf(Xq, Yq, Zq);
title('Interpolated Surface');
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Z-axis');

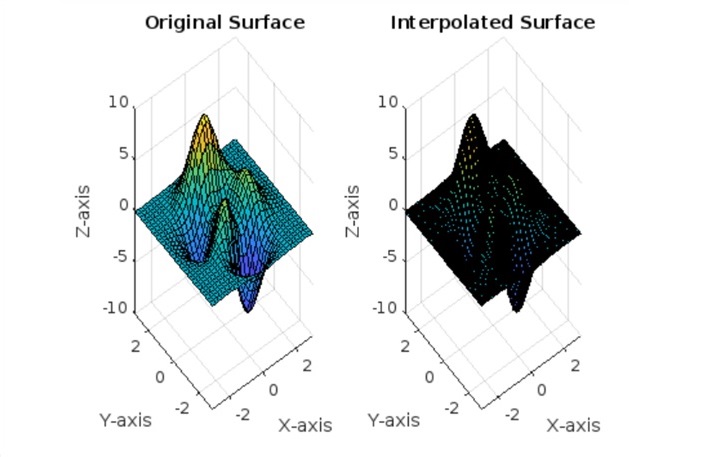
在上面的示例中，我们有 -

  • meshgrid 函数创建了一个从 -3 到 3 跨越的点 (X, Y) 网格，步长为 0.2。
  • 然后使用 peaks 函数根据 X 和 Y 网格计算 Z 值。
  • 另一个网格 (Xq, Yq) 使用更精细的步长 0.05 进行插值。
  • interp2 用于在原始 (X, Y, Z) 网格和更精细的 (Xq, Yq) 网格之间执行二维线性插值，从而产生插值 Zq 值。
  • 原始曲面和插值曲面都使用 surf 函数绘制以可视化插值过程。

在代码执行时，我们得到的输出如下 -

original surface

示例 6

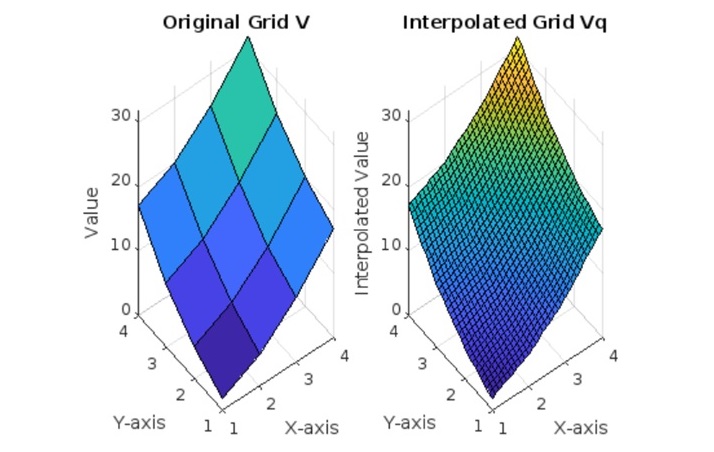
以下是如何在网格上计算数组插值的示例 -

[X, Y] = meshgrid(1:4, 1:4);
V = X.^2 + Y.^2;

[Xq, Yq] = meshgrid(1:0.1:4, 1:0.1:4);

% Perform 2D linear interpolation
Vq = interp2(X, Y, V, Xq, Yq, 'linear');

% Plot the original and interpolated surfaces
subplot(1, 2, 1);
surf(X, Y, V);
title('Original Grid V');
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Value');

subplot(1, 2, 2);
surf(Xq, Yq, Vq);
title('Interpolated Grid Vq');
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Interpolated Value');

在上面的示例中，我们有 -

  • 我们使用 meshgrid 创建一个样本点 (X, Y) 网格。V 定义为 X 和 Y 的函数。在这种情况下，V = X^2 + Y^2。
  • 我们使用 meshgrid 创建一个更精细的网格 (Xq, Yq) 以定义我们想要插值值的点。
  • 我们使用 interp2 函数在点 (Xq, Yq) 处插值 V 的值。'linear' 方法用于插值。
  • 我们使用 surf 函数绘制原始网格 V 和插值网格 Vq 以可视化曲面。子图用于并排显示两个图以进行比较。

在代码执行时，我们得到的输出如下 -

original grid v
打印页面
上一页
下一页
广告