MATLAB - 绘制向量

---

---

在 MATLAB 中，向量是用于存储和处理元素序列的基本数据结构。它们表示可以包含数字、字符、逻辑值或其他 MATLAB 对象的一维数组。

MATLAB 中的向量可以通过几种方式创建：

• 行向量 - 使用方括号创建，元素之间用空格或逗号分隔。例如：v = [1, 2, 3, 4]。
• 列向量 - 与行向量类似，但元素之间用分号分隔以创建列。例如：v = [1; 2; 3; 4]。
• 使用函数 - MATLAB 函数（如 linspace、ones、zeros 和 rand）可以生成具有特定特征的向量（例如，值范围、全是 1、全是 0、随机值）。

MATLAB 中的向量允许进行各种运算，例如加法、减法、逐元素乘法、除法等等。它们在 MATLAB 中的数学计算、信号处理、数据分析和绘图中起着至关重要的作用。

创建 Matlab 向量

创建 Matlab 向量非常容易，以下是行向量和列向量的示例：

% Row vector with elements 1, 2, 3, 4
row_vector = [1, 2, 3, 4];

% Column vector with elements 5, 6, 7, 8
column_vector = [5; 6; 7; 8];

让我们使用函数来创建向量，如下所示：

% Creates a row vector of 10 linearly spaced points from 0 to 1
linear_vector = linspace(0, 1, 10);

% Row vector of 5 ones
ones_vector = ones(1, 5);

% Column vector of 4 zeros
zeros_vector = zeros(4, 1);

使用的函数是 linspace()、ones() 和 zeros()。

在 Matlab 中绘制向量

可以使用 quiver() 函数在 Matlab 中绘制向量。

语法

quiver(X,Y,U,V)
quiver(U,V)
quiver(___,scale)
quiver(___,LineSpec)

让我们详细了解每种语法。

quiver(X,Y,U,V) - MATLAB 中的 quiver(X,Y,U,V) 函数使用在特定笛卡尔坐标 X 和 Y 处的方向分量 U 和 V 生成箭头图。例如，每个箭头都从坐标 X(1)、Y(1) 开始，水平方向基于 U(1)，垂直方向基于 V(1)。默认情况下，quiver 会自动调整箭头长度以防止重叠。

quiver(U,V) - MATLAB 中的 quiver(U,V) 函数使用在均匀分布的位置处的方向分量 U 和 V 生成箭头图。当 U 和 V 是向量时，箭头的 x 坐标跨越从 1 到 U 和 V 中元素的数量，而它们的 y 坐标都设置为 1。如果 U 和 V 是矩阵，则箭头的 x 坐标跨越从 1 到 U 和 V 中的列数，而它们的 y 坐标范围从 1 到 U 和 V 中的行数。

quiver(___,scale) - MATLAB 中的 quiver(___, scale) 函数按以下方式修改箭头长度：

• 如果 scale 是正值，则该函数会自动调整箭头大小以防止重叠，然后按指定的比例因子缩放它们。例如，比例因子为 2 会使箭头长度加倍，而 0.5 会使箭头长度减半。
• 当 scale 设置为 'off' 或 0（例如，quiver(X,Y,U,V,'off')）时，自动缩放功能将被禁用，从而禁用箭头长度的自动调整。

quiver(___,LineSpec) - quiver(___, LineSpec) 函数配置绘图的线型、标记和颜色。标记位于 X 和 Y 指定的坐标处。当使用 LineSpec 指定标记时，不会显示箭头。要显示带有标记的箭头，最好单独设置 Marker 属性。

向量绘图示例

以下是一些向量绘图示例：

示例 1

在此示例中，X 和 Y 表示箭头开始的坐标。

U 和 V 表示方向分量，U 确定箭头的水平长度，V 确定箭头的垂直长度。

% Define coordinates and directional components
X = [1, 2, 3]; % X-coordinates
Y = [1, 1, 1]; % Y-coordinates
U = [2, -1, 3]; % Horizontal components
V = [3, 1, -2]; % Vertical components

% Plotting arrows using quiver

quiver(X, Y, U, V);

% Setting plot properties
xlabel('X-axis');
ylabel('Y-axis');
title('Arrow Plot using quiver');

让我们执行代码并检查输出：

示例 2

在此示例中，U_vector 和 V_vector 分别表示沿 x 轴和 y 轴的方向分量。

由于 U_vector 和 V_vector 都是向量，因此箭头的 x 坐标将跨越从 1 到向量中元素的数量，而所有箭头的 y 坐标都将设置为 1。

% Creating vectors U and V
U_vector = [1, 2, 3, 4]; % Directional components for x-axis
V_vector = [2, 1, 3, 2]; % Directional components for y-axis

% Plotting arrows using quiver with vectors
quiver(U_vector, V_vector);

% Setting plot properties
xlabel('X-axis');
ylabel('Y-axis');
title('Arrow Plot using quiver with Vectors');

执行后，输出如下：

示例 3

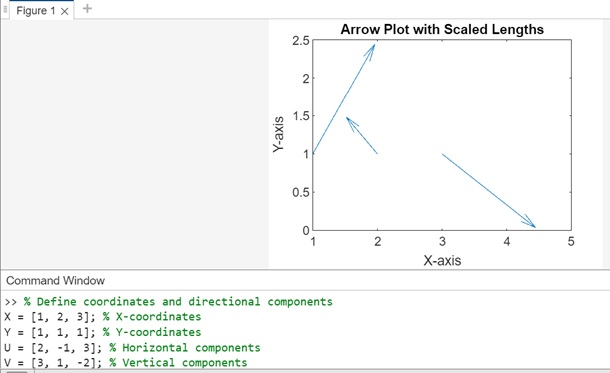
使用正值缩放图形。在此示例中，X、Y、U 和 V 定义坐标和方向分量。quiver 函数与比例因子 1.5 一起使用，该因子会自动调整和缩放箭头长度。

% Define coordinates and directional components
X = [1, 2, 3]; % X-coordinates
Y = [1, 1, 1]; % Y-coordinates
U = [2, -1, 3]; % Horizontal components
V = [3, 1, -2]; % Vertical components

% Plotting arrows with automatic scaling by a factor of 1.5

quiver(X, Y, U, V, 1.5);

% Setting plot properties
xlabel('X-axis');
ylabel('Y-axis');
title('Arrow Plot with Scaled Lengths');

执行后，输出为：

示例 4

此示例将演示 LineSpec 的用法。因此，X、Y、U 和 V 定义坐标和方向分量。quiver() 函数与 LineSpec 参数 'ro' 一起使用，该参数将红色圆圈设置为指定坐标处的标记，而不会显示箭头。

% Define coordinates and directional components
X = [1, 2, 3]; % X-coordinates
Y = [1, 1, 1]; % Y-coordinates
U = [2, -1, 3]; % Horizontal components
V = [3, 1, -2]; % Vertical components

% Plotting arrows with LineSpec to show markers without arrowheads
quiver(X, Y, U, V, 'ro'); % 'ro' sets red color and circles as markers

% Setting plot properties
xlabel('X-axis');
ylabel('Y-axis');
title('Arrow Plot with Markers using LineSpec');

执行后的输出为：