MATLAB - 微积分

MATLAB 提供多种方法来解决微积分问题，求解任意阶次的微分方程以及计算极限。最重要的是，您可以轻松绘制复杂函数的图形，并通过求解原函数及其导数来检查图形上的最大值、最小值和其他静止点。

本章将讨论微积分问题。本章将讨论预备微积分概念，即计算函数极限和验证极限的性质。

在下一章微分中，我们将计算表达式的导数，并在图形上找到局部最大值和最小值。我们还将讨论求解微分方程。

最后，在积分章节中，我们将讨论积分学。

计算极限

MATLAB 提供了limit函数用于计算极限。在其最基本的形式中，limit函数将表达式作为参数，并找到当自变量趋于零时表达式的极限。

例如，让我们计算函数 f(x) = (x³ + 5)/(x⁴ + 7) 在 x 趋于零时的极限。

syms x
limit((x^3 + 5)/(x^4 + 7))

MATLAB 将执行上述语句并返回以下结果：

ans =
   5/7

limit 函数属于符号计算的范畴；您需要使用syms函数来告诉 MATLAB 您正在使用哪些符号变量。您还可以计算函数的极限，当变量趋于某个非零数时。要计算 lim _x->a(f(x))，我们使用 limit 命令及其参数。第一个是表达式，第二个是 x 趋近的数字，这里它是 a。

例如，让我们计算函数 f(x) = (x-3)/(x-1) 在 x 趋于 1 时的极限。

limit((x - 3)/(x-1),1)

MATLAB 将执行上述语句并返回以下结果：

ans =
   NaN

让我们来看另一个例子：

limit(x^2 + 5, 3)

MATLAB 将执行上述语句并返回以下结果：

ans =
   14

使用 Octave 计算极限

以下是使用symbolic包的上述示例的 Octave 版本，尝试执行并比较结果：

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

Octave 将执行上述语句并返回以下结果：

ans =
   0.7142857142857142857

验证极限的基本性质

代数极限定理提供了一些极限的基本性质。这些性质如下：

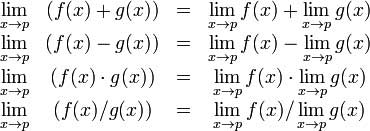
让我们考虑两个函数：

f(x) = (3x + 5)/(x - 3)
g(x) = x² + 1。

让我们计算这两个函数在 x 趋于 5 时的极限，并使用这两个函数和 MATLAB 验证极限的基本性质。

示例

创建一个脚本文件，并将以下代码输入其中：

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

运行该文件时，它将显示：

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

使用 Octave 验证极限的基本性质

以下是使用symbolic包的上述示例的 Octave 版本，尝试执行并比较结果：

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

Octave 将执行上述语句并返回以下结果：

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

左侧和右侧极限

当函数在变量的某个特定值处有不连续性时，该点的极限不存在。换句话说，当 x 从左侧逼近 a 时极限的值不等于 x 从右侧逼近 a 时极限的值时，函数 f(x) 在 x = a 处具有不连续性。

这导致了左极限和右极限的概念。左极限定义为 x 从左侧趋于 a 的极限，即 x 对于 x < a 的值逼近 a。右极限定义为 x 从右侧趋于 a 的极限，即 x 对于 x > a 的值逼近 a。当左极限和右极限不相等时，极限不存在。

让我们考虑一个函数：

f(x) = (x - 3)/|x - 3|

我们将证明 lim_x->3 f(x) 不存在。MATLAB 通过两种方式帮助我们确定这一事实：

通过绘制函数图形并显示不连续性。
通过计算极限并显示两者不同。

左极限和右极限是通过将字符字符串“left”和“right”作为最后一个参数传递给 limit 命令来计算的。

示例

创建一个脚本文件，并将以下代码输入其中：

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

运行该文件时，MATLAB 将绘制以下图形

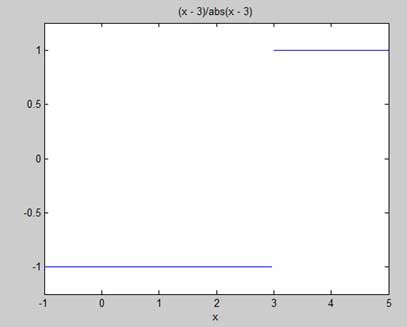
之后将显示以下输出：

l =
   -1
  
r =
   1

打印页面