MATLAB - 插值

上一页
下一页

插值是数学和计算机科学中使用的一种方法，用于估计已知数据点之间未知的值。它通常用于各个领域，包括信号处理、计算机图形学和数值分析，以创建平滑的曲线或曲面来近似数据。

在 MATLAB 中，插值是使用诸如 **interp1()**（用于一维插值）和 **interp2()**（用于二维插值）之类的函数实现的。这些函数采用已知数据点（x 和 y 坐标）以及需要进行插值的一组点。可以指定插值方法，例如线性插值（'linear'）、样条插值（'spline'）或最近邻插值（'nearest'）。所选方法决定了在已知数据点之间如何构建曲线或曲面。

通过使用插值，您可以填充缺失数据，创建更平滑的数据表示，并为可视化或分析生成新的数据点。MATLAB 的插值函数为处理未定期采样数据或从离散数据点生成插值曲面提供了强大的工具。

语法

y = interp(x,r)
y = interp(x,r,n,cutoff)
[y,b] = interp(x,r,n,cutoff)

上面提到的语法的解释如下：

**y = interp(x,r)** - 获取信号 x 并将其采样率提高 r 倍。

**y = interp(x,r,n,cutoff)** - 这里我们有两个新增内容，即 n 和 cutoff。n 是用于插值扩展信号的原始样本值数量的一半。

cutoff 是输入信号的归一化截止频率，指定为奈奎斯特频率的一部分。

**[y,b] = interp(x,r,n,cutoff)** - 返回用于插值的滤波器系数。

示例 1：使用 y = interp(x,r)

我们拥有的代码为：

x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
r = 2;
y = interp(x, r);
subplot(2, 1, 1);
stem(x, 'b', 'DisplayName', 'Original Signal');
xlabel('Sample');
ylabel('Value');
title('Original and Interpolated Signals');
legend('show');
subplot(2, 1, 2);
stem(y, 'r', 'DisplayName', 'Interpolated Signal');
xlabel('Sample');
ylabel('Value');
legend('show');

此代码创建一个带有两个图的子图：一个用于原始信号 (x)，另一个用于插值信号 (y)。stem 函数用于将信号绘制为茎状图，其中每个数据点都表示为一条垂直线。subplot(2, 1, 1) 命令将绘图区域划分为两行一列，并为原始信号选择第一个子图。subplot(2, 1, 2) 命令为插值信号选择第二个子图。

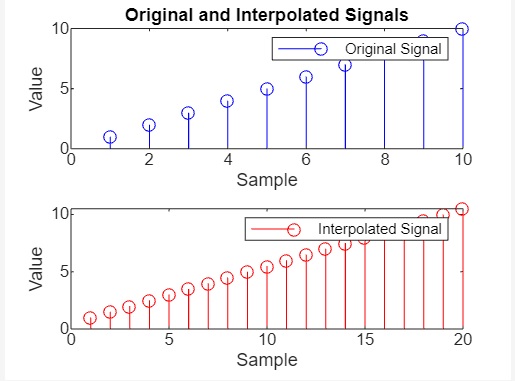
interpolated signal

示例 2：使用其他参数（如 n 和 cutoff）对信号进行插值

我们拥有的代码为：

n = 5;
x = 1:20;
r = 2;
cutoff = 0.5;
y = interp(x, r, n, cutoff);
subplot(2, 1, 1);
stem(x, 'b', 'DisplayName', 'Original Signal');
xlabel('Sample');
ylabel('Value');
title('Original and Interpolated Signals');
legend('show');

subplot(2, 1, 2);
stem(y, 'r', 'DisplayName', 'Interpolated Signal');
xlabel('Sample');
ylabel('Value');
legend('show');

在上面的示例中：

  • 滤波器长度 n 设置为 5，它确定用于插值的滤波器的长度。它是用于插值扩展信号的原始样本值数量的一半。原始信号 x 定义为 1:20，它创建一个从 1 到 20 的整数向量。
  • 采样率提高了 2 倍，由 r = 2 指定。归一化截止频率 cutoff 设置为 0.5，它是奈奎斯特频率的一部分。它确定滤波器衰减到一半功率的频率。
  • interp() 函数用于使用指定参数 (r、n、cutoff) 对原始信号 x 进行插值。插值过程提高了原始信号的采样率，从而产生新的插值信号 y。
  • 使用 subplot() 函数创建两个子图以显示原始信号和插值信号。stem() 函数用于将信号绘制为茎状图，其中每个数据点都表示为一条垂直线。第一个子图以蓝色显示原始信号 (x)，第二个子图以红色显示插值信号 (y)。x 轴表示样本编号，y 轴表示信号值。

当代码在 matlab 命令窗口中执行时，输出为：

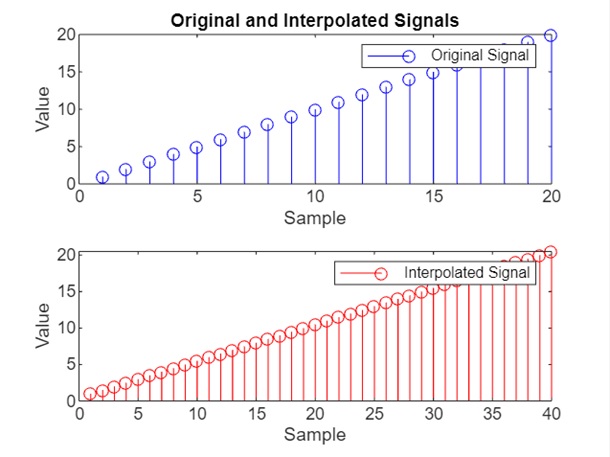
Signal additional parameters

示例 3：使用 [y,b] = interp(x,r,n,cutoff) 显示滤波器系数

我们拥有的代码为：

x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12];
r = 2;
n = 5;
cutoff = 0.5;
[y, b] = interp(x, r, n, cutoff);

% Plot the original and interpolated signals
subplot(2, 1, 1);
stem(x, 'b', 'DisplayName', 'Original Signal');
xlabel('Sample');
ylabel('Value');
title('Original and Interpolated Signals');
legend('show');

subplot(2, 1, 2);
stem(y, 'r', 'DisplayName', 'Interpolated Signal');
xlabel('Sample');
ylabel('Value');
legend('show');

% Display the filter coefficients
disp('Filter Coefficients:');
disp(b);

在此示例中，interp() 函数用于使用指定参数 (r、n、cutoff) 对原始信号 x 进行插值。获得插值信号 y，并且还返回用于插值的滤波器系数 b。在示例的末尾使用 disp(b) 显示滤波器系数。

当代码执行时，输出如下：

Filter Coefficients:
    0.0000
    0.0020
   -0.0000
   -0.0135
    0.0000
    0.0511
   -0.0000
   -0.1546
    0.0000
    0.6150
    1.0000
    0.6150
    0.0000
   -0.1546
   -0.0000
    0.0511
    0.0000
   -0.0135
   -0.0000
    0.0020
    0.0000
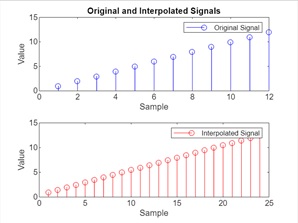
filter coefficients

对网格数据进行插值

处理网格数据时，插值通常用于估计网格点之间的值。MATLAB 提供了多个用于插值网格数据的函数，例如 interp2（用于二维数据）和 interp3（用于三维数据）。这些函数可用于创建更平滑的数据表示或提取网格内特定点的值。

示例 1：使用 interp2 对二维网格数据进行插值

我们拥有的代码为：

[x, y] = meshgrid(-2:0.5:2, -2:0.5:2);

% Define the function z = f(x, y) = x^2 + y^2
z = x.^2 + y.^2;

% Create a finer grid for interpolation
[xq, yq] = meshgrid(-2:0.1:2, -2:0.1:2);

% Perform 2D interpolation
zq = interp2(x, y, z, xq, yq, 'cubic');

% Plot the original and interpolated data
figure;
surf(x, y, z);
hold on;
surf(xq, yq, zq);
legend('Original Data', 'Interpolated Data');
xlabel('X');
ylabel('Y');
zlabel('Z');
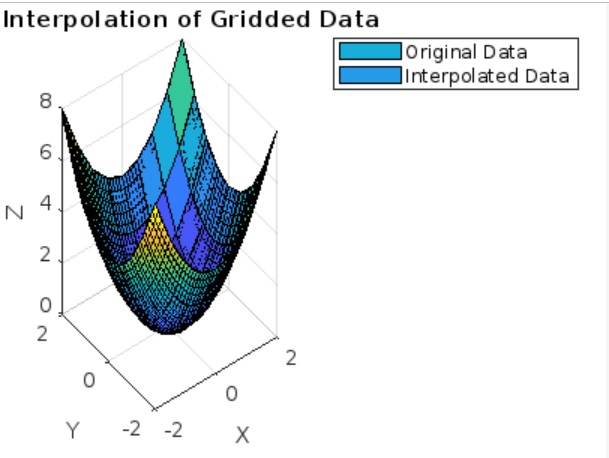
title('2D Interpolation of Gridded Data');

在此示例中，我们首先使用 meshgrid 创建 x 和 y 值的网格。然后，我们定义一个函数 z = f(x, y) = x^2 + y^2 并计算网格上相应的 z 值。接下来，我们使用 meshgrid 再次创建一个用于插值的更精细的网格。最后，我们使用 interp2 和三次方法对新网格点 xq 和 yq 处的 z 值进行插值。然后将插值数据与原始数据一起绘制以进行比较。

执行后，输出为：

2d gridded data

示例 2：使用 interp3 对三维网格数据进行插值

我们拥有的代码为：

[x, y, z] = meshgrid(-2:0.5:2, -2:0.5:2, -2:0.5:2);


w = x.^2 + y.^2 + z.^2;

% Create a finer grid for interpolation
[xq, yq, zq] = meshgrid(-2:0.1:2, -2:0.1:2, -2:0.1:2);

% Perform 3D interpolation
wq = interp3(x, y, z, w, xq, yq, zq, 'cubic');

% Plot the original and interpolated data
figure;
slice(x, y, z, w, [0], [0], [0]); % plot slices of the original data
hold on;
slice(xq, yq, zq, wq, [0], [0], [0]); % plot slices of the interpolated data
xlabel('X');
ylabel('Y');
zlabel('Z');
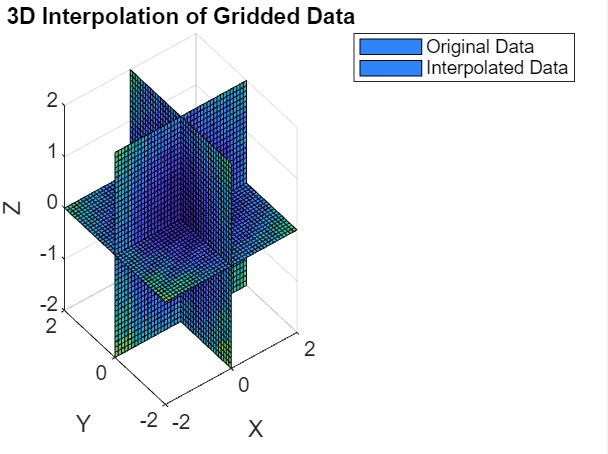
title('3D Interpolation of Gridded Data');
legend('Original Data', 'Interpolated Data');

在此示例中，我们首先使用 meshgrid 创建 x、y 和 z 值的网格。然后，我们定义一个函数 w = f(x, y, z) = x^2 + y^2 + z^2 并计算网格上相应的 w 值。接下来，我们使用 meshgrid 再次创建一个用于插值的更精细的网格。最后，我们使用 interp3 和三次方法对新网格点 xq、yq 和 zq 处的 w 值进行插值。然后将插值数据与原始数据一起绘制以进行比较。

执行后，我们有：

3d gridded data

对离散数据进行插值

MATLAB 中的散点数据是指未按规则网格排列的一组数据点。这种类型的数据在许多科学和工程应用中很常见，在这些应用中，测量是在任意位置进行的。散点数据插值涉及估计这些点之间的值，以创建平滑的表面或函数。

在 MATLAB 中，griddata 函数通常用于插值散点数据。它使用各种插值方法，例如线性、最近邻、三次和样条，来估计数据集中未明确给出的点的值。

示例

我们拥有的代码为：

x = rand(100,1)*4 - 2;
y = rand(100,1)*4 - 2;
z = peaks(x,y);

% Define a regular grid for interpolation
[Xq,Yq] = meshgrid(-2:0.1:2, -2:0.1:2);

% Interpolate scattered data to the regular grid using griddata
Zq = griddata(x,y,z,Xq,Yq,'cubic');

% Plot the scattered data and the interpolated surface
figure;
scatter3(x, y, z, 'filled'); % Plot scattered data points
hold on;
surf(Xq, Yq, Zq); % Plot interpolated surface
hold off;
xlabel('X');
ylabel('Y');
zlabel('Z');
title('Interpolating Scattered Data');
legend('Scattered Data', 'Interpolated Surface');

在示例中 -

  • 我们生成随机散点数据点 (x, y) 并使用 peaks 函数计算相应的 z 值。
  • 我们使用 meshgrid 在与散点数据相同的范围内定义规则网格 (Xq, Yq)。
  • 我们使用 griddata 将散点数据插值到规则网格上。插值使用 'cubic' 方法，但您也可以使用 'linear'、'nearest' 或其他方法。
  • 最后，我们绘制散点数据点和插值表面以可视化插值。

执行后的输出为 -

interpolating scattered data
打印页面
上一页
下一页
广告